Методы линейного программирования

При решении ряда задач планово-производственного характера (определение оптимального распределения одного вида сырья между несколькими производствами предприятия, получение продуктов различной сортности, учет потребностей рынка, задачи компаундирования продуктов, задачи об оптимальных маршрутах транспортных перевозок сырья и продукции и др.) целевая функция часто формируется в виде линейной функции, представляющей собой бесконечную плоскость в многомерном пространстве параметров задачи 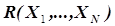. Естественно, в этом случае целевая функция не имеет экстремума и для решения задачи вводится ряд ограничений в области исследования задачи на оптимум. Эти ограничения обычно выражаются в форме неравенств, которые «вырезают» в области исследования область принципиальной реализации процесса с учетом ограничений. Неравенства могут носить как линейный, так и нелинейный характер. В первом случае область принципиальной реализации процесса в пространстве 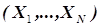представляет собой многоугольник, при наличии нелинейных ограничений соответствующие им стороны многоугольника имеют вид дуг (рис.5.7).

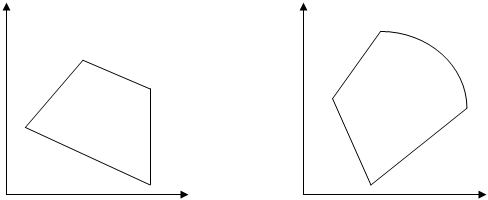
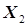
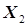
Область принципиальной реализации процесса

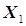
а б

Рис.5.7. Формирование области принципиальной реализации двухпараметрического процесса с учетом линейных. ограничений (а)

и с наличием кроме линейных и нелинейного ограничения (б)

Проекция области принципиальной реализации процесса на поверхность целевой функции 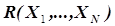«вырезает» в ней область реализуемых значений критерия оптимальности (рис. 5.8).

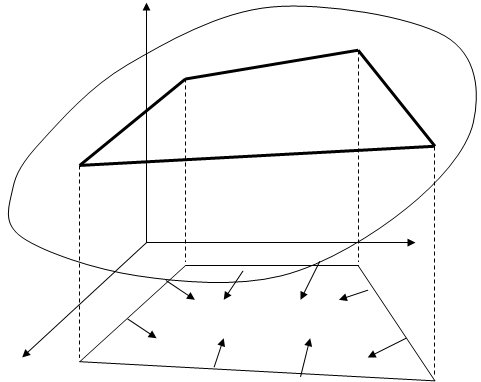Область

реализуемых значений

критерия оптимальности

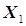
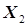
Рис. 5.8. Формирование области реализуемых значений

критерия оптимальности для двух параметрического процесса.

В силу линейности области реализуемых значений критерия оптимальности, величина критерия оптимальности в ней изменяется монотонно и линейно и по каждой из линий ограничения этой области критерий растет или уменьшается равномерно, таким образом в одной из двух узловых точек линии ограничения (точек, получающихся при пересечении разных ограничений) критерий 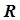будет самым большим для данной линии ограничения, а во второй точке – минимальным. Таким образом для нахождения наибольшего значения критерия оптимальности необходимо рассчитать его значения во всех узловых точках, образующихся пересечением всех линий ограничений в области реализуемых значений критерия оптимальности. Для определения координат узловых точек необходимо решить все варианты систем уравнений, состоящих из двух различных ограничений задачи. При наличии нелинейных ограничений необходимо исследовать соответствующую дугу ограничения на поверхности 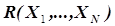на наличие экстремума одним из методов нелинейного программирования.

В качестве примера решения задач оптимизации с использованием метода нелинейного программирования рассмотрим расчет производственной программы группы установок

На предприятии на двух установках получают продукты А и В в количестве 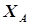и , причем прибыль от их реализации и –различны, например, на нефтеперерабатывающем заводе на установке первичной переработки нефти (АВТ) вырабатывают фракции дешевого бензина А, а на установке облагораживания бензина часть бензина с уста-новки АВТ подвергается переработке с получением фракций более дорогого высокооктанового бензина В. При этом на работу установок первичной переработки нефти и облагораживания бензина накладывается ряд ограничений 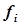типа неравенств. Сформулируем несколько подобных ограничений типа 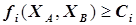и 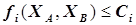, где. 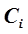– конкретное ограничение.

Первая группа ограничений на рабочую производительность по товарному продукту, накладывается на каждую из установок в соответствии с проектными характеристиками аппаратов, например:

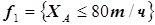
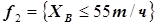. (5.38)

Вторая группа ограничений на допустимую минимальную производительность по товарному продукту, накладывается на каждую из установок в соответствии с проектными характеристиками аппаратов, например:

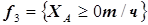(5.39)

.

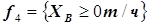Характерным ограничением является также ограничение на выпуск совместной продукции (бензина), связанное с тем, что часть бензина с установки первичной переработки нефти является сырьем установки облагораживания бензина, например:

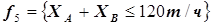. (5.40)

Необходимым условием оптимизации ассортимента продукции является ограничение по конъюнктурным условиям рынка – на планируемый период работы установок прогнозируется соотношение между потребностью в бензинах марок А и В, например:

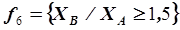. (5.41)

Целевая функция имеет вид

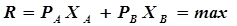, (5.42)

где – критерий оптимальности, характеризующий максимальную прибыль, которую ожидается получить от реализации оптимального ассортимента продукции, руб./ч.

Поскольку целевая функция – плоскость, не имеющая экстремума, то решение задачи выполняется методом линейного программирования. В результате пересечения целевой функции с шестью функциями ограничений () на плоскости 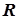выделяется замкнутая область исследования задачи (рис. 5.9), в которой 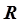принимает наибольшее значение, которое находится в одной из узловых точек границы области исследования (узловая точка – точка пересечения двух ограничений и плоскости ).

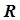Сопоставляя значения 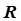в узловых точках, находим искомое решение задачи. Для удобства анализа графического решения задачи на рис. 5.9,б нанесены линии равного уровня (пунктирные линии), для которых значение 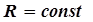при различных значениях 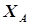и рассчитывается по уравнению (5.42); при расчете линий равного уровня принята прибыль от реализации для бензина марки А =1000 руб./т, =1300 руб./т. При изменении ценовой политики в экономике, курса рубля и, соответственно, абсолютной прибыли угол наклона пунктирных линий равного уровня будет изменяться незначительно, а существенно будет изменяться величина 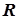для соответствующей линии равного уровня.

Область реализации процесса на рис. 5.9 залита серым цветом.

Х_А, т/ч

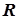=130000 руб./ч

120––8

9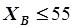

()

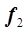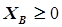
80 2 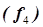5 4 11

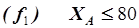
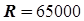р/ч

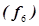
1 3 10

40 ––

9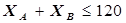

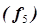
1 3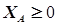

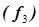
(12,13)

Х_А 0 20 40 60 80 100 120

Х_В, т/ч

а б

Рис. 5.9. Пространственная (а) и плоскостная (б) иллюстрация

решения задачи методом линейного программирования

На рис. 5.9 черными точками отмечены точки пересечения функций ограничения:

точка 1 – 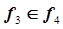, точка 5 – 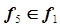, точка 10 – ,

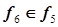точка 2 – 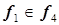, точка 6 – 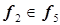, точка 11 – ,

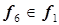точка 3 – 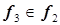, точка 7 – 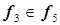, точка 12 – ,

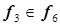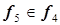точка 4 – , точка 8 – , точка 13 – ,

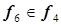точка 9 –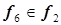

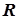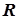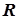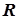белыми точками (точки 1 , 3 и 9) отмечены узловые точки границы области оптимизации задачи. Как наглядно видно из рис. 5.9,б, по любой граничной линии, соединяющей две узловые точки, происходит монотонное изменение критерия оптимальности , поэтом для решения задачи достаточно сопоставить значения в узловых точках ₁, ₃, 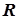₉; поскольку 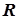₁=0, 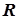₃= 71500 руб./ч, 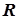₉;=108400 руб./ч, то точка 9 с координатами Х_А = 36,9 т/ч и Х_В = 55т/ч является наилучшей.

Расчет задачи на ЭВМ сводится к последовательному попарному решению уравнений ограничения на базе уравнений (5.38) – (5.42) с расчетом координат Х₁ (М) и Х₂ (М) очередной М -ой точки решением системы уравнений (Х₁ =Х_А и Х₂ =Х_В)

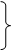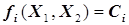
. (5.43)

Число узловых точек М, как результат попарного решения уравнений ограничений, может быть рассчитано как

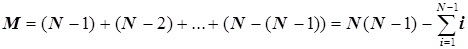. (5.44)

Систему уравнений (5.43) для компьютерного расчета удобно представить в форме

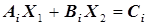
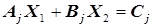(5.45)

с вводом массивов коэффициентов 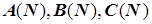для 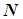функций ограничений в исходные данные задачи. В общем случае систему (5.45) можно решить методом Гаусса, в случае двумерной задачи для расчета координат Х₁ (М) и Х₂ (М) точки пересечения 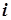-го и 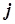-го ограничений можно воспользоваться уравнениями

Х₁ (М)= (5.46)

и

Х₂ (М)= 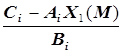. (5.47)

После расчета координат корня системы уравнений (5.45) по ограничениям 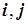необходимо проверить, удовлетворяет ли данная точка условиям всех остальных функций ограничений. Если расчетная узловая точка подчиняется всем ограничениям, то эта точка находится на границе области оптимизации. Для упрощения блок-схемы расчета (рис. 5.10) в ней рассмотрен только анализ ограничений вида .

При наличии дополнительно 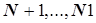ограничений типа 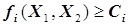(например, 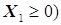следует дополнить блок схему фраг-ментом, аналогичным выделенным штриховой линией фрагменту продол-жения рис.5.10 с заменой знака в блоке сравнения 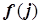и 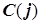. Для каждой узловой 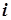-й точки, удовлетворяющей всем ограничениям, рассчитывается значение критерия 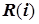и определяется оптимальная точка решения.