Методы динамического программирования

Эта группа методов наиболее широко используется для оптимизации многостадийных процессов, когда ставится задача оптимизации всей системы в целом. Метод предусматривает разбивку исследуемого процесса во времени или пространстве на отдельные ступени или стадии. В качестве подобного подхода к решению задачи можно привести условную разбивку слоя катализатора на отдельные участки при расчете каталитических процессов. При оптимизации работы технологической установки в качестве отдельных ступеней можно выбирать единичный элемент оборудования (тарелка в ректификационной колонне, колонна в блока ректификационных колонн, реактор в каскаде реакторов).

Специфика работы сложных химико-технологических систем (ХТС) заключается в том, что оптимальная работа каждого из аппаратов системы не означает оптимальной работы всей системы в целом. И наоборот – при оптимальной работе ХТС отдельные ее аппараты могут работать в неоптимальном режиме с позиций выбранного для всей системы единого критерия оптимальности.

Задача динамического программирования в общем случае сводится к определению такого оптимального управления на i -й ступени ХТС, чтобы совокупность всех последующих ступеней работала в оптимальном режиме. В одном из наиболее часто применяемых методов динамического программирования – методе Беллмана – эта задачи решается в два этапа.

Начало

Ввод 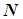функций ограничений

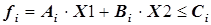
в форме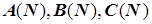

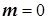
1

нет да

нет нет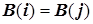

да 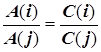да

да 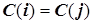нет

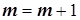нет да

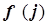и – и –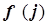

тождественны параллельны

Рис.5.10. Принципиальная блок-схема решения примера о разработке производственной программы группы установок методом линейного

программирования для ограничений типа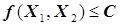

1

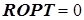Расчет 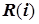по (3.55)

нет

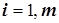
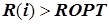
да

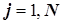
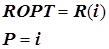
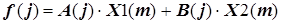
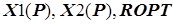
да нет

Конец

Продолжение рис. 5.10

На первом этапе формируется целевая функция в виде рекуррентного соотношения для i -й ступени ХТС, включающей N ступеней, начиная от завершающей N- й ступени (тогда i -я ступень приобретает вторую нумерацию и имеет номер N -(i -1):

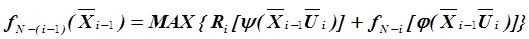, (5.48)

где 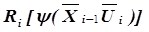–целевая функция i -й ступени;

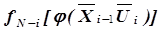– обобщенная целевая функция для всех следующих ступеней вплоть до последней включительно; 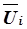– вектор параметров управления i -й ступенью ХТС; 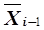– вектор параметров входа в i -ю ступень, совпадающий с вектором параметров выхода предыдущей i –1 ступени.

В конкретном случае величина критерия оптимальности 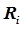может не только максимизировать процесс, как это записано в (5.48), но и минимизировать его.

После разработки формализованной оптимизации всей ХТС, пройдя от конца ХТС к ее началу на основе уравнения (5.48), получают математическую модель оптимизации ХТС с разработкой уравнений, связывающий вектор оптимальных параметров управления 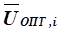на i –й ступени такой, что весь комплекс ступени от i –й до последней будет работать оптимально при любых значениях вектора входных параметров

i –й ступени .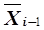

На втором этапе расчета, зная начальные условия ведения процесса и набор уравнений для расчета оптимальных параметров управления, рассчитывают всю ХТС по ступеням от начала к концу, определяя все параметры векторов 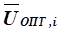, 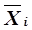и критерии оптимальности .

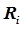В силу определенной сложности восприятия метода динамического программирования, проанализируем методику его применения на примере оптимизации каскада реакторов идеального смешения- характерного аппаратурного оформления ряда процессов химической технологии.

При проектировании каскада из 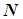реакторов идеального смешения для проведения химической реакции 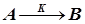первого порядка в изотермических стационарных условиях поставлена задача минимизации капитальных затрат на сооружение реакторного блока.

Исходные данные расчета: расход исходного сырья 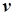, начальная концентрация компонента А в сырье С_А0, его конечная концентрация на выходе из реакторного блока С_АК, число ступеней каскада 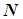, константа скорости реакции К – известны.

Очевидно, что минимум капитальных затрат на сооружение реакторного блока эквивалентен минимуму объема реакторов блока, в котором каждый 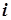-й блок (рис. 5.10) представляет собой ступень процесса.

С_{А, 0} 1

С_{А, 1} 2

●●●

С_{А, 2} С_{А, i-1} С_Аii

●●●

N С_{А, N-2}

С_{А, N-1} N -1

С_{А, N}

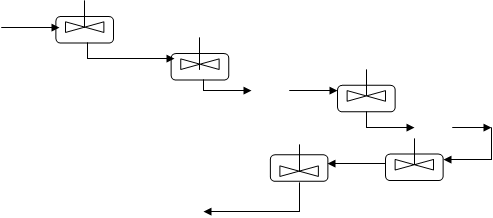
Рис. 5.10. Схема каскада реакторов

Задача оптимизации решается в два этапа. На первом этапе выполняют разработку математического описания задачи оптимизации объекта, рассматривая его работу последовательно от конца процесса к его началу.

Поскольку в данном примере во всех ступенях каскада используется одинаковое аппаратурное оформление (реактор идеального смешения), то можно ограничиться составлением математической модели для произвольной 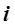-й ступени ( 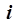-го блока) каскада, справедливой для всех остальных ступеней.

Исходя из общего вида полной математической модели реактора идеального смешения применительно к рассматриваемой конкретной реакции

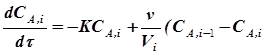), (5.49)

где 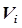– объем 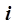-го блока каскада,

получим для стационарного режима работы системы целевую функцию для 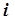-го блока в виде

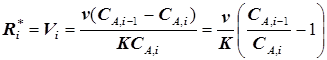(5.50)

или

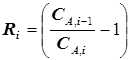, (5.51)

где 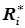– критерий оптимальности для 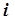-го блока, эквивалентный (пропорциональный) минимуму капитальных затрат на сооружение реактора объемом ;

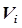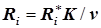– частный условный безразмерный критерий оптимальности, позволяющий устранить из дальнейших расчетов параметры 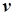и К и, таким образом, упростить расчеты и формируемые модели оптимизации.

Функция оптимизации для произвольного 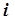-го блока (ступени процесса) формируется согласно уравнения (5.48) в общем виде как

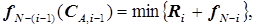(5.52)

где

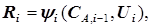(5.53)

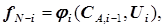(5.54)

где 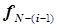– целевая функция, оптимизирующая работу данной 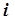-й ступени совокупно со всеми последующими ступенями;

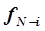– целевая функция, оптимизирующая работу всех последующих ступеней;

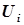– параметр управления 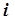-й ступенью, величина которого обеспечивает оптимальное функционирование 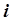-й и всех последующих ступеней.

1. Первый этап решения задачи.

1.1. Расчет последней пятой (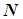 -ой) ступени.

Уравнение (5.49) для 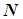-ой ступени примет вид ()

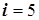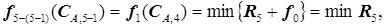(5.55)

поскольку за последней ступенью никаких оптимизируемых блоков нет.

Для 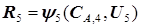воспользуемся уравнением (5.51), тогда

, (5.56)

где С_{А, 5} = С_{A, i} выступает какпараметр «управления» величиной объема реактора 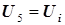в ходе проектирования каскада реакторов, поскольку для изотермического реактора идеального смешения объем конкретного реактора при прочих равных условиях определяется («управляется») принятой величиной концентрации веществ на выходе из реактора.

Очевидно, что для последней 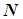-ой ступени каскада при заданном С_{А, К} объем реактора 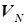будет иметь конкретную оптимальную величину при любой концентрации компонента А на входе в эту ступень С_А,4. Окончательно целевая функция 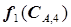и функция управления 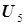будут иметь вид:

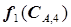
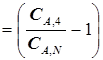, (5.57)

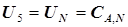(5.58)

и заносятся в итоговую табл. 5.2 для формирования полной модели оптимизации каскада реакторов.

1.2. Расчет предпоследней четвертой (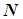 –1) ступени.

По аналогии с расчетом 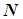-ой ступени

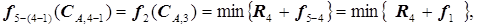(5.59)

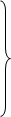
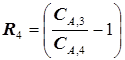
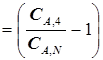, (5.60)

тогда уравнение (5.59) примет вид

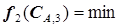
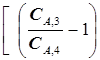
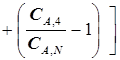. (5.61)

Ищем такое оптимальное управление 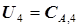, при котором при любых концентрациях компонента А на входе в четвертый реактор целевая функция (5.61) имеет минимум; взяв производную :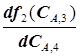

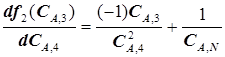=0, (5.62)

получим выражение для расчета оптимального управления четвертой ступенью

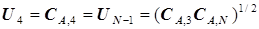; (5.63)

подстановка 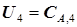в уравнение (5.61) позволяет упростить его запись:

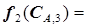
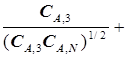
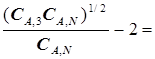
=2 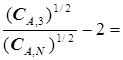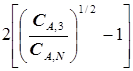. (5.64)

Итоги расчетов заносятся в табл. 3.2 для формирования полной модели оптимизации каскада реакторов.

1.3. Расчет третьей ступени каскада

По аналогии с предыдущим расчетом

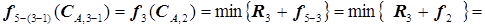
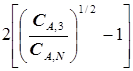
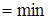= . (5.65)

Ищем такое оптимальное управление 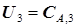, при котором при любых концентрациях компонента А на входе в третий реактор 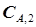целевая функция (5.65) имеет минимум; взяв производную :

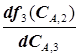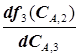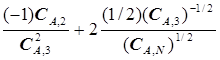= =0, (5.66)

получим выражение для расчета оптимального управления третьей ступенью

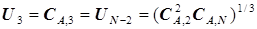; (5.67)

подстановка 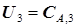в виде (5.67) в уравнение (5.65) позволяет упростить запись целевой функции, обеспечивающей оптимизацию совместно третьей, четвертой и пятой ступеней каскада:

=

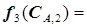
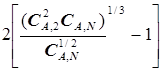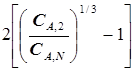= . (5.68)

Итоги расчетов заносятся в табл. 3.2 для формирования полной модели оптимизации каскада реакторов.

Анализ результатов расчета, внесенных в табл. 3.2, позволяет уже после расчета третьей ступени обнаружить закономерности в записи формул целевой функции 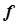и функции управления 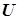, особенно если учесть, что 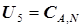можно рассмотреть и в форме

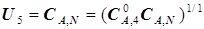. (5.69)

Как видно из табл. 5.2, при сохранении формы записи уравнений для расчета 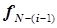и 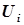в этих уравнениях монотонно изменяются показатели степеней, что позволяет записать уравнения для формирования 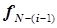и для дальнейших расчетов первого этапа без аналитического расчета второй и первой ступеней каскада.

Таблица 5.2