Вариационные процедуры можно применять и для объективного анализа, т.е интерполяции значений измерений в узлы модельной сетки при условии минимизации отклонения результатов анализа, как от фонового состояния (нормы), так и от результатов измерений [11]. В этом случае можно поставить задачу минимизации функционала качества в виде
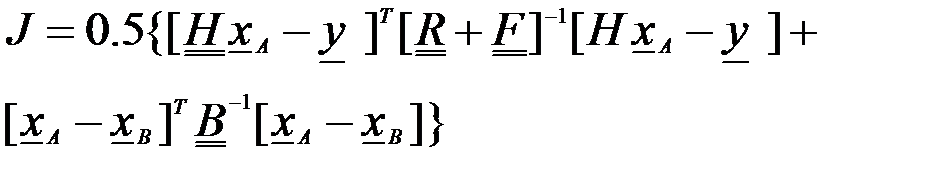 ,
,
где 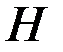 представляет оператор наблюдений и предназначен для представления (интерполирования) результатов с модельной сетки в точки наблюдений,
представляет оператор наблюдений и предназначен для представления (интерполирования) результатов с модельной сетки в точки наблюдений,
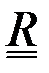 - матрица ковариаций ошибок наблюдений,
- матрица ковариаций ошибок наблюдений,
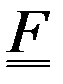 - матрица ошибок прямой задачи (интерполяции в точки наблюдений),
- матрица ошибок прямой задачи (интерполяции в точки наблюдений),
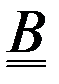 - матрица ковариаций ошибок представления фонового состояния (нормы).
- матрица ковариаций ошибок представления фонового состояния (нормы).
Задача нахождения оптимальных весов подразумевает минимизацию ошибок анализа, однако т.к. мы не знаем точных значений, то мы можем говорить, во-первых, только о статистических величинах, а, во-вторых, о вероятном распределении ошибок измерений, моделирования и оценки фонового состояния. Соответственно, можно ставить задачу об оценке вероятности нахождения величины 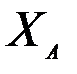 при заданных значениях
при заданных значениях 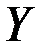 . Оптимальный анализ должен соответствовать максимальной вероятности того, что ошибки анализа минимальны. В большинстве случаев ошибки оценивания фонового состояния (моделирования) и измерений являются независимыми. В этом случае общая вероятность записывается как произведение вероятностей:
. Оптимальный анализ должен соответствовать максимальной вероятности того, что ошибки анализа минимальны. В большинстве случаев ошибки оценивания фонового состояния (моделирования) и измерений являются независимыми. В этом случае общая вероятность записывается как произведение вероятностей:
|
|
|
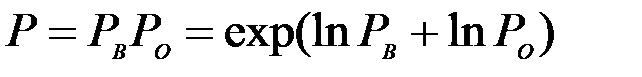 .
.
Вероятность того, что ошибки минимальны, будет максимальной, когда показатель экспоненты максимален, или минимальна обратная функция, которую называют функционалом качества:
 .
.
Если дополнительные ограничения накладываются на процесс ассимиляции, например моделирование и инициализация, то дополнительные слагаемые появляются в функционале качества: 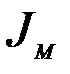 и
и 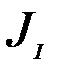 .
.
Если плотность вероятности распределения ошибок носит нормальный (Гауссовский) характер, то
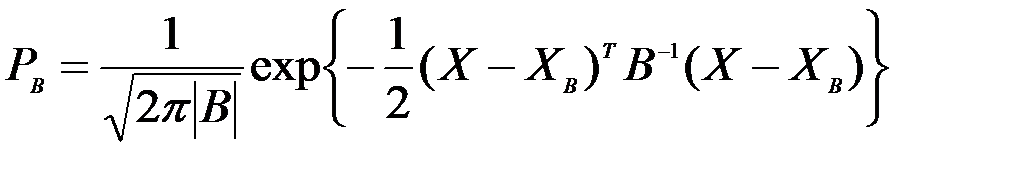 ,
,
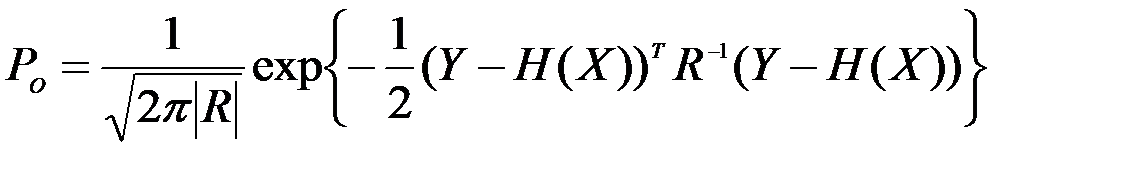 .
.
Тогда функционал качества имеет вид

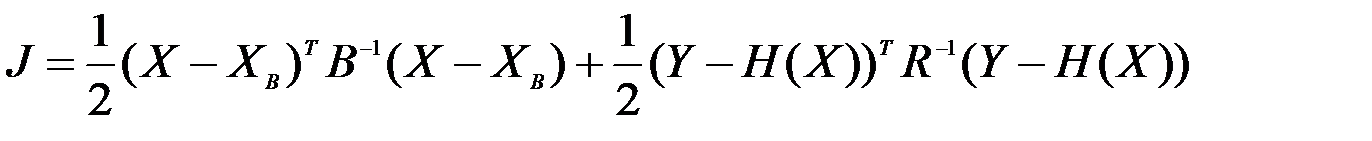 .
.
Таким образом, необходимость минимизировать функционал, содержащий функции распределения, которые, как правило, не известны, свелась к задаче минимизации функционала, содержащего только ковариации, что проще. Кроме того, если оператор наблюдений 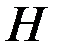 линеен, то функционал качества становится квадратичным по отношению к
линеен, то функционал качества становится квадратичным по отношению к 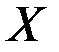 , который имеет только один минимум, что упрощает анализ. В-третьих, можно использовать известные эффективные алгоритмы минимизации квадратичных функционалов.
, который имеет только один минимум, что упрощает анализ. В-третьих, можно использовать известные эффективные алгоритмы минимизации квадратичных функционалов.
Можно минимизировать этот функционал одним из классических методов функционального анализа, например, методом Эйлера-Лагранжа, что приведет нас к сложным вычислениям.
С другой стороны можно идти по пути линеаризации и решать линейную задачу. Минимизация функционала качества по отношению к 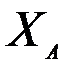 приводит к уравнению
приводит к уравнению
|
|
|
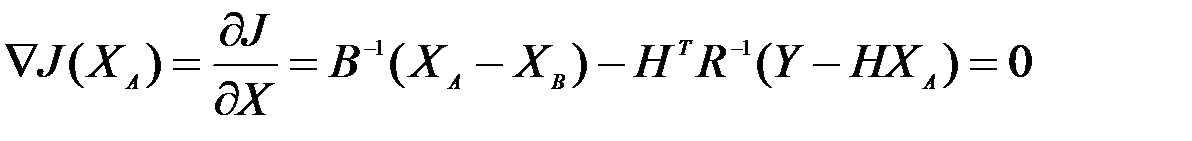 .
.
Оператор наблюдений 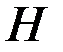 применяется не к
применяется не к 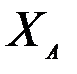 , а к
, а к 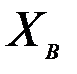 . Чтобы получить это, добавим и вычтем
. Чтобы получить это, добавим и вычтем 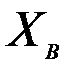 под оператором
под оператором 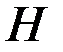 :
:
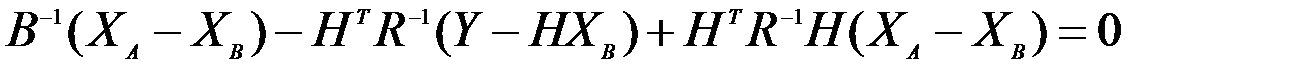 .
.
Откуда
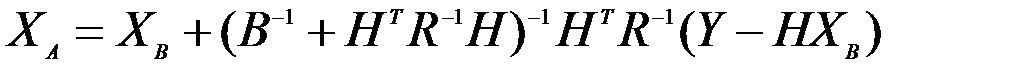 .
.
Рассмотрим теперь скобку 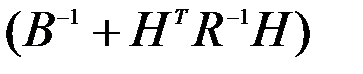 и умножим ее на
и умножим ее на 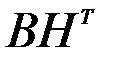 .
.
В результате получим
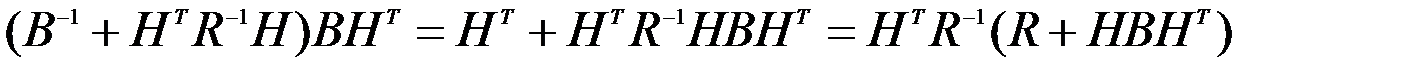 .
. 
Таким образом,
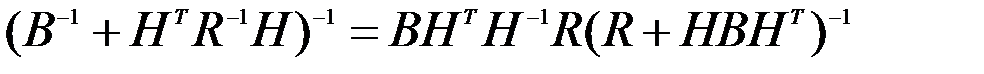 .
.
Подставляя в уравнение для 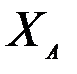 , имеем
, имеем
 .
.
Таким образом, из рассмотрения подхода максимума вероятности получили выражение аналогичное алгоритму оптимальной интерполяции, только без явного выражения матрицы весов 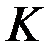 . Принципиальное отличие вариационных методов от оптимальной интерполяции заключается в том, что контрольными параметрами, к которым применяется метод минимизации, являются не веса, а сами искомые функции анализа.
. Принципиальное отличие вариационных методов от оптимальной интерполяции заключается в том, что контрольными параметрами, к которым применяется метод минимизации, являются не веса, а сами искомые функции анализа.
Рассмотрим альтернативный подход. Если, в общем случае оператор наблюдений не линеен, то сначала линеаризуем его около фонового состояния 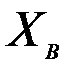 :
:
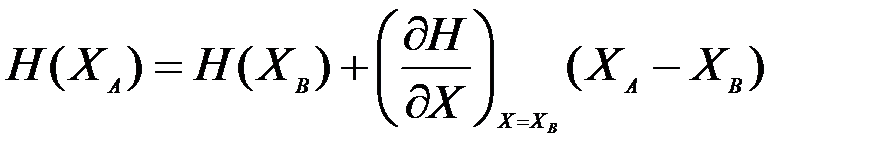
Если теперь в уравнение минимизации функционала качества подставить это линеаризованное значение для некоего текущего значения 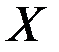 не равного
не равного 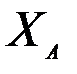 , то это уравнение даст значение для градиента, отличное от нуля:
, то это уравнение даст значение для градиента, отличное от нуля:
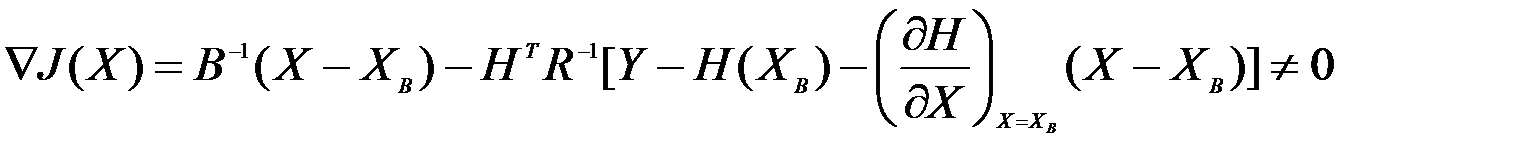 .
.
Здесь выражение 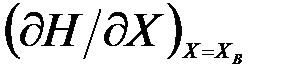 представляет собой так называемый Якобиан, или матрицу Якоби.
представляет собой так называемый Якобиан, или матрицу Якоби.
Для минимизации этого функционала можно применить итерационную процедуру последовательного уменьшения функционала 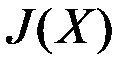 до достижения минимального значения (метод наискорейшего спуска).
до достижения минимального значения (метод наискорейшего спуска).
Определим следующую итерационную процедуру:
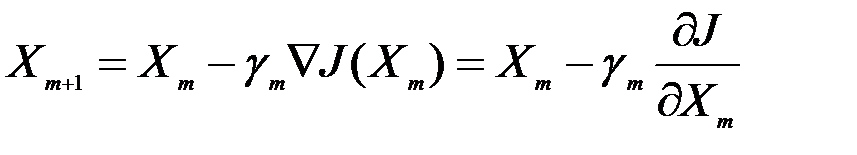 .
.
В качестве нулевой итерации  можно использовать фоновые значения
можно использовать фоновые значения  .
.
Рассмотрим одномерный пример.
Рассмотрим теперь функцию качества, зависящую от двух параметров
В общем случае 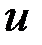 и
и 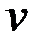 зависят от пространственных координат и времени, но в этом примере мы полагаем, что они определены в одной точке. На плоскости
зависят от пространственных координат и времени, но в этом примере мы полагаем, что они определены в одной точке. На плоскости 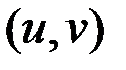 линии постоянных значений
линии постоянных значений  представляют собой эллипсы с осями
представляют собой эллипсы с осями 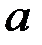 и
и 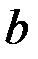 :
:
Градиент  в каждой точке этого пространства может быть определен как
в каждой точке этого пространства может быть определен как
В нашем случае градиент представляет собой вектор размерности 2 с элементами Вариации
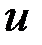 и
и 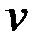 вызывают вариации функционала качества
вызывают вариации функционала качества , где
, а
. Стартуем с точки
. Если сделать малые изменения в
, то изменения в функционале качества будут
Задача стоит минимизировать  . В нашем случае задача имеет тривиальное решение – функционал достигает минимума равного нуля, когда
. В нашем случае задача имеет тривиальное решение – функционал достигает минимума равного нуля, когда 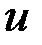 и
и 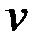 равны нулю.
равны нулю.
Посмотрим, как достичь этого решения методом наискорейшего спуска. Очевидно, что, если градиент положителен, функционал будет увеличиваться, если градиент отрицателен, то функционал будет уменьшаться. Нам нужно достичь минимума, поэтому, мы должны двигаться в направлении отрицательных градиентов, т.е. 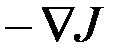 .
.
 2015-08-21
2015-08-21 475
475








