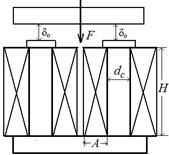
Electromagnets with external forward armature travel

The most widespread forms of electromagnets of this type are electromagnets, presented on fig 1.3. As it follows from pictures, in examined cases there are two identical basic air-gap, in this connection a full electromagnetic force F is determined by a formula

F = 2 F ₀ = 2∙5,1 ∙B ₀²∙ S ₀ / μ₀,

Fig. 1.3, a where В ₀ − induction in a basic air-gap, Wb / сm ²; S ₀ − equivalence cross-section ofeach of basic gaps, сm ².

So, MMF, being on both gaps, determined so:

(w∙I)₀= φ (w∙I)_П = 2∙δ₀∙ B ₀ / μ₀,

where φ − coefficient, taking into account of MMF drop in steel and non-working gaps.

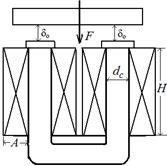Induction В ₀ with a glance of possible in exploitation lowering of MMF (w∙I)_п = χ∙ w∙I, where χ ≤ 1, equals to: B ₀ = μ₀∙φ∙χ∙ w∙I / 2δ₀

Permissible MMF w∙I of electromagnet coils is determined coming from its operation mode, terms of heating and presence of two coils, having a cooling surface 2 S_cl.

a) Continuous running duty of Fig. 1.3, b electromagnet

For this mode next correlations, similar to got before, are correct. Resistance of one coil:

R = 10^-4∙ρ∙π∙(1 + n)∙ d_c∙w / 2 S_m

where w − total number of loops of both coils; S_m – cross-section of wire metal, equals to:

S_m= 2 f_ap∙m∙n∙ d_c ² / w.

So, general losses in resistance of electromagnet are equal to:

P = 2 R∙I ² = 10^-4∙ρ∙π ∙ (1 + n)∙ w ² ∙I ² / f_ap∙m∙n∙d_c

On the other hand, Р is determined from correlation

Θ_per= P / 2 h∙S_cl = P / [2 h∙ (S_ex + α∙ S_in)].

Substituted Р and S_cl from (1.5) into the formula Θ _per, we will define the value of MMF of electromagnet:

w∙I = 2√[10⁴∙ f_ap∙m ² ∙n∙ (1 + 2 n + α)∙ h∙ Θ_per∙ d_c ³ / ρ(1 + n)]

the value of electromagnetic force

F = 8∙10⁴∙μ₀∙φ²∙ε²∙χ²∙ f_ap ∙τ²∙ m ²∙ n ∙(1+ 2 n + α)∙ h∙ Θ_per∙ d_c ⁵/ [ρ(1 + n) δ₀²],

and key size of a core

d_с = ⁵√{[10³∙ρ∙(1 + n)∙ F∙ δ₀² / [φ²∙ε²∙χ²∙ f_ap ∙τ²∙ m ²∙ n ∙(1+ 2 n + α)∙ h∙ Θ_per]}

Designating, as well as before,

C ₁ = [2∙10³∙ρ(1+ n)] / [φ²∙χ² ∙f_ap∙ τ² ∙m ² ∙n∙ (1+2 n +α)∙ h∙ Θ _per ], we will get accordingly:

F = 2ε²∙ d_c ⁵ / (C ₁∙ δ₀²) (1.42)

and d_c = ⁵ √ [ C ₁∙ F ∙δ₀² / 2ε²] (1.43)

Transformation of the last formula gives dependence

F / δ₀³ = 2ε²∙χ⁵ / C ₁, (1.44)

facilitating, as it was explained before, determination of d_c = χ∙δ₀. Thus under F they understand full force of electromagnet. In this case we determine:

1) MMF of coils

w∙I = (9∙10³∙ d_c / φ∙χ∙τ)∙√(d_c/ C ₁) (1.45)

2) cross-section of wire

S_m = [2.82∙ρ∙(1 + n)∙ d_c ² / (φ∙χ∙τ∙ U)]∙√(d_c / C ₁) (1.46)

3) number of coil loops

w = U∙√ [10³∙ f_ap∙n / ρ∙(1 + n)∙(1 + 2 n + α)∙ h∙ Θ _per ∙ d_c)] = C ² ∙U∙√ (C ₁ /d_c) (1.47)

4) induction in a working air-gap

B ₀= (0,396∙10^-4√ F) / (τ∙ε∙ d_c)

approximately by a formula

B ₀ ≈ (4∙10^-5 / τ∙ ⁵√ C ₁)∙√(F ³/ δ₀⁴)

b) Recursive short-time mode

Conclusions, similar to given above, determine next correlations for the electromagnets of this type:

F = 2 p ² _cr∙ε ² ∙d ⁵ _c / (C ₁ ∙ δ₀²) (1.48) d_c = ⁵ √ [ C ₁ ∙F∙ δ₀² / (2 p ² _cr∙ε ²)] (1.49)

F / δ₀³= 2 p ² _cr∙ε ²χ⁵ / C ₁(1.50)

w∙I = (9∙10³∙ p_cr ∙ d_c / φ∙χ∙τ)∙√(d_c / C ₁) (1.51)

S_m = [2.82∙ρ∙(1 + n)∙ p_cr ∙ d_c ² / (φ∙χ∙τ∙ U)]∙√(d_c / C ₁) (1.52)

w = (U/ p_cr) ∙√ {10³∙ f_ap∙n / [ρ∙(1 + n)∙(1 + 2 n + α)∙ h∙ Θ _per ∙ d_c)]}(1.53)

The coefficient of overcurrent p_cr can be defined under the set size of relative duty ratio DR _%: p_cr = √100 / DR _%.

c) Short-time duty

In this mode, ignoring heat emission from a surface, they accept, that all radiated heat in a coil goes to heating of active material. For electromagnets with externalforward armature travel and two coils it is got a like § 1.1:

permissible current density in the cross-section of wire

j = I / S_m = w∙I / (2 f_ap∙m∙n∙d ² _c),

MMF of electromagnet

w∙I = 2 f_ap∙m∙n∙j∙d ² _c,

induction in a basic air-gap

B ₀ = μ₀ ∙ φ∙χ ∙ w∙I / 2δ₀,

full electromagnetic force

F = 5,1π∙μ₀ ∙ φ²∙χ² ∙j ² ∙f ² _ap∙m ² ∙n ² ∙ε ² ∙τ ² ∙d ⁶ _c / δ₀².