Провести возможные упрощения платежной матрицы в следующих задачах:
1)
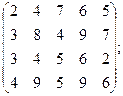
| 2)
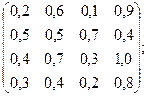
|
3)
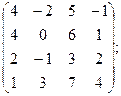
| 4)
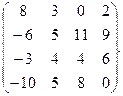
|
1.2.2. Элементарные приемы решения игр 2´2
Пусть дана матричная (2´2)-игра 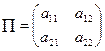 . Может оказаться, что эта игра имеет седловую точку, если это так, то никакой проблемы нет. Предположим, что игра не имеет седловой точки. Отсюда следует, что оптимальные стратегии
. Может оказаться, что эта игра имеет седловую точку, если это так, то никакой проблемы нет. Предположим, что игра не имеет седловой точки. Отсюда следует, что оптимальные стратегии 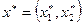 и
и 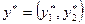 должны иметь положительные компоненты. Далее, если цена игры есть
должны иметь положительные компоненты. Далее, если цена игры есть 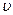 , то
, то
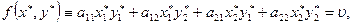 или
или
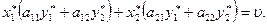 (1.10)
(1.10)
Так как 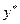 , по предположению, является оптимальной стратегией, то каждое из двух выражений в скобках в левой части (1.10) меньше или равно
, по предположению, является оптимальной стратегией, то каждое из двух выражений в скобках в левой части (1.10) меньше или равно 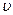 (почему?). допустим, что одно из этих выражений меньше
(почему?). допустим, что одно из этих выражений меньше 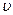 , т.е. допустим, что
, т.е. допустим, что
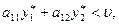 (1.11)
(1.11)
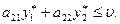 (1.12)
(1.12)
Тогда, поскольку 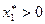 и
и 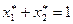 , левая часть в (1.10) будет строго меньше
, левая часть в (1.10) будет строго меньше 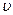 . Отсюда следует, что оба выражения, заключенные в скобки в (1.10), должны быть равны
. Отсюда следует, что оба выражения, заключенные в скобки в (1.10), должны быть равны 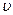 . Значит,
. Значит,
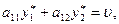 (1.13)
(1.13)
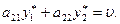 (1.14)
(1.14)
Аналогично можно показать, что
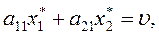 zx (1.15)
zx (1.15)
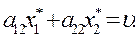 (1.16)
(1.16)
Тем самым мы установили в частном случае справедливость следующей важной теоремы.
Теорема. Если один из игроков применяет свою оптимальную смешанную стратегию, то его выигрыш равен цене игры 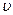 вне зависимости от того, с какими вероятностями будет применять второй игрок стратегии, вошедшие в оптимальную (в том числе и чистые стратегии).
вне зависимости от того, с какими вероятностями будет применять второй игрок стратегии, вошедшие в оптимальную (в том числе и чистые стратегии).
|
|
|
Теперь присоединив к уравнениям (1.15), (1.16) соотношение
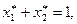 (1.17)
(1.17)
можем решить эту систему трех уравнений с тремя неизвестными 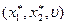 и найти оптимальные вероятности
и найти оптимальные вероятности 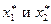 и цену игры
и цену игры 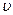 по формулам
по формулам
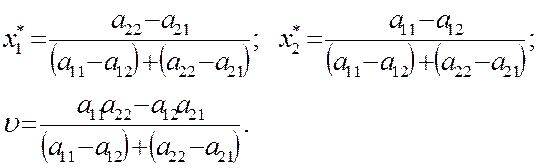 (1.18)
(1.18)
Аналогично, составив систему из уравнений (1.13), (1.14)
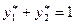 (1.19)
(1.19)
находим оптимальную смешанную стратегию для игрока В.
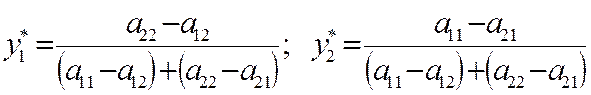
Для геометрического анализа проведенных рассуждений воспользуемся следующим построением. В системе координат xOy отложим на оси Ox отрезок 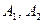 единичной длины, каждой точке х которого будет отвечать некоторая смешанная стратегия
единичной длины, каждой точке х которого будет отвечать некоторая смешанная стратегия 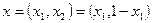 (рис. 1).
(рис. 1).
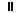
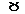
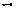
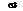
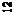
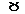
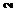
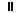
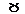
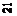
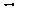
Так точке 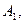 для которой
для которой 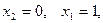 отвечает стратегия
отвечает стратегия 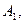 точке
точке 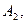 для которой
для которой 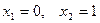 - стратегия
- стратегия 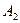 и так далее. По оси ординат будем откладывать выигрыши игрока А. При использовании стратегии
и так далее. По оси ординат будем откладывать выигрыши игрока А. При использовании стратегии 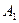 выигрыш равен
выигрыш равен 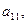 если второй игрок применяет
если второй игрок применяет 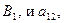 если второй игрок применяет
если второй игрок применяет 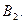 Следовательно, получим две точки
Следовательно, получим две точки 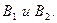 Соответственно, при использовании стратегии
Соответственно, при использовании стратегии 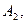 выигрыши могут быть
выигрыши могут быть 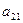 (при
(при 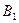 ) или
) или 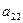 (при
(при 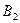 ); они показаны двумя точками
); они показаны двумя точками 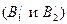 на перпендикуляре, восстановленном в точке
на перпендикуляре, восстановленном в точке 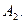 Средний выигрыш
Средний выигрыш 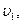 при любом сочетании стратегий
при любом сочетании стратегий 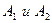 (с вероятностями
(с вероятностями 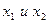 ) и стратегии
) и стратегии 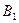 второго игрока равен
второго игрока равен 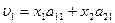 и геометрически определяется ординатой, восстановленной в точке х до пересечения с отрезком
и геометрически определяется ординатой, восстановленной в точке х до пересечения с отрезком 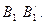 Аналогично, средний выигрыш при использовании стратегии
Аналогично, средний выигрыш при использовании стратегии 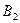 будет определяться ординатами точек, лежащих на отрезке
будет определяться ординатами точек, лежащих на отрезке 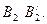
Ординаты точек, лежащих на ломаной 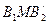 (показанной жирной линией), характеризуют минимальный выигрыш игрока А при использовании им любой смешанной стратегии х (на участке
(показанной жирной линией), характеризуют минимальный выигрыш игрока А при использовании им любой смешанной стратегии х (на участке 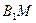 против стратегии
против стратегии 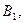 а на участке
а на участке 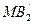 - против стратегии
- против стратегии 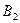 ).
).
|
|
|
Следуя принципу максимина, получаем, что оптимальное решение игры определяет точка М, в которой этот минимальный выигрыш достигает максимума. Ей отвечает на оси абсцисс оптимальная стратегия 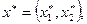 а ее ордината равна цене игры
а ее ордината равна цене игры 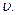 По цене игры сразу находится оптимальная стратегия игрока В из уравнений (1.13) и (1.19).
По цене игры сразу находится оптимальная стратегия игрока В из уравнений (1.13) и (1.19).
На рисунке 1 можно показать нижнюю и верхнюю цены игры 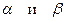 .
.
Если матрица игры имеет седловую точку, то получим следующие разновидности графического изображения игры.
1) Решением игры для игрока А является чистая стратегия 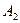 (для игрока В – стратегия
(для игрока В – стратегия 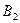 ), т.е.
), т.е.  . Игра имеет седловую точку
. Игра имеет седловую точку 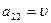 , равную цене игры (рис. 2).
, равную цене игры (рис. 2).
2) Решение игры соответствует точке 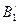 и задается векторами
и задается векторами 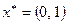 и
и 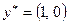 . Игра имеет седловую точку
. Игра имеет седловую точку 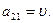 Стратегия
Стратегия 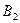 доминируемая и явно невыгодна для игрока В (рис. 3).
доминируемая и явно невыгодна для игрока В (рис. 3).

 2015-08-21
2015-08-21 320
320








