Розрахунок показників надійності за результатами експлуатаційних випробувань

І. Мета та завдання роботи

Мета роботи - опанувати методику аналітичного визначення основних теоретичних законів розподілу випадкових величин та показників безвідмовності невідновлюваних технічних об’єктів.

Завдання роботи:

1. За даними емпіричного статистичного ряду показника надійності (видається індивідуально студентові) визначити основні статистичні характеристики (дослідну ймовірність, оцінку математичного сподівання та середньоквадратичного відхилення, коефіцієнт варіації).

2. Побудувати гістограму, полігон розподілу показника надійності і висунути гіпотезу про закон розподілу.

3. Визначити теоретичну частоту і побудувати теоретичну криву розподілу.

4. Перевірити відповідність (близькість) емпіричного і теоретичного розподілу за критерієм згоди А.М. Колмогорова.

5. Визначити ймовірність безвідмовної роботи технічного об’єкта у заданому інтервалі часу чи в межах заданого напрацювання.

6. Визначити середнє напрацювання об’єкта до відмови та інтенсивність відмов.

7. За допомогою графоаналітичного методу визначити гамма-відсоткове напрацювання до відмови.

ІІ. Теоретичні відомості

Показники надійності машин – напрацювання до відмови, строк служби, час відновлення і т.ін. – за своєю природою є випадковими величинами у статистично-ймовірнісному розумінні. У теорії ймовірностей – математичній науці, що вивчає закономірності у випадкових явищах, важливими характеристиками випадкової величини є математичне сподівання і середньоквадратичне відхилення. Однак ці характеристики є точковими і не відображають тенденції зміни випадкових величин. Найбільш універсальною і вичерпною характеристикою випадкової величини є закон розподілу, який виражає у математичній формі функцію розподілу ймовірностей F(x) або функцію щільності розподілу ймовірностей f(x). Якщо відомий закон розподілу відмов, то легко визначити будь-яку характеристику надійності. Знання закону розподілу відмов дозволяє оцінити надійність машин, вузлів, деталей, розробити заходи підвищення їх надійності при конструюванні,

виготовленні та експлуатації, а також вирішувати практичні задачі у плануванні технічного обслуговування та ремонту. Отже, дані про закони розподілів показників надійності потрібні і використовуються при конструюванні, виготовленні, експлуатації та ремонті машин, вузлів, деталей (див. табл. 1 та рис. 1, 2, 3).

Роботоздатний технічний об’єкт – це об’єкт, ремонт якого неможливий або не передбачений нормативно – технічною документацією.

Ймовірність безвідмовної роботи – це ймовір­ність того, що при певних умовах експлуатації в заданому інтервалі часу чи в межах заданого напрацювання відмови об’єкта не відбудеться, причому

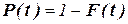, (6)

де F(t) – функція ймовірності відмов.

Ймовірність того, що відмова наступить в інтервалі часу чи напрацювання від t₁ дo t₂ визначиться за формулою

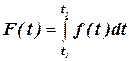, (7)

де f(t) – функція щільності розподілу напрацювань до відмови, яка встановлюється на основі обробки статистичних даних про відмови технічного об’єкта.

Середнє напрацювання до відмови t_c – це математичне сподівання напрацювання об’єкта до першої відмови, причому

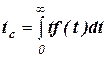. (8)

Інтенсивність відмов – це ймовірність відмови технічного об’єкта за одиницю часу після моменту часу t, за умови, що до моменту часу t відмови не було, причому

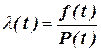. (9)

Гама-відсоткове напрацювання до відмови – це напрацювання, протягом якого відмова об’єкта не виникає з ймовірністю γ, вираженою у відсотках.

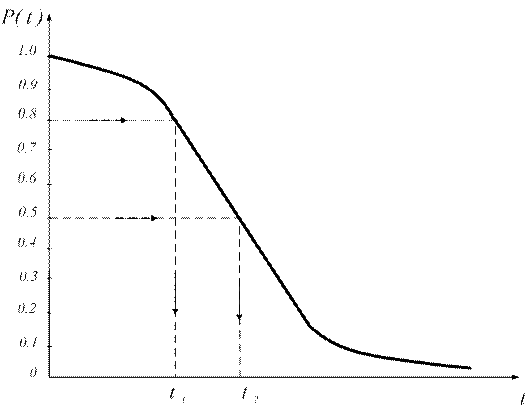
Рис. 4. Графоаналітичний метод визначення гамма-відсоткового напрацювання до відмови

Гама-відсоткове напрацювання до відмови визначають графічно (рис. 4). За заданим значенням функції ймовірності безвідмовної роботи P(t) визначають гама-відсоткове напрацювання. Наприклад, при γ = 80% відповідне напрацювання називається „вісімдесятивідсотковим”. Вісімдесятивідсоткове напрацювання відповідає t_{1 ,} а п’ятдесятивідсоткове t_{2 .}

ІІІ. Методика виконання роботи

1. Складають таблицю інтервального статистичного (варіаційного) ряду (табл. 12), який має чотири параметри: перший – границі кожного інтервала; другий – частоту m_i в кожному інтервалі; третій - дослідну ймовірність в кожному інтервалі P_i; четвертий – накопичену (інтегральну) дослідну ймовірність .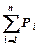

Кількість інтервалів n залежить від величини вибірки, крім того

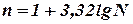, (10)

де N - величина вибірки (кількість статистичних даних).

Кількість рядків у таблиці 12 відповідає числовому значенню параметра n. Практично беруть n у межах від 7...20 та визначають крок інтервалу за формулою:

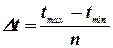, (11)

де t_max, t_min – відповідно максимальне та мінімальне значення досліджуваної величини.

Якщо величина інтервалу одержується дробовою, то її доцільно заокруглити до цілих чисел або зручних для розрахунків дробів. При цьому мінімальна кількість значень досліджуваної величини, що попадає в інтервал, повинна бути в межах 3...5. Всі інтервали повинні бути однакові, прилягати один до одного та не мати розривів.

Таблиця 12.

Інтервальний статистичний ряд

Границі інтервалів	mi	Pi = m i / N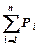
…………	…………	…………	…………

2. Визначають статистичну оцінку математичного сподівання 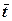та середньоквадратичного відхилення S,а також коефіцієнт варіації ν за відповідними формулами:

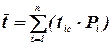, (12)

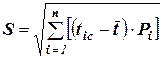, (13)

де 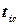– значення середини і -того інтервалу.

3. Виконують перевірку на випадаючі точки по правилу 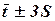. Якщо t_min не виходить за межу 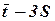, а t_max не виходить за межу 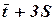, то перевірка виконується. Якщо перевірка не виконується, то випадаючі точки необхідно вилучити зі статистичного ряду та побудувати новий інтервальний статистичний ряд, перерахувати оцінку математичного сподівання 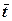, середньоквадратичне відхилення S та коефіцієнт варіації ν.

4. На основі отриманих параметрів емпіричного розподілу будують гістограму, полігон та криву накопичених дослідних ймовірностей, які дають змогу висунути гіпотезу про закон розподілу випадкової величини.

По осі абсцис відкладають інтервали показника надійності, а по осі ординат дослідну ймовірність 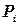(для гістограми та полігону) та накопичену дослідну ймовірність 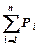(для графіка накопичених дослідних ймовірностей). Ординати гістограми та полігону повинні відповідати серединам кожного інтервалу, а ординати накопиченої дослідної ймовірності – кінцям кожного інтервалу. Гістограма, полігон, крива накопичених дослідних ймовірностей зображені на рис 5.

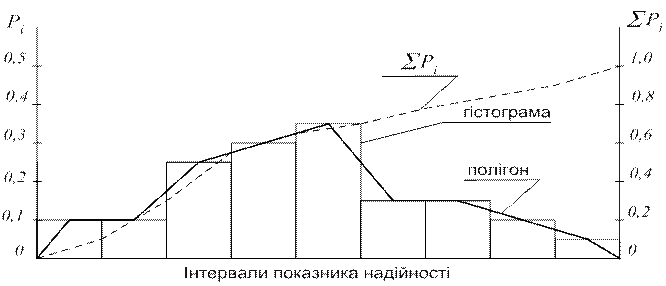
Рис. 5. Гістограма, полігон, крива накопичених дослідних ймовірностей

Додатковими даними для висунення гіпотези може служити величина коефіцієнта варіації. Якщо коефіцієнт варіації (див. формулу (2)) знаходиться в межах 0,08...0,33, то висувається гіпотеза про нормальний закон розподілу; 0,33...0,63 - про закон Вейбулла; 0,63...1,30 - про експоненціальний закон.

5. Визначають параметри функції ймовірностей інтервалів 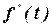(ідентична по формі до диференціальної функції даного закону розподілу випадкової величини), причому

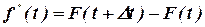, (14)

де 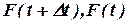- значення інтегральних функцій даного закону розподілу випадкової величини відповідно в кінці та на початку кожного інтервалу.

У випадку висування гіпотези щодо закону нормального розподілу використовують оцінку математичного сподівання 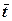та середньоквадратичного відхилення S (див. табл. 1). Значення інтегральної функції визначають із табл. 13 за центрованими значеннями аргументів, які визначають для кожного інтервалу за формулою

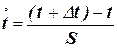, (15)

де 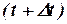- кінцеве значення інтервалу, t – початкове значення інтервалу.

Якщо 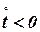, то необхідно виконати перерахунок інтегральної функції, а саме

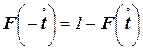. (16)

Таблиця 13.

Значення центрованої інтегральної функції

закону нормального розподілу (Гаусса)

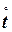
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,8 3,0	0,5 0,54 0,579 0,618 0,655 0,691 0,726 0,758 0,788 0,816 0,841 0,864 0,885 0,903 0,919 0,933 0,945 0,955 0,964 0,971 0,977 0,982 0,986 0,989 0,992 0,994 0,995 0,997 0,999	0,504 0,544 0,583 0,622 0,659 0,695 0,729 0,761 0,791 0,819 0,844 0,867 0,887 0,905 0,921 0,934 0,946 0,956 0,965 0,972 0,978 0,983 0,986 0,990 0,992 0,994 0,995 0,998 0,999	0,508 0,548 0,587 0,626 0,663 0,699 0,732 0,764 0,794 0,821 0,846 0,869 0,889 0,907 0,922 0,936 0,947 0,957 0,966 0,973 0,978 0,983 0,987 0,990 0,993 0,994 0,996 0,998 0,999	0,512 0,552 0,591 0,629 0,666 0,702 0,736 0,767 0,797 0,824 0,849 0,871 0,891 0,908 0,924 0,937 0,948 0,958 0,966 0,973 0,979 0,983 0,987 0,990 0,992 0,994 0,996 0,998 0,999	0,516 0,556 0,595 0,633 0,670 0,705 0,739 0,770 0,800 0,826 0,851 0,873 0,893 0,910 0,925 0,938 0,950 0,959 0,967 0,974 0,979 0,984 0,987 0,990 0,992 0,994 0,995 0,998 0,999	0,520 0,560 0,599 0,637 0,674 0,709 0,742 0,773 0,802 0,829 0,853 0,875 0,894 0,911 0,926 0,939 0,951 0,960 0,968 0,974 0,980 0,984 0,988 0,991 0,993 0,995 0,996 0,998 0,999	0,524 0,564 0,603 0,641 0,677 0,712 0,745 0,776 0,805 0,831 0,855 0,877 0,896 0,913 0,928 0,941 0,952 0,961 0,969 0,975 0,980 0,985 0,988 0,991 0,993 0,995 0,996 0,998 0,999	0,528 0,568 0,606 0,644 0,681 0,716 0,749 0,779 0,808 0,834 0,858 0,879 0,898 0,915 0,929 0,942 0,953 0,962 0,969 0,976 0,981 0,985 0,988 0,991 0,993 0,995 0,996 0,998 0,999	0,532 0,571 0,610 0,648 0,684 0,719 0,752 0,782 0,811 0,837 0,860 0,881 0,900 0,916 0,931 0,943 0,954 0,962 0,970 0,976 0,981 0,985 0,989 0,991 0,993 0,995 0,996 0,998 0,999	0,536 0,575 0,614 0,652 0,688 0,722 0,755 0,785 0,813 0,839 0,862 0,883 0,902 0,918 0,932 0,944 0,955 0,963 0,971 0,977 0,982 0,986 0,989 0,992 0,994 0,995 0,996 0,998 0,999

У випадку висування гіпотези щодо закону розподілу Вейбулла використовують: а - параметр масштабу, b - параметр форми, с - параметр зміщення (див. табл. 1), які визначають за наближеними формулами:

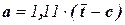, (17)

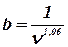, (18)

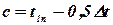, (19)

де 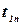- значення початку першого інтервалу.

У випадку висування гіпотези щодо експоненціального закону розподілу використовують параметр λ - інтенсивність відмов (див. табл. 1), причому

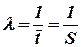. (20)

Визначивши числові значення інтегральних функцій та функції ймовірностей інтервалів для певного закону розподілу випадкової величини, далі наносять відповідні ординати на графік (ординати інтегральних функцій по кінцях кожного інтервалу, а ординати функції ймовірностей інтервалів по середині кожного інтервалу), апроксимуючи (згладжуючи) дослідну криву полігон та криву накопичених дослідних ймовірностей (рис. 6).

Рис. 6. Графічна обробка статистичних даних

6. Перевіряють правильність передбачуваного закону розподілу показника надійності, тобто близькість емпіричного і теоретичного розподілу, за критерієм згоди А.М. Колмогорова.

Таблиця 14.

Перевірка правильності вибору передбачуваного закону розподілу

показника надійності

				-
......	......	......	......	......
......	......	......	......	......

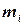
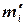
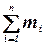
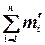
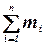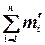
Кількість рядків у таблиці 14 відповідає n, а теоретична частота 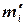визначається за формулою

. (21)

Далі визначають значення аргументу L функції ймовірності передбачуваного закону розподілу P(L), причому

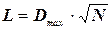, (22)

де

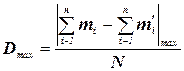. (23)

Значення функції P(L) наведені у таблиці 15. Якщо P(L)≥ 0,05, то одержане розходження викликане випадковими величинами і не заперечує прийняття даного теоретичного закону. Якщо P(L)< 0,05, то ймовірність згоди вважається незадовільною та необхідно вибрати інший теоретичний закон.

Таблиця 15.

Числові значення функції ймовірності P(L)

L	P(L)	L	P(L)	L	P(L)
0,30 0,35 0,40 0,45 0,50 0,55 0,58 0,60 0,64 0,65 0,70	0,9997 0,9972 0,9874 0,9639 0,9228 0,8896 0,8643 0,8073 0,7920 0,7112	0,75 0,80 0,85 0,90 0,95 1,00 1,10 1,20 1,30 1,40 1,50	0,6272 0,5441 0,4653 0,3927 0,3275 0,27 0,1777 0,1122 0,0681 0,0597 0,0222	1,60 1,70 1,80 1,90 2,00 2,10 2,20 2,30 2,40 2,50 -	0,012 0,0062 0,0032 0,0015 0,0007 0,0003 0,0001 0,0001 0,0000 0,0000 -

7. Визначити ймовірність безвідмовної роботи технічного об’єкта у заданому інтервалі часу чи в межах заданого напрацювання за формулою (7).

8. Визначити середнє напрацювання об’єкта до відмови та інтенсивність відмов за формулами (8, 9).

9. За допомогою графоаналітичного методу визначити гама-відсоткове напрацювання до відмови (див. рис. 4).

IV. Звіт

У звіті про роботу необхідно вказати назву роботи, послідовність виконання, провести необхідні розрахунки, заповнити таблиці, побудувати гістограму, полігон, криву накопичених дослідних ймовірностей, теоретичну криву розподілу та інтегральну функцію, зробити висновки про правильність вибору передбачуваного закону розподілу випадкових величин та щодо визначених показників надійності невідновлюваних технічних об’єктів.

Лабораторна робота № 3 (4 год.)