Тета-логистическая модель (Theta-Logistic Predator-Prey)

В отличие от модели Лотки-Вольтерры, данная модель более реалистич­на и в меньшей степени упрощает исследуемый процесс, включая в него не только зависимый от плотности рост популяции жертвы, но и нелиней­ные функциональные ответы хищника. Поэтому очень полезно сравнить результаты, даваемые обеими этими моделями при сходных начальных условиях.

В тета-логистической модели для описания роста популяции жертвы в отсутствие хищников использована очень известная модификация логистического уравнения, в которой есть дополнительный параметр (показатель степени), обозначаемый греческой буквой тета (θ) и позволяю­щий отражать различные типы зависимости скорости роста от плотности:

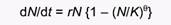(7)

Эта модель зависимого от плотности популяционного роста была впервые предложена Ayala and Gilpin в 1973 г. Легко заметить, что в том случае, когда тета равна единице, уравнение 7 превращается в классичес­кое логистическое уравнение dN/dt = r N {(К-N /)/ K }. Если значение тета больше единицы и достаточно велико, рождаемость и смертность существенно не изменяются до тех пор, пока численность популяции не приблизится к предельной емкости среды обитания. В этом случае для популяции характерен бурный экспоненциальный рост, завершающийся быстрым торможением и почти внезапным выходом на плато. Если же величина тета заметно меньше единицы, то удельная рождаемость очень быстро уменьшается, а смертность увеличивается вследствие роста численности уже при небольших плотностях популяции. Поэтому для популяции характерен замедленный рост с постепенным приближением к предельной емкости среды.

Для того, чтобы отразить влияние хищника на рост популяции жертвы, в уравнение 7 следует ввести скорость изъятия особей жертвы F (см. уравнение 3) со знаком "минус":

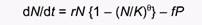(8)

В этом уравнении Р - это численность популяции хищника, а f -функцио­нальный ответ хищника, вычисляемый по дополнительным уравнениям (см. ниже).

Динамика популяции хищника в тета-логистической модели представле­на уравнением:

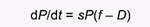(9)

Здесь s - это коэффициент эффективности переработки поглощенной хищником пищи в его потомство, f- функциональный ответ хищника, a D - это та минимальная удельная скорость потребления жертв, при которой популяция хищника не растет, но и не вымирает, т.е. рождаемость в ней точно компенсирует смертность (каждая особь хищника оставляет только одного потомка). Это уравнение роста популяции в неявной форме содержит два предположения: (1) плотность популяции хищника прямо не влияет на шансы составляющих ее особей погибнуть или оставить потомство; это влияние может быть только опосредованным через воздействие на популяцию жертвы, и (2) число выживших потомков одной особи хищника прямо пропорционально количеству потребленных им жертв.

Строго говоря, уравнение 9 фактически идентично уравнению 6 модели Лотки-Вольтерры. Действительно, мы можем преобразовать его в уравнение 6 следующим образом:

dP/dtf = sPf- sPD = sC₁NP - sDP = C₂NP - r₂P,

поскольку f= C₁N, sC₁ = C₂, а произведение sD можно обозначить как r₂ (действительно, если умножить минимальную удельную скорость потребления D на коэффициент эффективности s, то мы получим ту величину минимальной удельной рождаемости, которая компенсирует смертность хищника r₂ при отсутствии пищи).

Еще одним компонентом тета-логистической модели является функциональный ответ хищника, обозначенный в уравнениях 8 и 9 буквой f. Этот параметр может быть определен экспериментально в лаборатор­ных или полевых условиях. Канадский эколог С. S. Holling (1965) выделил три основных типа функциональных ответов, описание и примеры которых можно найти в большинстве учебников по экологии.

Функциональный ответ типа 1 (f₁) был определен выше уравнением 2, в котором удельная скорость потребления жертвы хищником линейно возрастает с увеличением плотности ее популяции. Конечно, в реальных условиях скорость поедания жертв не может возрастать бесконечно и достигает некоторой предельной величины в тот момент, когда хищник уже просто физически неспособен поедать больше жертв в единицу времени. Однако в рассматриваемой модели для упрощения предполагает­ся, что подобного насыщения не происходит и f₁, линейно зависит от плотности популяции при любых значениях последней.

Функциональный ответ типа 2 возникает в тех случаях, когда хищник затрачивает некоторое время на обработку каждой пойманной добычи и в эти моменты уже не может заниматься поисками новых жертв. В такой ситуации, чем чаще хищник ловит жертв, тем меньше времени у него остается для продолжения охоты. Поэтому уравнение 1, определяющее число жертв, встреченных и съеденных одним хищником N_с, должно быть переписано следующим образом:

(10)

где T_s - время, затраченное непосредственно на поиски новых жертв. Если T_н - это среднее время, необходимое для поимки и поедания одной жертвы, а T- общее время наблюдений, то:

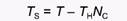(11)

Подставляя это выражение в уравнение 10, мы получаем:

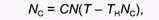
или, после преобразований:

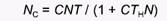(12)

Это уравнение описывает функциональный ответ типа 2 и известно под названием "дисковое уравнение Холлинга", потому что Холлинг впервые получил ответ типа 2, проведя эксперимент, в котором ассистент с завязанными глазами должен был на ощупь собирать со стола ("охотить­ся на") разбросанные в случайном порядке кружочки (диски) наждачной бумаги. Из уравнения 12 легко получить зависимость удельной скорости потребления жертв от их плотности, т.е. собственно функциональный ответ типа 2:

(13)

Для данной зависимости характерен постепенно замедляющийся рост удельной скорости потребления жертв при увеличении их плотности с асимптотическим приближением к величине f₂ = 1/T_н при N à ∞, когда практически все время хищник затрачивает на обработку жертв.

И, наконец, ответ типа 3 описывают сигмоидные, или S-образные кривые. Это означает, что при низких плотностях жертвы скорость ее потребления хищником невелика, затем очень быстро увеличивается (вследствие так называемого переключения, а также изменений, связан­ных с обучением хищника и формированием у него предпочтения к данному виду пищи) и только после этого начинает уменьшаться, постепенно выходя на плато. Существует множество математических формул, пригодных для описания ответа 3 типа, но чаще всего использу­ют следующее выражение, являющееся модификацией уравнения 13:

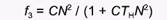(14)

Для данной зависимости характерен сигмоидный рост удельной скорости потребления жертв при увеличении их плотности. При очень высокой плотности жертвы кривая асимптотически приближается к той же величине 1/T_н, что и в случае ответа типа 2.

Таким образом, в тета-логистической модели предусмотрено использова­ние одного из трех типов функционального ответа f- параметра, входяще­го в оба основных уравнения модели 8 и 9. Для вычисления f применяют, соответственно, уравнения 2, 13 и 14.

Розенцвейг и Макартур (Rosenzweig and MacArthur, 1963) разработали новый метод, широко известный теперь как фазово-плоскостной анализ и позволяющий определить, будет ли система хищник-жертва испытывать циклические колебания, или нет. Этот метод в деталях описан в больши­нстве учебников по экологии. Фазовая (или фазово-плоскостная) диаграм­ма системы хищник-жертва - это график, по оси абсцисс которого отложена плотность популяции жертвы, а по оси ординат - плотность популяции хищника. Метод предполагает проведение двух линий, именуемых изоклинами. Первая из них - изоклина хищника - это вертикальная линия, представляющая плотность жертвы, при которой скорость роста популяции хищника равна нулю. Вторая – изоклина жертвы - это линия, соответствующая таким значениям плотностей популяций жертвы и хищника, при которых нулю равна скорость роста популяции жертвы. Розенцвейг и Макартур установили, что если изоклина жертвы имеет положительный наклон (возрастающие значения Р ) втом месте, где обе изоклины пересекаются, то популяции хищника и жертвы будут испытывать незатухающие циклические сопряженные колебания, если же наклон изоклины жертвы отрицателен (уменьшающиеся значения Р ), то колебания численности не возникнут, или же будут затухающими, и популяции хищника и жертвы обязательно достигнут состояния равновесия при постоянной численности.

Тета-логистическая модель дает нам прекрасные возможности проверить предсказания Розенцвейга и Макартура в разных исходных условиях.