Понятие макронаблюдаемой играет фундаментальную роль в статистической механике. Соответственно, установление численных значений макронаблюдаемых и взаимосвязей между ними — центральная задача этой науки. Выше было отмечено, что объективное и точное вычисление средних по времени требует выполнения огромного числа измерений в течение длительного времени. Поэтому необходим иной способ решения задачи нахождения численных значений макронаблюдаемых. Этот способ состоит в использовании особой модели, которая называется статистическим ансамблем.
Рассмотрим последовательность измерений энергии, произведенных над частицей, находящейся в контакте с окружающей средой. Предположим, что полный спектр энергетических состояний частицы исчерпывается 6 уровнями: Е 1, Е 2, …, Е 6. Тогда в серии измерений мы будем получать именно эти 6 чисел, следующих друг за другом в случайном порядке.
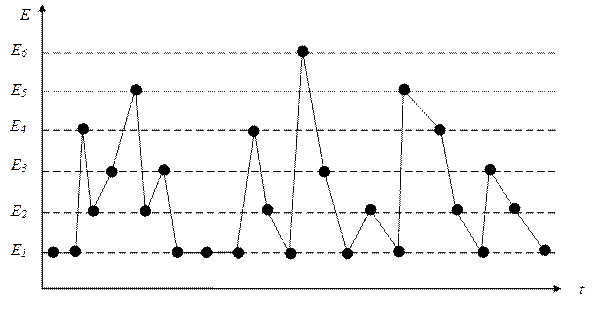
Полученное изображение спроектируем вдоль оси времени на ось энергий. Тогда на каждом энергетическом уровне, доступном частице, сгруппируется определенное число результатов измерений: ni.
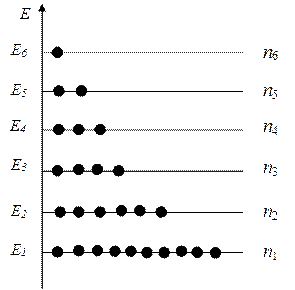
Теперь для каждого допустимого результата измерения энергии можно определить особую характеристику — долю от общего числа результатов измерений:
n i = ni / å ni
Эти числа показывают, что некоторые результаты измерений встречаются в серии чаще, а другие — реже. Следовательно, наша частица проводит в одних состояниях больше времени, а в других — меньше.
Когда длина серии измерений стремится к бесконечности, числа n i стремятся к определенным предельным значениям, которые называются вероятностями:
n i ® Pi (при t ® ¥)
Статистическим ансамблем называется спектр наблюдаемой А с указанными для каждого допустимого значения (Ai) вероятностями (pi):
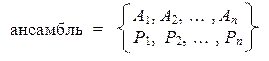
В этом случае спектр наблюдаемой { А 1, А 2, …, Аn } называется спектром ансамбля, а набор вероятностей { P 1, P 2, …, Pn } называется функцией распределения ансамбля.
Конструкция ансамбля предназначена для того, чтобы иметь возможность вычислять значение макронаблюдаемой. Соответствующая формула выглядит так (в математической статистике вычисляемая таким образом величина называется математическим ожиданием случайной величины):
`Aa = P 1 A 1 + P 2 A 2 + … + PnAn = å PiAi
Величина `Aa называется средним по ансамблю и используется как оценка значения макронаблюдаемой `At, т.е. предполагается, что выполняется равенство: `At = `Aa.
Ясно, что для вычисления среднего по ансамблю необходимо знать все вероятности { P 1, P 2, …, Pn }. Их можно определить экспериментально — по результатам достаточно большой серии измерений. Однако главный смысл введения модели ансамбля заключается в том, что эти вероятности можно определить и без измерений — на основании анализа особенностей внутреннего строения статистической системы. В этом случае необходимость выполнения измерений отпадает, и значения макронаблюдаемых можно определить априорно (теоретическим способом).
Рассмотрим для иллюстрации следующий пример. Пусть в качестве системы выступает игральная кость с шестью гранями. У такой системы имеется шесть доступных ей состояний, каждое из которых можно охарактеризовать значением особой наблюдаемой — числом очков на верхней грани. Если кость предоставлена самой себе, она обязательно будет находиться в одном из этих шести состояний, причем выбранное состояние будет точно определенным (не будет изменяться во времени). Теперь подвергнем кость "действию окружающей среды", поставив на стол механический вибратор. За счет действия вибратора кость иногда сможет переворачиваться на другую грань, т.е. совершать "квантовые скачки" из одного состояния в другое. Теперь состояние кости не является строго определенным, и с течением времени кость будет попадать во все доступные ей состояния. Наблюдая в течение времени за такой костью, мы можем получить длинную серию результатов измерений наблюдаемой. Эта серия будет состоять из случайной последовательности целых чисел в интервале от 1 до 6 (например, 1, 3, 5, 4, 2, 6, 1, 2, 2, 4, 3, 6, 5, 2, 1, …), для которой можно вычислить среднее по времени. Как показывает опыт, `At = 3,5.
Теперь, вместо того, чтобы наблюдать длительное время за флуктуирующим состоянием одной кости, возьмем большое число одинаковых костей и высыплем их сразу на стол. Каждая кость упадет случайным образом и зафиксируется в выбранном состоянии навсегда. Глядя на неподвижные кости, мы сможем легко подсчитать доли костей, находящихся в каждом из шести состояний. Эти доли и будут вероятностями ансамбля.
В действительности можно ограничиться только мысленным выполнением этого эксперимента. Вследствие того, что у правильной кости все шесть сторон одинаковы, мы сразу можем заключить, что все шесть вероятностей будут одинаковы между собой, т.е. Pi = 1/6. Таким образом, получаем статистический ансамбль следующего вида:
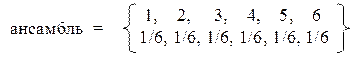
Теперь легко вычислить среднее по ансамблю:
`Aa = å PiAi = (1/6) × (1 + 2 + 3 + 4 + 5 + 6) = 3,5
которое оказывается в точности равным среднему по времени.
Таким образом, смысл модели статистического ансамбля заключается в том, чтобы вместо экспериментального наблюдения за флуктуирующей системой, определять набор вероятностей априорным способом — на основании сведений о ее строении. Если наши сведения о строении системы правильны, выполнение равенства `At = `Aa гарантировано, и, следовательно, мы получаем верную оценку значения интересующей нас макронаблюдаемой.
Конечно, здесь возможны и ошибки. Например, если реальная кость фальшивая (одна из граней тяжелее остальных), а мы будем моделировать ее поведение ансамблем из идеальных костей, то полученный результат будет неудовлетворительным. Тем не менее, для любой статистической системы всегда можно найти адекватную ей модель статистического ансамбля. Более того, несмотря на бесконечное разнообразие систем, для их статистического описания оказывается достаточным использование всего трех разновидностей модели статистического ансамбля:
· микроканонический ансамбль (МКА),
· канонический ансамбль (КА),
· большой канонический ансамбль (БКА),
 2015-10-13
2015-10-13 1039
1039
