Предел функции.
Опр.1. Число  называется пределом функции
называется пределом функции 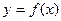 при
при  , если для любой окрестности
, если для любой окрестности  числа
числа  существует такая проколотая окрестность
существует такая проколотая окрестность  числа a, что для всех
числа a, что для всех 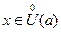 ,
, 
Это определение по Коши. Число  может быть как конечным, так и бесконечным. В частности, если числа
может быть как конечным, так и бесконечным. В частности, если числа  и а конечны, получаем следующее определение (на языке “
и а конечны, получаем следующее определение (на языке “  -
-  ”).
”).
Опр.2. Число  называется пределом функции
называется пределом функции 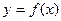 при
при  , если для всякого
, если для всякого 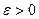 существует такое число
существует такое число  >0, что для всех х, удовлетворяющих неравенству 0<
>0, что для всех х, удовлетворяющих неравенству 0<  <
<  и входящих в область определения функции
и входящих в область определения функции 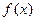 , справедливо неравенство:
, справедливо неравенство:
 (1)
(1)
и обозначается 
Если а = +  , то получаем следующее определение.
, то получаем следующее определение.
Опр.3. Число  называется пределом функции
называется пределом функции 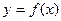 при
при  , если для всякого
, если для всякого 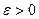 существует такое число
существует такое число  >0, что для всех х, удовлетворяющих неравенству
>0, что для всех х, удовлетворяющих неравенству  и входящих в область определения функции
и входящих в область определения функции 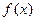 , справедливо (1) и обозначается:
, справедливо (1) и обозначается:
 (определение “
(определение “  -C”).
-C”).
Определение предела функции по Гейне: Число А называется пределом функции y= f (x) при  (в точке a), если для любой сходящейся к числу а последовательности
(в точке a), если для любой сходящейся к числу а последовательности  значений х, входящих в область определения функции и отличных от a, соответствующая последовательность
значений х, входящих в область определения функции и отличных от a, соответствующая последовательность  этой функции сходится к числу А.
этой функции сходится к числу А.
|
|
|
Пример 1. Пользуясь определением предела по Гейне, доказать, что
 .
.
Решение: Рассмотрим любую последовательность  , удовлетворяющую двум условиям:
, удовлетворяющую двум условиям:
1) 

2) 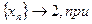
 .
.
Этой последовательности  соответствует последовательность значений функции:
соответствует последовательность значений функции:
 …
…
Тогда на основании свойств сходящихся последовательностей (каких?) будем иметь

Т.о. независимо от выбора последовательности  , сходящейся к числу 2
, сходящейся к числу 2  , соответствующая последовательность значений функции
, соответствующая последовательность значений функции  А это на основании определения предела функции по Гейне значит, что
А это на основании определения предела функции по Гейне значит, что 
Замечание 1: Определением предела по Гейне удобно пользоваться тогда, когда доказывается, что функция f (x) не имеет предела. Для этого достаточно показать, что существует две последовательности  но соответствующие последовательности
но соответствующие последовательности 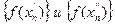 имеют неравные пределы.
имеют неравные пределы.
Пример 2: Доказать, что  не существует.
не существует.
Решение: возьмем

Тогда соответствующие последовательности значений функции таковы:

Следовательно,
 , т.е.
, т.е.  не существует
не существует
Замечание 2: Пример 2 показывает, что вывод о наличии предела функции нельзя делать, исходя из последовательности {xn} частного вида (например, исходя из xn'' =1+  ), а нужно рассматривать произвольную последовательность {xn }, имеющую заданный
), а нужно рассматривать произвольную последовательность {xn }, имеющую заданный
предел а.
Пример 3: Пользуясь "  –
–  " определением предела, доказать, что
" определением предела, доказать, что
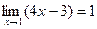

Решение: Надо доказать, что для "e>0 существует такое de >0, что из неравенства 0 < |x-1| < de следует, что | f (x)-1| < e, f (x)=4x-3. Зададим
e > 0 и рассмотрим выражение: | f (x)-1|=|4x-3-1|= 4|x-1|.
|
|
|
Если взять de ≤ e/4, то для всех х, удовлетворяющих неравенству |x-1| < de, будем иметь | f (x)-1| = 4|x-1|<4de ≤ 4e/4=e.
Следовательно, 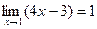
Пример 4: f (x)=1/(x-1) доказать, что 
Решение: По определению  , если для " М>0 можно подобрать dМ>0, что для всех х¹ а, удовлетворяющих неравенству
, если для " М>0 можно подобрать dМ>0, что для всех х¹ а, удовлетворяющих неравенству
0<|x- a |<d, будет выполняться условие  >M. В нашем случае по заданному M>0 будем подбирать dМ из условия
>M. В нашем случае по заданному M>0 будем подбирать dМ из условия
|  1/|x-1|>M Ú |x-1|<1/M.
1/|x-1|>M Ú |x-1|<1/M.
Следовательно, положив dM=1/М, получим, что для всех х, удовлетворяющих неравенству 0<|x-1|<dM, выполняется неравенство  M, значит,
M, значит,

ВАРИАНТЫ.
1. Доказать, что предел функции не существует:







2. Доказать с помощью "e-d" определения существования следующих пределов и по заданным e, подобрать de: e1=0,5;e2=1;e3=1/100.


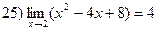
3. Доказать, что



 2015-10-22
2015-10-22 541
541








