Классы точности средств измерений.
Класс точности – это обобщенная метрологическая характеристика, определяющая различные свойства СИ.
Класс точности СИ уже включает систематическую и случайную погрешности. Однако он не является непосредственной характеристикой точности измерений, выполняемых с помощью этих СИ, поскольку точность измерения зависит и от метода измерения, взаимодействия СИ с объектом, условий измерения и т. д.
В частности, чтобы измерить величину с точностью 1%, недостаточно выбрать СИ с погрешностью 1%. Выбранное СИ должно обладать гораздо меньшей погрешностью, т. к. нужно учесть как минимум ещё погрешность метода.
Определяя класс точности, нормируют, прежде всего, пределы допускаемой основной погрешности.
Классы точности присваивают СИ при их разработке по результатам государственных приемочных испытаний.
Пределы допускаемой основной погрешности выражаются в форме абсолютной, относительной или приведенной погрешностей.
Способ выражения погрешностей зависит от характера изменения погрешности по диапазону измерения, назначения и условий применения СИ.
Если погрешность результатов измерений в данной области измерений принято выражать в единицах измеряемой величины или делениях шкалы (меры, магазины номинальных физических величин), то принимается форма абсолютных погрешностей.
Если границы абсолютных погрешностей в пределах диапазона измерений практически постоянны, то принимается форма приведенной погрешности, а если эти границы нельзя считать постоянными, то форма относительной погрешности.
Поэтому ГОСТ 8.401.-80 в качестве основных устанавливает три вида классов точности СИ:
- Для пределов допускаемой абсолютной погрешности в единицах измеряемой величины или делениях шкалы;
- Для пределов допускаемой относительной погрешности в виде ряда чисел:
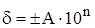 ;
;
где А=1; 1,5; (1,6); 2; 2,5; (3); 4; 5 и 6.
Значения 1,6 и 3 – допускаемые, но не рекомендуемые; n=1; 0; - 1; - 2; …
- Для пределов допускаемой приведенной погрешности с тем же рядом:
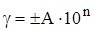 .
.
Наиболее широкое распространение получило нормирование класса точности по приведенной погрешности:
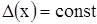 , (аддитивная погрешность)
, (аддитивная погрешность)
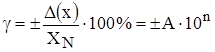 .
.
Где XN – нормирующее значение.
Как правило, в качестве XN берется диапазон измерения СИ или его верхнее значение.
Класс точности обозначается в данном случае, например, следующим образом:
0,5.
Класс точности через относительную погрешность СИ назначается двумя способами:
- Если погрешность СИ имеет в основном только мультипликативную составляющую, то пределы допускаемой основной относительной погрешности устанавливаются по формуле:
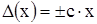 - мультипликативная погрешность;
- мультипликативная погрешность;
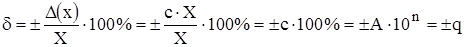 .
.
И обозначается следующим образом:


- Если СИ имеет как мультипликативную, так и аддитивную составляющие, то класс точности обозначается двумя цифрами:
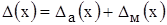 ;
;
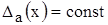 - аддитивная составляющая погрешности;
- аддитивная составляющая погрешности;
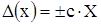 - мультипликативная составляющая погрешности.
- мультипликативная составляющая погрешности.
Тогда относительная погрешность СИ примет следующий вид:
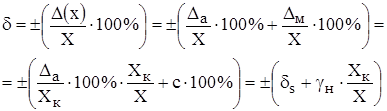 .
.
Или окончательно имеем:
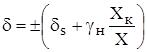 .
.
Здесь:
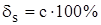 - относительная погрешность, обусловленная мультипликативной составляющей погрешности (погрешность чувствительности);
- относительная погрешность, обусловленная мультипликативной составляющей погрешности (погрешность чувствительности);
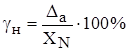 - приведенная погрешность, обусловленная аддитивной составляющей погрешности;
- приведенная погрешность, обусловленная аддитивной составляющей погрешности;
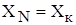 - нормирующее значение, соответствующее верхнему (конечному) значению измеряемой величины.
- нормирующее значение, соответствующее верхнему (конечному) значению измеряемой величины.
При 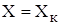 , т. е. когда измеряемая величина принимает значение, равное верхнему значению измеряемого диапазона, имеем:
, т. е. когда измеряемая величина принимает значение, равное верхнему значению измеряемого диапазона, имеем:
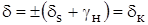 .
.
Здесь 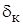 - относительная погрешность для конца диапазона измерения.
- относительная погрешность для конца диапазона измерения.
Класс точности в данном случае представляют следующим образом:
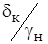 .
.
Например: класс точности 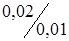 указывает, что погрешность нормирована по двузначной формуле с
указывает, что погрешность нормирована по двузначной формуле с 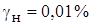 и
и 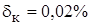 .
.
 Отчет по шкале прибора с пределами измерений 0-50 А и равномерной шкалой составил 25 А. Пренебрегая другими видами погрешностей измерения, оценить пределы допускаемой абсолютной погрешности этого отсчета при использовании различных СИ классов точности: 0,5;;
Отчет по шкале прибора с пределами измерений 0-50 А и равномерной шкалой составил 25 А. Пренебрегая другими видами погрешностей измерения, оценить пределы допускаемой абсолютной погрешности этого отсчета при использовании различных СИ классов точности: 0,5;; 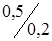 .
.
Решение.
- Для СИ класса точности 0,5.
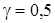 .
.
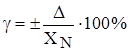 .
.
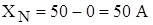 .
.

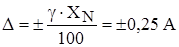 .
.
- Для СИ класса точности
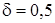 .
.
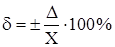 .
.
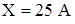 .
.
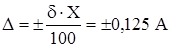 .
.
- Для СИ класса точности
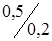 .
.
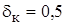 .
.
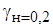 .
.
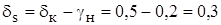 .
.
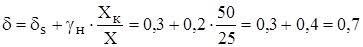 .
.
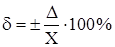 .
.
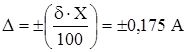 .
.
Лекция № 12.
Любое значение искомого параметра, вычисленное на основе ограниченного числа опытов, всегда будет содержать элемент случайности. Такие приближенное случайное значение будем называть оценкой параметра.
Например, оценкой для математического ожидания может служить среднее арифметическое наблюденных значений случайной величины в n независимых опытах. При очень большом числе опытов среднее арифметическое будет с большей вероятностью весьма близко к математическому ожиданию. Если же число опытов n невелико, то замена математического ожидания средним арифметическим приводит к какой-то ошибке. Эта ошибка в среднем тем больше, чем меньше число опытов. Так же будет обстоять дело и с оценками других неизвестных параметров. Любая из таких оценок случайна. При пользовании ею неизбежны ошибки. Желательно выбрать такую оценку, чтобы эти ошибки были по возможности минимальными.
Оценка математического ожидания: среднее арифметическое с. в. Х
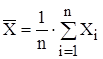 .
.
Оценка дисперсии с. в. Х
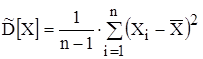 .
.
Оценка с.к.о. с. в. Х
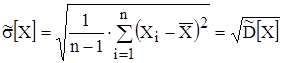 .
.
Оценка с.к.о. среднего арифметического с. в. Х
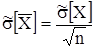 .
.
Оценка дисперсии с. в. 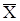
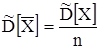 .
.
В ряде задач требуется не только найти для какого-либо параметра его оценку, но и оценить его точность и надежность. Т. е. требуется знать, к каким ошибкам может привести замена параметра его точечной оценкой, и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы.
Такого рода задачи особенно актуальны при малом числе наблюдений, когда точечная оценка в значительной мере случайна и приближенная замена может привести к серьезным ошибкам.
Иными словами, необходимо для полученной оценки найти доверительный интервал для заданной доверительной вероятности.
В качестве примера рассмотрим задачу о доверительном интервале для математического ожидания.
Пусть произведено n независимых опытов над случайной величиной Х, характеристики которой – математическое ожидание m и дисперсия D неизвестны. Для этих параметров получены оценки:
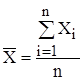 ;
;

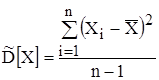 .
.
Требуется построить доверительный интервал 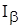 , соответствующий доверительной вероятности
, соответствующий доверительной вероятности 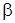 , для математического ожидания m величины Х.
, для математического ожидания m величины Х.
При решении этой задачи воспользуемся тем, что величина 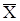 представляет собой сумму n независимых одинаково распределенных случайных величин
представляет собой сумму n независимых одинаково распределенных случайных величин 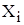 , и, согласно центральной предельной теореме, при достаточно большом n её закон распределения близок к нормальному. На практике даже при относительно небольшом числе слагаемых (порядка 10-20) закон распределения суммы можно приближенно считать нормальным.
, и, согласно центральной предельной теореме, при достаточно большом n её закон распределения близок к нормальному. На практике даже при относительно небольшом числе слагаемых (порядка 10-20) закон распределения суммы можно приближенно считать нормальным.
Будем исходить их того, что величина 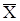 распределена по нормальному закону. Характеристики этого закона – математическое ожидание и дисперсия – равны соответственно
распределена по нормальному закону. Характеристики этого закона – математическое ожидание и дисперсия – равны соответственно 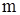 и
и 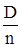 .
.
Предположим, что величина D известна, найдём такую величину 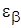 для которой:
для которой:
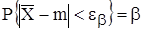 .
.
Выразим вероятность в левой части этого выражения через нормальную функцию распределения (интеграл Лапласа):
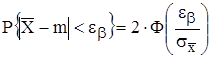 .
.
Где 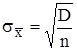 - среднее квадратическое отклонение оценки
- среднее квадратическое отклонение оценки 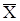 .
.
Из уравнения:
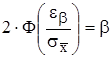 .
.
Находим значение 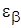 :
:
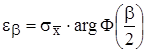 .
.
Где 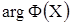 - функция обратная
- функция обратная 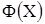 .
.
Дисперсия D, через которую выражена величина 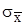 нам в точности неизвестна, в качестве её ориентировочного значения можно воспользоваться оценкой
нам в точности неизвестна, в качестве её ориентировочного значения можно воспользоваться оценкой 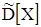 и положить приближенно:
и положить приближенно:
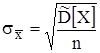 .
.
Обозначить через:
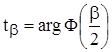 .
.
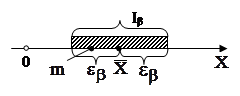
Тогда доверительный интервал можно представить в виде:
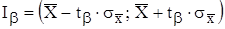 .
.
Пример.
Произведено 20 опытов над величиной 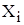 . В результате были получены следующие оценки:
. В результате были получены следующие оценки:
Для математического ожидания: 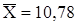 ;
;
Для дисперсии: 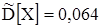 ;
;
Для с.к.о. 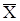 :
: 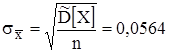 .
.
Требуется построить доверительный интервал соответствующий доверительной вероятности 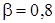 .
.
Учитывая, что при 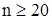 закон распределения близок к нормальному, из таблицы для значений функции Лапласа для
закон распределения близок к нормальному, из таблицы для значений функции Лапласа для 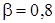 находим
находим 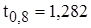 .
.
Отсюда 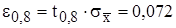 .
.
Тогда доверительный интервал:
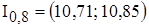 .
.
 2014-01-31
2014-01-31 1275
1275
