Anisotropy in the cosmic background

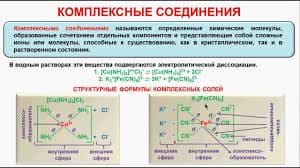
13 It is most useful to describe the CMB anisotropy on the celestial sphere by spherical-harmonic multipole moments,

                            ΔТ(Ө, ф)/Т =Σ a _lm Υ _lm (Ө, ф)

14 The multipole moments, which are determined by the underlying density perturbations, can only be predicted statistically. Averaged over all observers in the universe, they have zero mean; that is to say, <a_lm> = 0. If the underlying density fluctuations are described by a gaussian random process, as inflationary cosmology predicts,the angular power spectrum, C_l≡ <|a_im|²>, contains all possible information. (This is an anverage over all m for agiven ℓ, there being no preferred direction in the uni­verse.) If the density fluctuations are nongaussian, as other models predict, then higher-order correlation func­tions contain additional information.

15 Temperature differences between points on the sky separated by an angle θ are related to those multipoles with spherical-harmonic indices ℓnear 100°/θ. The rms fractional temperature fluctuation for a given angular separation is then

                         (∆T/T)_θ ≈ ℓ(ℓ + l)C_ℓ/2π

The angle θ subtends a length on the surface of last scattering that would now, by the Hubble expansion of the universe, be about 200 megaparsecs per degree. (1 Mpc = 3 x 10⁶ light-years.) Therefore, the correspond­ing ℓ th multipole is determined by density fluctuations on that wavelength scale. For example, the density fluctua­tions of wavelength around 2 Mpc, which seed galaxies, subtend an angle θ of about an arcminute; those of 20 Mpc, which seed clusters of galaxies, subtend about 10 arcminutes; and those of around 200 Mpc, which seed the largest structures we see today, subtend about 1degree. (All these distances were a thousand times smaller at the time of last scattering, when the linear size of the universe was a thousand times smaller. But it is conventional to quote "comoving separations" as they would be now.)

16 The two competing models for the origin of the pri­meval density perturbations involve the physics of the early universe. The first holds that about 10^-32 of a second after the Big Bang, a very short burst of tremendous expansion (called inflation) stretched quantum fluctuations on subatomic scales to astrophysical size, and that those fluctuations became density perturbations when the vacuum energy that drove inflation decayed into radiation and mat­ter. According to this inflationary scenario, the density perturbations are almost scale-invariant: That is to say, fluctuations in the gravitational potential were of the same magnitude (a part in 10⁵) on all length scales. Figure 2 shows the angular power spectrum predicted by inflation.

17 The competing theory holds that the density pertur­bations were seeded by topological defects formed even earlier (10^-36 s), in a cosmological phase transition asso­ciated with spontaneous symmetry breaking in the theory that unifies the fundamental forces and particles. De­pending upon how the symmetry is broken, these defects might be pointlike (global monopoles), one-dimensional (cosmic strings) or three-dimensional (spacetime textures).

It is the gravitational effects of such defects that would induce perturbations thousand of years later in the matter distribution. Although these perturbations would also be approximately scale-invariant, the power spectrum of CMB anisotropy would be very different from what we expect from inflation, because the density perturbations would have originated so much later than in the infationary scenario. The current anisotropy data appear to be consistent with inflation and inconsistent with the topo-logical-defect scenario. (See figure 2.)

18 The inflation and defect models both require non-baryonic dark matter. So do the dynamical measurements of galaxies and clusters that tell us there is much more gravitating matter than can be accounted for by luminous

figure 2. angular power spectrum of CMB temperature fluctuations. The spherical-harmonic multipole number l is conjugate to the separation angle θ ≈100°/ l. The data points thus far favor the theoretical expectations for inflation + cold-dark matter (upper curve) over those for topological-defect theories (lower curve, provided by U. Seljak).

objects, or even by dark baryons. The notably successful theory of Big-Bang nucleosynthesis constrains the baryon density to be less than 10% of the "critical mass density" below which the Hubble expansion would eventually be­come a contraction. But the dynamical observations in­dicate that dark matter contributes at least 20% of this critical density, and inflation favors precisely the full critical density. The observed level of CMB anisotropy provides additional circumstantial evidence: If there were only baryons, the level of primeval inhomogeneity required to produce the observed structure would lead to an an­isotropy ten times greater than we find. (See box 1.)

19 The nonbaryonic matter may be "cold" (slow moving) or "hot" (fast). If most of the dark matter is cold, then structure forms hierarchically—from galaxies to clusters of galaxies to super clusters. If, on the other hand, it's mostly hot, then superclusters would have formed first and then fragmented into clusters and galaxies. There is now good evidence that galaxies formed first (most of them at redshifts of 2 to 3—that is to say, when the universe was a third, or a fourth, of its present linear size), and that clusters and superclusters formed later. That strongly favors the cold-dark-matter picture. (See the article by Henry Ferguson, Robert Williams and Lennox Cowie in physics today, April 1997, page 24.) Together with the measure­ments of CMB anisotropy, the evidence of hierarchical for­mation has made "inflation + cold dark matter" the working hypothesis for how structure formed in the universe.

20 The precise shape of the angular power spectrum depends not only on the underlying inflation model, but also, in a well-understood way, on cosmological parameters such as the Hubble constant, the mass density and the composition of the dark matter. (See box 2.) Therefore, the 2500 or so independent multipoles that can be meas­ured have enormous potential to determine cosmological parameters and test theories of the early universe.