Box 2. The Physics of CMB Anisotropy

 

Temperature fluctuations in the CMB arise from the variations in the matter density. After last scattering, the photons stream freely to us and the temperature fluctuations are seen as CMB temperature differences across the sky. Anisotropy on a given angular scale is related to density perturbations with wavelengths correspending to the length projected by that angle on the last-scattering surface. Until the ions and electrons "recombined" at last scattering, they were tightly coupled to the photons by Thomson scattering; together they behaved as a single fluid. The gravity-driven collapse of a baryon-density perturbation is resisted by the restoring pressure of the photons. Fourier mode k of the temperature fluctuation is governed by a harmonic-oscillator-like equation,

                                                        K²

                                [m_eff Δ T_k'] + 3 ΔT_k = -F_k

 

where F is the gravitational forcing term due to the dark matter, m_eff describes the inertia of the fluid and the primes denote derivatives with respect to (conformal) time. The solutions are acoustic waves.

The large-angular-scale (Sachs- Wolfe) plateau in the angular power spectrum below   ℓ ≈100 (see figure) arises from perturbations with periods longer than the age of the universe at last scattering. CMB photons lose energy climbing out of the potential wells associated with these long-wavelength density perturbations, and the temperature differences seen on the sky reflect the gravi­tational potential differences on the last-scattering sur­face. If the density fluctuations are scale-invariant, the Sachs- Wolf plateau is flat.

The baryon-photon fluctuations that produce anisotropy on subdegree angular scales (10²< ℓ <10³) have time enough to oscillate. At maximum (minimum) com­pression, the CMB temperature is higher (lower) than average; neutral compression corresponds to maximum fluid velocity, which leads to a Doppler-shifted CMB temperature. Because last scattering is nearly instantane­ous, the CMB provides a snapshot of these acoustic oscillations, with different wavelength modes caught in different phases. Because a given multipole ℓ is domi­nated by the effects of a narrow band of Fourier modes (k≈H₀l/2), this leads to peaks and valleys in the angular power spectrum. The peaks are modes that were maximally under- or overdense at last scattering, and the troughs are velocity maxima in between.

On the smallest scales (ℓ > 2500), the spectrum is exponen­tially damped, due to the finite thickness of the last-scattering surface. Features on these angular scales are washed out because last scattering here is a montage of snapshots, which blurs the fine details.

The precise shape of the power spectrum depends on cosmological parameters as well as the underlying density pertur­bations. Thus, it encodes a wealth of information. (See the figure.) The position of the first peak is sensitive to the total energy density, and it can be used to determine the geometry of the universe: ℓ_peak ≈ 200/ √ Ω. It moves to smaller angles as Ω decreases because the distance to the last-scattering surface increases (the Hubble expansion decelerates less in a low-density universe) and geodesies diverge in negatively curved space, so that a given distance on the last-scattering surface subtends a smaller angle).

Other features encode other information. For example, the height of the first peak depends on the baryon and total matter densities (both of which both depend on H₀) and a possible "cosmological constant." What if the spectrum of density perturbations is not scale-invariant? If, for example, there is more power on smaller scales (n > 1), the angular power spec­trum rises with increasing ℓ.

 

Mean square temperature fluctuation

MULTIPOLE /

 

dependence of the angular power spectrum of CMB

temperature fluctuations on cosmological and model parameters. From red to green to blue: (top panel) power-law index n = 1, 1.1 and 1.2; (2nd panel) Hubble constant H₀ — 50, 60 and 70 km/(s Mpc); (3rd panel) density parameter Ω, = 1, 0.5 and 0.3; (bottom panel) Ω (the baryon fraction of critical density) = 0.005, 0.0075 and 0.01.

 

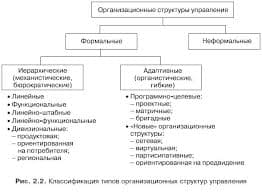
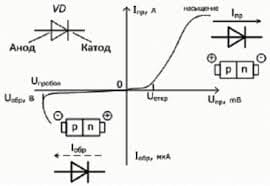
IV. Reading for General Understanding

A Check the comprehension of the texts in Box 1 and Box 2 by choosing the answer, which you think, is correct.

 

1. The expansion of the universe is described by the cosmic linear-scale factor R(t).

- You are mistaken. It is the compression of the universe is described by the cosmic linear-scale factor R(t).

- You are quite right. It is the expansion of the universe is described by the cosmic linear-scale factor R(t).

- It is not true. The expansion of the universe is described by the angular scale factor.

2. A critical universe is spatially flat.

- No, it is not. It is negatively curved.

- You are right. The critical universe is spatially flat.

- You are mistaken. The critical universe is negatively curved like a saddle.

 

3. The expanding universe cools adiabatically with temperature falling like 1/R(t).

- Yes, that’s right. The expanding universe cools adiabatically.

- You are wrong. It doesn’t cool adiabatically. It cools giving the heat off.

- You can’t be sure of it. The expanding universe cannot cool adiabatically.

 

4. This “recombination” drastically and suddenly reduced and suddenly reduced the Thompson-scattering opacity.

- You are completely mistaken.

- You are absolutely wrong. This “recombination” reduced the Thompson-scattering opacity very slowly.

- To my mind, you are quite right. This “recombination” reduced drastically.

5. The gravity-driven collapse of a baryon – density perturbation is resisted by the restoring pressure of the photons.

- The gravity-driven collapse is eliminated by the restoring pressure of the photons.

- The gravity-driven collapse is facilitated by the restoring pressure of the photons.

- The gravity-driven collapse is resisted by the restoring pressure of the photons.

 

6. The precise shape of the power spectrum depends on cosmological parameters as well as the underlying density perturbations.

- The precise shape of the power spectrum depends on cosmological parameters as well as the restoring pressure of the photons.

- The precise shape of the power spectrum as well as the underlying density perturbations depend on cosmological parameters.

- The precise shape of the power spectrum does not depend on cosmological parameters and the underlying density perturbations either.

 

 

B Pick out from the text all the word combinations with the following words and give their Russian equivqlents.

 

- density                                   - scale

- perturbation(s)                       - galaxy

- universe                                 - size

- matter                                    - spectrum

- cluster(s)                               - scattering

 

V. Reading for Detail and Language Study

 

A Find in the whole text the English equivalents for the following phrases.

 

Большой взрыв, галактика, звёзды, материя, периодическая система, тёмная материя, чёрное тело, пустота, кластер, оценка, доля градуса, наблюдатели, непреодолимый, действие силы тяжести, испытание (проверка) моделей, небесная сфера (небосвод), вселенная, дополнительная информация, рассеяние, колебания плотности, длина волны, очень короткий взрыв, энергия вакуума, основные силы и частицы, нарушать симметрию, скорость расширения.

 

 

B Translate the following sentences from English into Russian

1. Averaged over all observers in the universe, they have zero mean, that is to say <a_lm>=0

2. This is an average over all m for a given l, there being no preferred direction in the universe.

3. They estimated the temperature to be isotropic within about 10%.

4. The current anisotropic data appear to be consistent with inflation and inconsistent with the topological – defect scenario.

5. It is gravitational effects of such defects that would induce perturbations thousands of years later in the matter distribution.

6. If there were only baryons, the level of primeval inhomogeneity, required to produce the observed structure, would lead to an anisotropy ten times greater than we find.

7. That strongly favors the cold-dark-picture.

8. If, on the other hand, it’s mostly hot, then superclusters would have formed first and then fragmented into clusters and galaxies.

9. Therefore the 2500 or so independent multipoles that can be measured have enormous potential to determine cosmological parameters and test theories of the early universe.

10. That is to say: fluctuations in the gravitational potential were of the same magnitude on all length scale.

 

C Translate the text in Box 2 in written form

 

 

VI. Oral Phractice

A Answer the questions on the text “The Cosmic Rosetta Stone”

 

1. Where is baryonic matter found?

2. What is the universe characterized by today?

3. What colour is the matter in the universe?

4. Is the composition of the matter known?

5. What was the composition of the universe during its earliest moments?

6. What serves as a cosmic Rosetta stone?

7. In what way was the CMB found and when?

8. What scientists began to interpret the Big Bang?

9. What nuclei were made in the Big Bang?

10. What is the COBE?

11. Who began

ics

 

I. Answer the following question

 

1. What describes the expansion of the universe?

2. What is the shape of a low-density universe?

3. When do the wavelengths of photons stretch?

4. In what way does the expanding universe cool?

5. When did the CMB photon experience their last scattering?

6. What does this extra early growth of density perturbations mean?

 

 

B Render the text of Box 2

 

The Scientific Harvest

Translate into English

1. Сколько экспериментов обнаружили анизотропию на угловых шкалах?

2. Все эти эксперименты были менее точны, чем СОВЕ.

3. Эти эксперименты добавили многое к нашему пониманию анизотропии.

4. Эти эксперименты снизили ценность моделей с топологическими дефектами.

5. Новое поколение приборов было установлено на зондах, находящихся в воздухе длительное время.

6. Приборы, установленные на Южном полюсе и в пустыне Чили, будут определять важные «акустические пики» в многополюсном спектре.

7. Низкочастотные приёмники будут определять спектр угловой мощности.

8. Два искусственных спутника определят 2500 мультиполюсов.

9. Теоретически, спектр угловой мощности зависит от приблизительно 10 параметров.

10. Поэтому теорию можно проверить очень тщательно (всесторонне).

 

 

 

BOX II The Physics of CMB Anisotropy

    

Translate into English

1. Колебания температуры возникают из-за изменений в плотности материи.

2. Ионы и электроны были жестко связаны с фотонами посредством томсоновского рассеяния.

3. Этот параметр описывает инерцию текучей среды.

4. При максимальном сжатии температура СМ выше средней.

5. Последнее рассеяние было почти мгновенным.

6. Пики - это моды, которые были максимально плотными при последнем рассеянии.

7. Точная конфигурация энергетического спектра зависит от космологических параметров.

8. Позицию первого пика можно использовать для определения геометрии вселенной.