Моменты случайной величины

 

41.1. Математическое ожидание и дисперсия являются примерами моментов случайной величины, которые определяются следующим образом.

Начальным моментом порядка  непрерывной случайной величины с плотностью распределения вероятности  называется число

    .                            (41.1)

Порядок момента  - это неотрицательное целое число, т.е. .

Начальным моментом порядка  дискретной случайной величины , принимающей значения  с вероятностями , , называется число

    .                                  (41.2)

Определение (41.1) можно рассматривать как универсальное определение для непрерывных и для дискретных случайных величин. В последнем случае плотность вероятности выражается через  - функцию согласно формуле (34.4). Однако на практике для вычисления момента дискретной величины удобнее использовать соотношение (41.2).

Центральным моментом порядка  случайной величины  называется число

    .                                       (41.3)

Для непрерывной случайной величины  с плотностью вероятности  центральный момент порядка  имеет вид:

    .                      (41.4)

41.2. Из всего множества начальных и центральных моментов обычно используются моменты невысоких порядков, до  включительно, как более простые характеристики случайной величины. Применение моментов высоких порядков, , ограничено. Во-первых, при больших  моменты могут не существовать, поскольку могут расходиться интегралы (41.1), (41.4). И во-вторых, интерпретация моментов высших порядков затруднена.

Рассмотрим начальные моменты, начиная с . При этом из (41.1) следует

    .                          (41.5)

Итак, начальный момент нулевого порядка  для любой случайной величины, следовательно, этот момент не отражает каких-либо свойств случайной величины, т.е. не является ее характеристикой. При  из (41.1) следует, что момент первого порядка - это математическое ожидание случайной величины. Разные случайные величины могут иметь разные математические ожидания, и поэтому число  является характеристикой случайной величины: число  указывает положение центра ее плотности вероятности.

Момент второго порядка

                                      (41.6)

- это среднее квадрата  случайной величины, и т.д.

Рассмотрим аналогично центральные моменты (41.4). При  получаем  - одинаковый результат для любой случайной величины. Поэтому данный момент не является характеристикой случайной величины, поскольку не отражает каких-либо ее свойств. При   . Этот результат также одинаков для любой случайной величины, поэтому центральный момент первого порядка не является характеристикой случайной величины. При  из (41.4) получаем дисперсию

                          (41.7)

- важнейшую числовую характеристику случайной величины и т.д.

Моменты третьего и четвертого порядков будут рассмотрены в дальнейшем.

 

Неравенство Чебышева

 

42.1. Пусть случайная величина  имеет конечный момент второго порядка , тогда

    ,                           (42.1)

где  - любое действительное число и . Соотношение (42.1) называют неравенством Чебышева.

Сначала рассмотрим доказательство неравенства, следующего из (42.1) при :

    .                                         (42.2)

Доказательство неравенства Чебышева удобнее рассматривать отдельно для непрерывной и для дискретной случайных величин. При этом доказательства являются относительно простыми, а ход доказательств вполне очевиден. В то время как универсальное доказательство, справедливое и для непрерывной и для дискретной случайных величин оказывается значительно более сложным. Рассмотрим непрерывную случайную величину  с плотностью вероятности . Тогда в соотношении    первое слагаемое можно представить в виде

,

поэтому

.

Здесь использовано неравенство  - справедливое на области интегрирования. Полученное выражение совпадает с неравенством (42.2). Аналогично выполняется доказательство для дискретной случайной величины.

Теперь случайную величину  в (42.2) можно заменить на случайную величину , где  - любое действительное число, тогда из (42.2) следует неравенство Чебышева (42.1). Это неравенство определяет границу сверху для вероятности  или, как говорят, больших уклонений  случайной величины  от числа . Большие уклонения понимаются в смысле их превышения над заданным числом .

42.2. Пусть , тогда неравенство Чебышева (42.1) имеет вид

    .                          (42.3)

Теперь минимальное уклонение  можно измерять в единицах среднеквадратического уклонения  случайной величины , т.е. положить

    ,                                        (42.4)

где  - коэффициент пропорциональности. Подставим (42.4) в (42.3), тогда

    .                             (42.5)

Если правая часть , то (42.5) не представляет какого-либо ограничения на случайную величину, поскольку вероятность  не может выходить за пределы интервала . Поэтому коэффициент  в (42.5) имеет смысл рассматривать только большим: . Отсюда очевидна интерпретация неравенства Чебышева как неравенства, определяющего границу сверху вероятности больших уклонений.

Пусть  - непрерывная случайная величина с плотностью вероятности 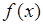, тогда неравенству Чебышева (42.1) можно дать простую геометрическую интерпретацию, представленную на рис. 42.1.

 

Рис. 42.1. Иллюстрация к неравенству Чебышева.

 

Здесь указаны числа ,  и , заштрихованная площадь - это вероятность

 

.