Для нахождения разности векторов приведём

их к общему началу. Соединив их концы, построим треугольник. Тогда имеем .

Отсюда легко можно получить правило для нахождения суммы большего числа векторов.

 Сумму нескольких   векторов можно найти по правилу многоугольника: чтобы найти вектор, представляющий собой сумму заданных векторов, нужно последовательно совместить начало следующего вектора-слагаемого с концом предыдущего, тогда вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего, будет суммой заданных векторов.   

Например, вектор    есть сумма заданных векторов  и :

.

Свойства сложения векторов:

1) – переместительное св-во (коммутативность);  

2)    – сочетательное св-во (ассоциативность). Оба свойства операции сложения векторов следуют непосредственно из определения операции.

Для любых двух векторов   и  справедливо неравенство треугольника:  (если векторы  и  неколлинеарны, то сумма длин двух его сторон больше длины третьей стороны). Очевидно, что это неравенство выполняется и для любого числа векторов, т.е. .

 

Умножение вектора на скаляр.

 

Пусть  – ненулевой вектор,  – скаляр. 

Произведением   вектора  на скаляр   называется вектор , обладающий следующими свойствами:

а) , ;

б) , т.е. они коллинеарны;

в) сонаправлен вектору   (т.е. направлен одинаково с ним), если , и направлен в противоположную сторону, если .

Замечание. Из определения следует, что

1. вектор    нулевой, если один из его сомножителей равен нулю;

2. критерий коллинеарности двух векторов:

если , при   (существует такое ).

 

Свойства   умножения вектора на скаляр:

1. Перестановочное (или коммутативное)

2. Сочетательное (или ассоциативное): , где  - скаляры.

3. Распределительное (дистрибутивное):

, где  и  - скаляры;

.

Доказательства этих свойств непосредственно вытекают из определения равенства векторов и сложения векторов.

3.   Линейная зависимость и независимость векторов.  

Пусть даны векторы   и скаляры .

Определение 1. Вектор

называется линейнойкомбинацией векторов .

Определение 2.

Векторы называются линейно независимыми, если равенство

выполняется только  при условии, что   при всех

(только при нулевом наборе коэффициентов ).

Определение 3.

Векторы называются линейнозависимыми, если их линейная комбинация обращается в ноль при условии, что хоть один  из скаляров    отличен от нуля.

Это значит, что среди всех наборов коэффициентов , при которых линейная комбинация обращается в ноль, есть хоть один ненулево й.

Замечание. 

Пусть , а какой-то  отличен от нуля. Например, пусть . Тогда имеем

.

Следовательно, если система векторов линейно зависима, то, по крайней мере, один из векторов этой системы  есть линейная комбинация остальных векторов.

Поэтому любые два коллинеарных вектора () линейно зависимы, и любые три компланарных вектора () тоже линейно зависимы. 

Справедливы и обратные утверждения: любые два неколлинеарных вектора на плоскости линейно независимы и любые три некомпланарных вектора в пространстве линейно независимы.  

Действительно, если ненулевые векторы  и   неколлинеарны, то из  следует . Иначе есть ненулевой набор коэффициентов , что противоречит предположению о неколлинеарности.

Еслиже три ненулевых вектора  и   некомпланарны (два вектора всегда компланарны), то из равенства   следует, что . Иначе опять придём к противоречию: 

если, например, , то   и по определению операции сложения векторов данные вектора  и   образуют  треугольник, через который можно провести плоскость.

 

Определение 4.

Любая пара неколлинеарных векторов на плоскости и любая тройка векторов в пространстве называется базисом множества всех векторов, расположенных соответственно на плоскости или в пространстве.

Сами эти векторы называют базисными векторами.

 

Из замечания следует, что, если два компланарных вектора  и    не коллинеарны,то любой третий вектор , компланарный с ними, можно представить в виде , т.е., как говорят, можно разложить по базису (, 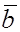). Числа  и   в этом случае называются координатами вектора   в базисе (, ).. Разложение вектора  по базису (, 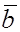) единственно, т.е. координаты  и  можно найти единственным образом. Покажем это.

Действительно. Пусть заданы векторы , причем  и 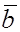 неколлинеарны. Если вектор  коллинеарен одному из векторов, например, вектору , тогда   или , где .

Если вектор  неколлинеарен ни одному из векторов  и 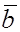, то приведём вектора   к одному началу . Продолжим прямые, на которых лежат вектора  и , а затем проведем прямые, параллельные векторам   и  через конец вектора , достроив таким образом параллелограмм OPQR.. Вектор  является диагональю параллелограмма. Тогда по правилу параллелограмма имеем , но

Из построения следует и единственность такого разложения вектора по базису . Количество базисных векторов называется размерностью векторного пространства: так плоскость называется двумерным пространством и обозначается .

Любые три некомпланарных вектора , ,  в пространстве линейно независимы и образуют базис трехмерного пространства ; всякийчетвертый  вектор  этого пространства можно единственным образом разложить по базису (, , 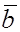), т.е. представить в виде , где a, b, g – координаты вектора   в базисе (, , ),.

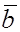Доказательство  можно провести аналогично предыдущим рассуждениям.

Определение 5.

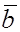Три некомпланарных вектора , ,   называются правой тройкой векторов, если из конца третьего вектора () кратчайший поворот от первого вектора () ко второму вектору () виден происходящим

 в положительном направлении (против часовой стрелки).

И, соответственно, – левой тройкой, если по часовой стрелке.