2020-04-12
94
Означення 10
Мінором r-го порядку матриці А розмірів m x n називається визначник r-го порядку, утворений з елементів матриці А, що залишились після викреслення в ній m-r рядків і n-r стовпців (r 
m, r n).
Означення 11
Натуральне число r називається рангом матриці А, якщо воно задовольняє такі вимоги:
1. Матриця А має мінор r-го порядку, відмінний від нуля;
2. Усякий мінор (r+1)-го і більш високого порядку (якщо такі існують) дорівнює нулю.
Означення 12
Елементарними перетвореннями матриці називають такі операції:
1. Перестановка (транспозиція) двох рядків або стовпців;
2. Додавання до всіх елементів рядка (стовпця) відповідних елементів другого рядка (стовпця), помножених на деяке число.
Матриці, здобуті одна з іншої за допомогою скінченого числа елементарних перетворень, називаються еквівалентними.
Теорема 1
Ранги еквівалентних матриць рівні.
Означення 13
Матриця розмірів m х n, рангу r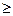 
1 називається трапецієподібною, якщо існує таке натуральне число l (l 
), що
1. Елементи а 11, а 22,... аll не дорівнюють нулю;
|
|
|
2. Якщо l<m, то елементи стовпців, що стоять під елементами а 11, а 22, а 33, ... а ln , дорівнюють нулю; якщо l=m, то дорівнюють нулю елементи стовпців, що стоять під елементами а 11, а 22,... а l-1l-1. Трапецієподібна матриця має вигляд
Теорема 2
Ранг трапецієподібної матриці дорівнює кількості ненульових рядків. 
Обчислення рангу матриці способом знаходження елементарними перетвореннями еквівалентної даній трапецієподібної матриці.
Приклад 6
Обчислити ранг матриці А= 
.
Виконаємо такі елементарні перетворення матриці А. Переставимо місцями 1-й і 3-й стовпці матриці А, отримаємо:
.
Додамо до елементів 2-го рядка елементи 1-го, а до третього елементи 1-го рядка, помножені на число – 5, тоді матимемо:
.
Додаючи до елементів 3-го рядка елементи другого, помножені на 3, дістанемо:
.
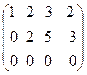Здобули трапецієподібну матрицю, для якої 
. Отже, r(A) = 2.
Означення 14
Квадратна матриця С порядку n називається оберненою до матриці А, якщо АС=СА=Е, де Е – одинична матриця n- го порядку. Матриця, обернена до матриці А позначається через А-1. Квадратна матриця А порядку n називається особливою, якщо її детермінант дорівнює нулю. Якщо 
0, то А називається неособливою.
Теорема 3
Особливі матриці обернених не мають. Кожна неособлива матриця має обернену матрицю, що обчислюється за формулою:
А- 1 = 
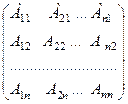, де Аij 
–
алгебраїчне доповнення елемента аij матриці А.
Приклад 7
Для даної матриці А= 
знайти обернену і виконати перевірку.
1. Обчислимо визначник даної матриці.
= 
=2 
- 3 
+ 5 
= 2(5–9) –3(20– –9)+5(12–3)=–8–33+45=4, як бачимо 
, тому існує обернена матриця.
|
|
|
2. Знайдемо алгебраїчні доповнення елементів даної матриці.
А 11= (–1)1+1 = 5–9 = –4.
А 12= (–1)1+2 = – (20–9) = –11.
А 13= (–1)4 =12–3 =9.
А 21= (–1)3 
= – (15–15) =0.
А 22 = (–1)4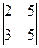 
= (10–15) =–5.
А 23 = (–1)5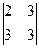 
= – (6–9) =3.
А 31 = (–1)4 
= 4.
А 32 = – (–14) =14.
А 33 = –10.
3. Запишемо обернену матрицю за формулою:
А -1 =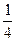 
4. Перевірка. А -1∙ А =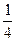 
=
= 
= = 
= 
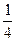
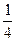
= Е.
