Понятие продолжимости решения. Признак Винтера-Еругина

Пусть

--- решение системы уравнений, определенное на некотором интервале , и

--- решение той же системы уравнений, определенное на некотором интервале . Будем говорить, что решение является продолжением решения, если . Решение будем называть непродолжаемым, если не существует никакого отличного от него решения, являющегося его продолжением.

Покажем, что каждое решение может быть продолжено до решения, далее непродолжаемого. В этом смысле непродолжаемые решения исчерпывают совокупность всех решений.

Пусть

--- векторная запись нормальной системы уравнений. Тогда справедлива следующая теорема:

Теорема 1. Существует непродалжаемое решение уравнения с произвольными начальными значениями из .

2. Если некоторое непродолжаемое решение уравнения совпадает с некоторым другим решением уравнения, хотя бы при одном значении 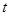, то оно является продолжением этого решения.

3. Если два непродолжаемых решения уравнения совпадают между собой хотя бы для одного значения 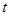, то они полностью совпадают, т.е. имеют один и тот же интервал определения и равны на нем.

Пусть --- решение системы с начальным условием . Ясно, что:

а) либо это решение может быть продолжено для всех значений , и тогда будем говорить, что решение неограниченно (бесконечно) продолжаемо [в право];

б) либо существует такое , что при , и тогда будем говорить, что решение имеет конечное время определения.

Эти две возможности явно несовместимы и дополняют друг друга. Третий случай

в) решение ограничено.

--- совместим с возможностью а), но, конечно, несовместим с б).

Отметим, следующее

Свойство Если решение ограничено в своем максимальном промежутке существования , то оно бесконечно продолжаемо, т.е. .

Ограниченность всех решений представляет собой своего рода устойчивость; в этом случае говорят об устойчивости в смысле Лагранжа или, короче, об устойчивости по Лагранжу.

Неограниченная продолжимость решений системы является необходимым условием устойчивости по Ляпунову решений этой системы.

Пример