2020-06-29
133
ПРАКТИЧЕСКОЕ ЗАДАНИЕ №4
(ДИСТАНЦИОННОЕ ОБУЧЕНИЕ)
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ОТ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ
Основные понятия
6.1.1. Определение. Если функция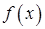 
непрерывна при 
и в точке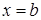 
имеет бесконечный разрыв, то несобственным интегралом 
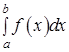называется 
.
Если предел существует и конечен, то несобственный интеграл называется сходящимся, если предел не существует или бесконечен, то интеграл называется расходящимся.
6.1.2. Определение. Если функция 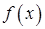непрерывна при 
и в точке 
имеет бесконечный разрыв, то несобственным интегралом 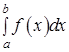называется 
.
Если предел существует и конечен, то несобственный интеграл называется сходящимся, если предел не существует или бесконечен, то интеграл называется расходящимся.
6.1.3. Определение. Если функция 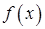непрерывна при 
и в точке 
имеет бесконечный разрыв, то несобственным интегралом 
называется сумма несобственных интегралов 
.
Если оба интеграла в правой частисходятся, то несобственный интеграл называется сходящимся, если хотя бы один из интегралов расходится, то интеграл называется расходящимся.
|
|
|
6.1.4. Определение. Если функция 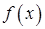непрерывна при 
, а в точках и 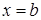имеет бесконечные разрывы, то несобственным интегралом 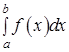называется сумма несобственных интегралов 
, где 
внутренняя точка промежутка 
.
Если оба интеграла сходятся, то несобственный интеграл называется сходящимся, если хотя бы один из интегралов расходится, то интеграл называется расходящимся.
Вычисление несобственных интегралов от неограниченных
Функций или установление их расходимости
Формула Ньютона-Лейбница для несобственных интегралов от неограниченных функций.
1) Если функция 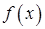непрерывна при 
, а в точке имеет бесконечный разрыв, то 
, где 
2) Если функция 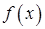непрерывна при 
, а в точке имеет бесконечный разрыв, то 
, где 
(ср. п. 1.2.8).
3) Если функция 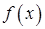непрерывна при 
, а в точке имеет бесконечный разрыв, то
, где 
и 
вычисляются соответственно по формуле 1) и по формуле 2).
4) Если функция 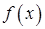непрерывна при , а в точках и 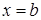имеет бесконечные разрывы, то
, где и вычисляются соответственно по формуле 2) и по формуле 1).
