Метод малого параметра

 

Нелiнiйна механiчна система називається автономною, якщо її рух описується диференцiальним рiвнянням, яке явно не залежить вiд часу. Наприклад:

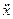+k ² x = μf (x, ),                       (6.22)

де μ - деякий параметр, f (x, ) - неперервна нелiнiйна диференцiйована функцiя.

Знайдемо перiодичний розв’язок рiвняння (6.22) в припущеннi, що параметр μ є малою величиною, а функцiя f (x, ) залежить тiльки вiд х. Використаємо метод розкладання в ряд по степенях малого параметра μ i запишемо шуканий розв’язок у виглядi:

x = x ₀ +μx ₁ +μx ₂ +…,                     (6.23)

де x ₀, x ₁, x ₂ - невiдомi перiодичнi функцiї колової частоти р i частот, кратних р, якi треба знайти. Розкладемо квадрат колової частоти р ² по степенях малого параметра μ:

p ² = k ² +α ₁ μ+ α ₂ μ ² +…,                   (6.24)

де α ₁ i α ₂ - постiйнi коефiцiєнти.

При розв’язуваннi задач методом малого параметра потрiбно дотримуватись такої послiдовностi:

1) скласти диференцiальне рiвняння руху у виглядi

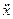+k ² x- μf (x) = 0;                         (6.25)

2) за допомогою формул (6.23) i (6.25) записати шуканий закон руху х i квадрат невiдомої колової частоти р в розкладаннi по степенях малого параметра μ;

3) за допомогою формули (6.23) знайти  i ;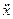

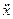4) пiдставити значення х,  i  та

k ² = p ² - α ₁ μ- α ₂ μ ² -...

в формулу (6.25). В результатi пiдстановок одержимо диференцiальне рiвняння з членами, якi утримують рiзнi степенi малого параметра μ, а також з членами без μ;

5) зiбрати в диференцiальному рiвняннi, одержаному в пунктi 4, члени, утримуючi степенi малого параметра μ:

А ₀ +μА ₁ +μ ² А ₂ +... = 0;

6) прирiвняти до нуля коефiцiєнти, якi стоять при рiзних степенях малого параметра μ. В результатi одержимо систему диференцiальних рiвнянь

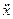₀ +р ² х ₀ = 0;

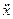₁ +р ² х ₁ = F ₁(α ₁, х ₀);                           (6.26)

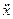₂+ p ² x ₂ = F ₂(α ₁, α ₂, х ₀, х ₁) i т. д.;

7) записати початковi умови руху для диференцiальних рiвнянь, одержаних в пунктi 6. Наприклад, якщо за умовою при t ₀= 0 ми маємо х (0) = а, (0) = 0, то на основi формул для  i  пункту 3 одержимо при t ₀ = 0

х ₀(0) = а,     х ₁(0) = 0,   х ₂(0)= 0, ...

₀(0)= 0,    ₁(0) = 0, ₂(0) = 0, ...;

8) скориставшись початковими умовами, записаними в пунктi 7, потрiбно проiнтегрувати диференцiальне рiвняння 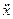₀ +р ² х ₀ = 0 i знайти x ₀(t);

9) внести одержаний вираз для x ₀(t) в диференцiальне рiвняння

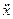₁ +р ² х ₁ = F ₁(α ₁, х ₀),

яке пiсля тригонометричних перетворень записується у виглядi:

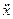₁ +р ² х ₁ = M ₁cos(pt) +N ₁cos(3 t) +….      (6.27)

Для того, щоб x ₁ з часом не зростало до нескiнченностi, треба покласти М ₁ = 0. З рiвняння М ₁ = 0 визначити α ₁;

10) скориставшись початковими умовами руху пункта 7, потрiбно проiнтегрувати диференцiальне рiвняння

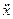₁ +р ² х ₁ = N ₁cos(3 t)+ …

i визначити x ₁(t);

11) пiдставити значення x ₀(t), α ₁ i x ₁(t) в диференцiальне рiвняння

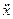₂ +p ² x ₂ = F ₂(α ₁, α ₂, х ₀, х ₁).

Повторивши викладки пунктiв 9 i 10, визначити α ₂ i x ₂(t);

12) визначити x (t) i р ².

При розв’язуваннi задач ряди слiд обiрвати на членах, якi утримують μ i μ ².

 

Зауваження. Для закріплення матеріалу §6 необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 57.3, 57.4;

2) № 57.1, 57.2, 57.5, 57.9;

3) № 57.11, 57.12.

 

§7. Диференцiальнi рiвняння руху невiльної матерiальної точки