2020-10-10
185
Теорема №2. Первое и второе определение предела функции в данной точке эквивалентны.
Доказательство
I. 1. Пусть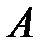 
– предел функции f(x) в точке 
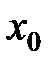согласно первому определению предела функции в точке. Требуется доказать, что число 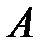- предел функции согласно определения №2.
2. Предположим обратное, что число 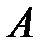не является пределом этой функции согласно определения №2 [2].
3. Это значит, что не для любого 
можно указать такое 
, что из неравенства 
следовало бы неравенство 
. Т. е., сущест- вует такое 
, для которого какое бы 
ни взять, найдётся хоть одна точка 
такая, что 
, но 
.
4. Возьмём в качестве 
последовательно такие числа: 
5. Тогда для 
во множестве X найдётся такая точка 
что
, а 
.
Для 
во множестве X найдётся такая точка 
что 
, а 
;
Для 
во множестве X найдётся такая точка 
что 
,а 
;
…………………………………………………………………………
Для 
во множестве X найдётся такая точка 
, а 
.
…………………………………………………………………………
6. В результате получается последовательность точек, отличных от :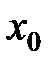 
, сходящаяся к 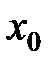, так как разность 
стремится к нулю при 
(
.
7. Тогда согласно первому определению предела функции в точке по Гей не, соответствующая последовательность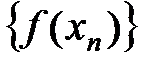 
значений функции схо- дится к числу 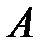, т. е. 
[2].
8. Следовательно, по определению предела последовательности 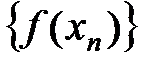по 
найдется такой номер 
, что для всех 
будет выполнятся 
.
9. А по принятому (п.5) должно выполняться неравенство .
10. Полученное противоречие и доказывает, что число 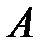является преде- лом функции f(x) в точке 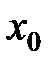согласно определения №2 (по Коши).
II. 1. Пусть дано, что число 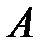– предел функции 
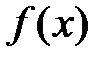в точке 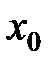по определению №2. Требуется доказать, что число 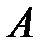- предел функции 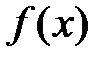по определению №1.
2. Если число 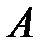- предел функции в точке 
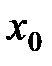согласно определения №2, то 
существует такое 
, что из неравенства 
следует неравенство 
.
3. Возьмём любую последовательность точек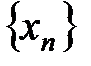 
: 
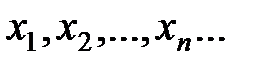, схо- дящуюся к точке , 
.
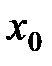4. Тогда согласно определения предела последовательности 
будет выполняться неравенство 
.
5. Вместе с тем в силу второго определения предела функции в точке будет выполняться и 
, .
6. Так как 
выбиралось произвольно, последовательность точек 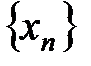выбиралась произвольно, то это означает, что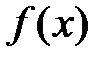 
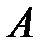для любой 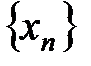, сходящейся к ().
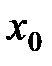7. Таким образом, число 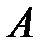является пределом 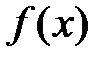в точке 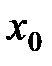согласно первому определению (по Гейне) [2]. Ч.т.д.
Замечание №2 1. Итак, установлена эквивалентность обоих опре- делений предела функции в точке. Можно использовать любое из них в зависимости от того, какое более удобно при решении той или иной задачи.
2. Оба определения сами по себе еще не дают способа отыскания предела данной функции в точке. С их помощью иногда можно установить, будет ли то или иное число пределом функции, или можно убедиться, что данная функция вовсе не имеет предела [15].
