Здесь приводится ряд теорем, имеющих большое теоретическое и прикладное значение.
Теорема 3.1. (Ролля)
Если функция 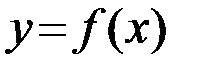 непрерывна на отрезке
непрерывна на отрезке 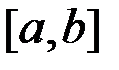 , дифференцируема на интервале
, дифференцируема на интервале 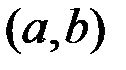 и на концах отрезка принимает одинаковые значения
и на концах отрезка принимает одинаковые значения 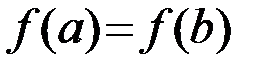 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 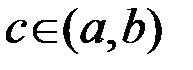 , в которой производная обращается в нуль, то есть
, в которой производная обращается в нуль, то есть 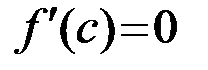 .
.
З а м е ч а н и е 3.1. Производная функции в точке 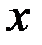 – угловой коэффициента касательной к графику функции
– угловой коэффициента касательной к графику функции  в точке
в точке 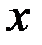 (геометрический смысл производной:
(геометрический смысл производной: 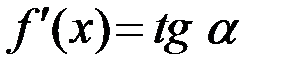 ).
).
Геометрический смысл теоремы Ролля заключается в том, что на графике функции найдется такая точка, в которой касательная параллельна оси 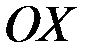 , а именно, точка с координатами
, а именно, точка с координатами 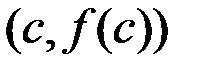 , в которой
, в которой 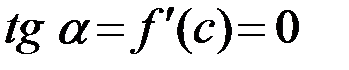 (см. Рис 3.1).
(см. Рис 3.1).
.
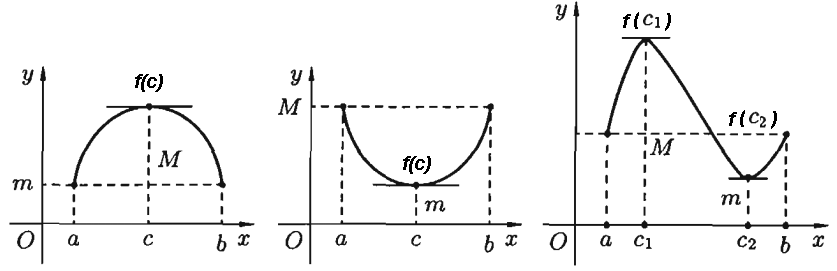
Рис 3.1
Теорема 3.2. (Коши)
Если функции 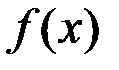 и
и 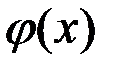 непрерывны на отрезке
непрерывны на отрезке 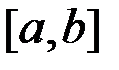 , дифференцируемы на интервале
, дифференцируемы на интервале 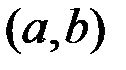 , причем
, причем 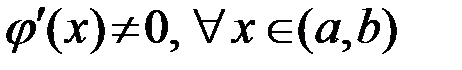 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 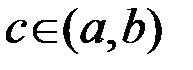 такая, что выполняется равенство
такая, что выполняется равенство 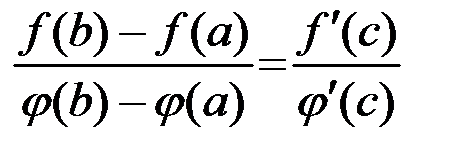 .
.
Теорема 3.3. (Лагранжа)
Если функция 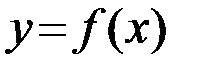 непрерывна на отрезке
непрерывна на отрезке 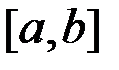 , дифференцируема на интервале
, дифференцируема на интервале 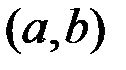 и на концах отрезка принимает одинаковые значения
и на концах отрезка принимает одинаковые значения 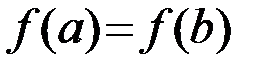 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 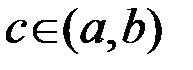 , такая, что выполняется равенство
, такая, что выполняется равенство 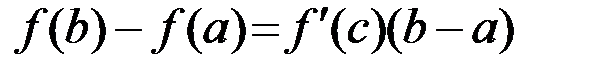 .
.
|
|
|
Полученную в теореме Лагранжа формулу называют формулой конечных приращений или формулой Лагранжа. Если формулу Лагранжа записать в виде 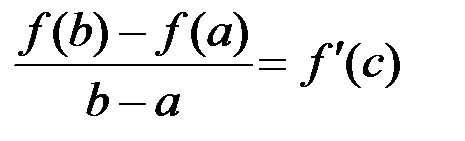 , тотеорема Лагранжа принимает простой геометрический смысл: на графике функции
, тотеорема Лагранжа принимает простой геометрический смысл: на графике функции 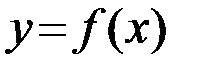 найдется точка
найдется точка 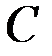 , с координатами
, с координатами 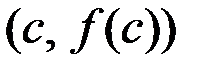 , в которой касательная параллельна секущей – прямой, проходящей через точки
, в которой касательная параллельна секущей – прямой, проходящей через точки 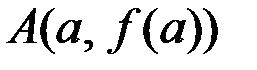 и
и 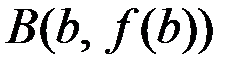 (см. Рис 3.2).
(см. Рис 3.2).
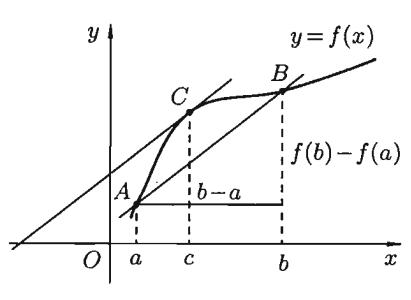
Рис 3.2
Следствие 3.1. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке.
Следствие 3.2. Если две функции имеют равные производные на некотором промежутке, то они отличаются на постоянное слагаемое.
Далее приводятся способы раскрытия неопределенностей вида 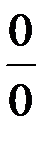 и
и 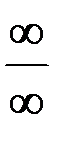 , которые основаны на применении производных.
, которые основаны на применении производных.
Теорема 3.4. (Правило Лопиталя раскрытия неопределенностей вида 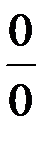 )
)
Пусть функции 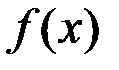 и
и 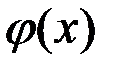 непрерывна и дифференцируемы в окрестности точки
непрерывна и дифференцируемы в окрестности точки 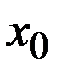 и обращаются на отрезке
и обращаются на отрезке 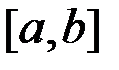 , дифференцируемы на интервале
, дифференцируемы на интервале 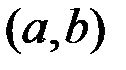 , пусть также
, пусть также 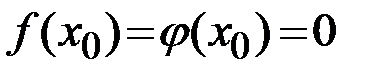 и
и 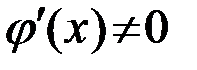 в окрестности точки
в окрестности точки 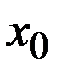 .
.
Если существует предел 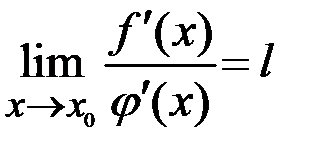 , то
, то 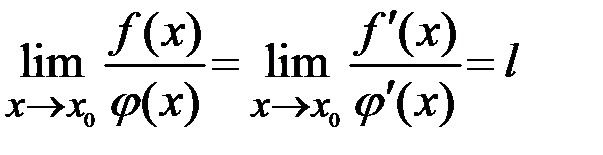 .
.
Теорема 3.5. (Правило Лопиталя раскрытия неопределенностей вида 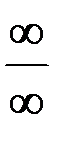 )
)
Пусть функции 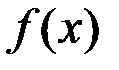 и
и 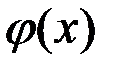 непрерывны и дифференцируемы в окрестности точки
непрерывны и дифференцируемы в окрестности точки 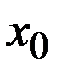 (кроме, может быть самой точки
(кроме, может быть самой точки 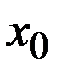 ), в этой окрестности
), в этой окрестности 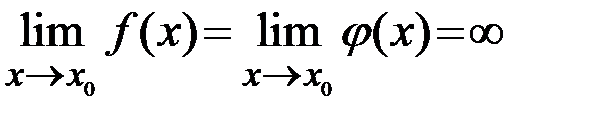 ,
, 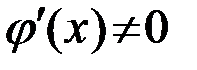 .
.
Если существует предел 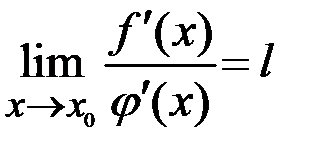 , то
, то 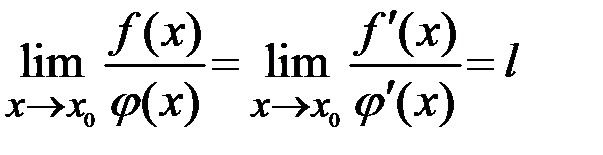 .
.
 2020-10-09
2020-10-09 147
147








