2014-02-02
718
Возможны различные подходы к определению эквивалентности. Неформально, две совокупности отношений эквиваленты, если они представляют одну и ту же информацию. Следовательно, точный смысл понятия эквивалентности зависит от определения информации, представляемой отношениями. В связи с этим выделим следующие два определения.
Определение ( эквивалентность по зависимостям). Две совокупности отношений представляют одну и ту же информацию, если они определены на одних и тех же атрибутах, и в них сохранены все зависимости данных (функциональные и многозначные). Это так называемая эквивалентность по зависимостям.
В этом определении под понятием " сохранены все зависимости данных " подразумевает следующее. Если исходной и результирующей схемами являются S0 SD, как это определено в предыдущем подразделе, тогда они эквивалентны по зависимостям, если:
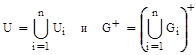
Таким образом, структура зависимостей отношения R порождается структурами зависимостей проекций Ri.
Определение (эквивалентность по данным). Две совокупности отношений представляют одну и ту же информацию, если эти совокупности отношений содержат одни и те же данные. В нашем случае при декомпозиции R на R1, R2,…, Rn исходное и результирующие отношения содержат одни и те же данные, если эта декомпозиция обладает свойством соединимости без потерь. Это так называемая эквивалентность по данным.
|
|
|
Разложение с сохранением данных. Существует следующее утверждение, которое дает условие сохранения зависимостей и данных при декомпозиции на два отношения.
Терема (о разложении с сохранением данных). Если R1(U1) R2(U2) являются результатом декомпозиции отношения R(U) с сохранением функциональных и/или многозначных зависимостей, то это разложение обеспечивает соединение без потерь тогда и только тогда, когда:
U1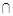 
U2 ® (или ®®) U1 – U2
либо
U1 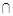U2 ® (или ®®) U2 – U1
Для разложений, состоящих более чем из двух отношений, можно использовать метод табло (он использует только функциональные зависимости). Пусть даны: множество функциональных зависимостей, исходное отношение и результирующие отношения. Процедура состоит в построении таблицы, строками которой являются разложенные отношения, а столбцами – список всех атрибутов (А1,..., An) эти отношений. Таблица заполняется символами aj, если элемент строки i и столбца j соответствует атрибуту Aj отношения Ri, в противном случае в таблице ставится bij. После заполнения таблицы следует итеративный просмотр всех функциональных зависимостей (X ® Y). если для атрибутов из Х найдутся строки, где в соответствующих местах стоят aj, то элементы bij этих строк, соответствующие столбцам атрибутов из Y, заменяются на aj. Если в результате появится строка таблицы, полностью заполненная aj, то данное соединение – без потерь; в противном случае это соединение с потерями.
|
|
|
| Пример. Пусть задано отношение R(A, B, C, D) и функциональные зависимости A ® C, D ® C, CD ® B, C ® D. Схема после разложения имеет вид: R1(A, B), R2(B, D), R3(A, B, C), R4(B, C, D). Исходная таблица выглядит так: Теперь примем во внимание функциональную зависимость A ® C. При этом получим следующее изменение в таблице: |
|
a1 a2 a3 b14
b21 a2 b23 a4
a1 a2 a3 b34
b41 a2 a3 a4
Далее, рассмотрим B ® C
a1 a2 a3 b14
b21 a2 a3 a4
a1 a2 a3 b34
b41 a2 a3 a4
Зависимость CD ® B ничего не дает. Далее, используем C ® D:
a1 a2 a3 a4
b21 a2 a3 a4
a1 a2 a3 a4
b41 a2 a3 a4
Имеется строка со всеми aj. Следовательно данное разложение без потерь.
Разложение с сохранением зависимостей. Свойство соединения без потерь не всегда гарантирует сохранение зависимостей. Аналогично, не каждое разложение, сохраняющее зависимости, обладает свойством соединения без потерь. Проиллюстрируем это на примерах.
Пример1. Рассмотрим отношение УЧЕБА (Студент, Предмет, Преподаватель), которое мы приводили при обсуждении BCNF. Это отношение имеет зависимости (Студент, Предмет) Преподаватель и Преподаватель Предмет.При разложении УЧЕБА на отношения ПРЕПОДАВАНИЕ(Студент, Преподаватель) и ДИСЦИПЛИНА(Преподаватель, Предмет).Потери будут отсутствовать, так как Преподаватель Предмет (см. теорему о разложении с сохранением данных), однако зависимость (Студент, Предмет) Преподаватель в разложении потеряна.
Пример2. Можно также привести следующий пример разбиения, сохраняющего зависимости, но не данные. Пусть в отношении R(A, B, C, D) имеется зависимость A ® B, тогда разбиение R1(A, B) и R2(C, D) эту единственную зависимость сохранит, но данные – нет (связь между всеми четырьмя атрибутами теряется).
Эквивалентность нормальных форм. Оказывается, что любая схема отношения может быть приведена в BCNF, таким образом, что декомпозиция обладала свойством соединения без потерь. Возможно также приведение в 3NF с получением декомпозиции, обладающей свойством соединения без потерь и сохраняющей зависимости. Однако схема отношения может оказаться не приводимой в BCNF с сохранением зависимостей. Например, отношение R(A, B, C) с функциональными зависимостями (A, B) ® C, C ® B, которое находится в 3NF, может быть приведено к нормальной форме Бойса-Кодда единственным образом: R1(A, C) и R2(B, C). Здесь эквивалентность по данным сохраняется, а эквивалентность по функциональным зависимостям – нет, так как зависимость (A, B) ® C теряется.
Таким образом, при использовании нормальных форм при проектировании следует помнить о следующем. Включая 3NF, преобразования можно производить с сохранением эквивалентности по зависимостям и по данным. Однако при получении нормальной формы Бойса-Кодда может теряться эквивалентность по функциональным зависимостям.
