Уравнения с разделяющимися переменными
Геометрический смысл дифференциального уравнения
Если функция f (x,y) определена в области DÍ R2 , то уравнение
y¢ = f (x, y) (7)
задает в любой точке области D значение углового коэффициента касательной к проходящему через эту точку графику решения уравнения (7).
Зададим в каждой точке (x,y)Î D направление касательной с помощью отрезка, тангенс угла наклона которого к оси Ox равен f (x, y). Построенное множество отрезков называется полем направлений уравнения (1).
Геометрически решить уравнение (7) означает, что требуется найти кривую y = j (x), которая в любой своей точке касается отрезка из поля направлений.
Тема 3: Интегрирование некоторых классов уравнений 1-го порядка.
Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
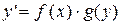 (1)
(1)
В дальнейшем будем предполагать, что функции 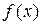 и
и 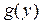 непрерывны в промежутках
непрерывны в промежутках 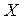 и
и 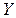 соответственно.
соответственно.
Заметим, что правая часть уравнения (1) равна произведению функции, зависящей только от 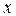 , на функцию, зависящую от
, на функцию, зависящую от 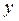 .
.
|
|
|
Теорема 1. В области, где 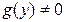 , общий интеграл уравнения (1) задается равенством
, общий интеграл уравнения (1) задается равенством
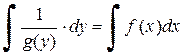 (2)
(2)
Замечание 1. Равенство (2) эквивалентно соотношению
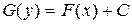 (3)
(3)
с произвольной константой 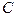 , где
, где 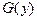 и
и 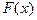 есть первообразные функций
есть первообразные функций 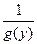 и
и 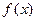 соответственно.
соответственно.
Замечание 2. Области где 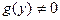 , есть прямоугольники (или в зависимости от
, есть прямоугольники (или в зависимости от 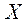 , полосы или полуполосы)
, полосы или полуполосы)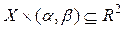 , где
, где 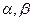 либо соседние нули функции
либо соседние нули функции 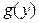 , либо граничные точки промежутка
, либо граничные точки промежутка 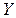 .
.
Из теоремы 1 следует такой план решения уравнения (1):
1) Решить алгебраическое уравнение
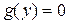 (4)
(4)
и получить частные решения уравнения (1)
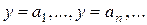 (5)
(5)
где 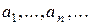 корни уравнения (4).
корни уравнения (4).
2) В областях, где 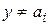 , уравнение (1) преобразовать так:
, уравнение (1) преобразовать так:
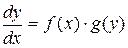 , ‘разделить’ переменные:
, ‘разделить’ переменные:
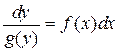 (6)
(6)
и получить общий интеграл (2), а затем (3).
3) Записать в ответ:
а) либо общее решение, полученное из равенства (3), либо общий интеграл (3);
б) особые решения из семейства (5) (не входящие в (3)).
Замечание. Равенство (6) нужно рассматривать как равенство дифференциалов с функцией 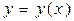 , являющейся решением уравнения (1).
, являющейся решением уравнения (1).
Пример 1. Решить уравнение
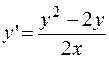 (7)
(7)
Это уравнение с разделяющимися переменными, где
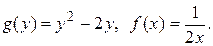
Решим уравнение (7) по плану.
1) Найдем корни 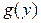 .
.
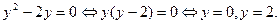
Следовательно, 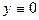 и
и 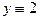 есть частные решения (7) при
есть частные решения (7) при 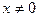 .
.
2) В области, где 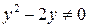 , разделим переменные:
, разделим переменные:
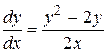 ;
; 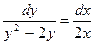 ;
;
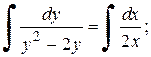 (8)
(8)
Найдем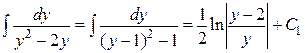 ;
;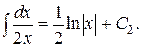 Поэтому из (8) получим,
Поэтому из (8) получим, 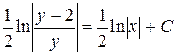 , где
, где 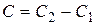 .
.
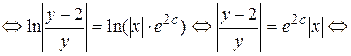
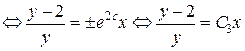 , где
, где 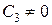 .
.
Выразим отсюда 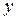 :
: 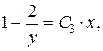
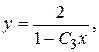 где
где 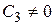 . (9)
. (9)
Заметим, что если положить 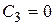 , то получим
, то получим 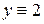 , что есть частное решение, полученное в пункте 1).
, что есть частное решение, полученное в пункте 1).
Заметим также, что частное решение 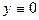 не входит в семейство (9) ни при каком
не входит в семейство (9) ни при каком 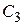 , то есть это особое решение.
, то есть это особое решение.
Ответ: 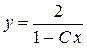 при
при 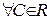 - общее решение,
- общее решение, 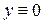 - особое решение.
- особое решение.
Пример 2. Решить уравнение с дифференциалами:
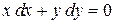 . (10)
. (10)
|
|
|
Здесь 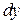 есть дифференциал неизвестной функции
есть дифференциал неизвестной функции 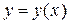 .
.
Разделив уравнение (10) на 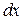 , получим дифференциальное уравнение
, получим дифференциальное уравнение
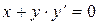 ,
,
которое можно разрешить относительно 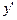 и дальше решать по плану. Однако можно этого не делать, поскольку в (10) переменные можно "разделить" сразу:
и дальше решать по плану. Однако можно этого не делать, поскольку в (10) переменные можно "разделить" сразу:
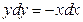 .
.
Интегрируя получим: 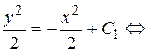
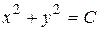 , где
, где 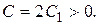
Это и есть общий интеграл уравнения (10), который задает семейство концентрических окружностей радиуса 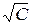 с центром в точке (0,0).
с центром в точке (0,0).
Замечание. Другие, рассмотренные ниже, типы дифференциальных уравнений с помощью подходящих подстановок сводятся к уравнениям с разделяющимися переменными.
Определение. Однородным дифференциальным уравнением первого порядка называется уравнение вида
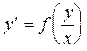 . (1)
. (1)
Пример. Уравнение
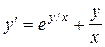 . (2)
. (2)
является однородным. Здесь 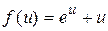 .
.
Однородное уравнение (1) сводится к уравнению с разделяющимися переменными. Для этого нужно ввести новую неизвестную функцию
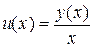
 2014-02-17
2014-02-17 794
794








