Рассмотрим систему материальных точек, массами m1,m2 и там далее, движущиеся со скоростями v1,v2, и так далее. Пусть F1,F2,…(штрих) – это равнодействующая действующих сил, а через f1,f2,…
Тогда
Mdv1/dt=F1(штрих)+F1+f1 m1(v1dv1)-(F|1+F1)*dr1 = f1df1
Mdv2/dt=F2(штрих)+F2+f2 *dri m2(v2dv2)-(F|1+F1)*dr2 = f1dr2
Mdvn/dt=Fn(штрих)+Fn+fn mn(vndvn)-(F|n+Fn)drn=fndrn
+
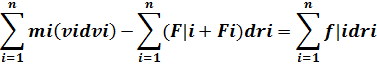
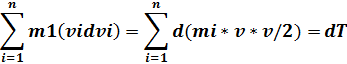
Таким образом
d(T+П)=dA
A12= 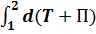
Если их консервативные силы = 0, то
d(T+П)=0
T+П=E=const
То есть полная механическая система остается постоянной. Закон сохранения механической энергии. В системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, то есть не изменяется с течением времени. Механические системы, на тела которых действуют толь консервативные силы, называют консервативными системами. Закон сохранения механической связан с однородностью времени. Однородность времени проявляется в том, что физические законы инвариантны, относительно выбора начала отсчета времени. Диссипативные системы - это системы, в которой механическая энергия уменьшается за счет преобразования других форм энергии.
|
|
|
Изучить самостоятельно:
· Графическое предстваление энергии
· Удар абсолютно упругих и не упругих тел
· Момент импукльса и закон его сохранения
При движении математической точки с течением времени ее координаты изменяются
В общем ее движение определяется скалярным уравнением
x=x(t), y=y(t), z=z(t) (1)
r=r(t) (2)
Уравнения 1 и 2 называются кинематическим уравнением движения математической точки
Число независимых координат определяющих положение математической точки в называется числом степеней свободы
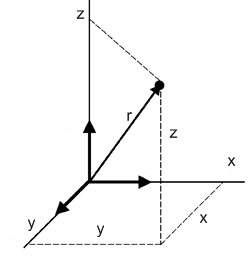
Траектория – это линия вдоль которой движется мат. точка
Траектория движения может быть прямолин или криволин
Путь – длина траектории, скаляр физ величина
Перемещения – это векторная физическая величина, направ. отр. прямой, соед. начальное и конечное положение тела
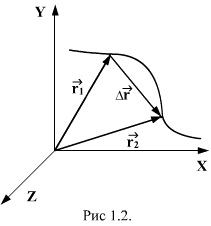
∆r=r2-r1 (вектор)
∆S- путь
Скорость
Для характеристики движения вводится векторная величина – скорость
Пусть мат. точки по какой-то криволин траектории, так что в нач момент времени ей соответствует радиус вектор R0. В течение малого промежутка времени ∆t, точка пройдет путь ∆S и получ. перемещение ∆r бесконеч. малым.
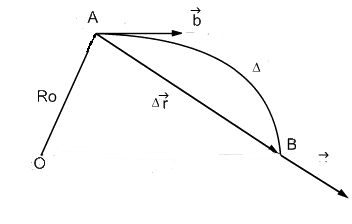
Вектор средней скорости называется отношением приращения ∆R рад вектора точки к промежутку времени ∆t

При ∆t стрем к 0, сред скорость стрем к пред знач, назыв мгновенной скоростью
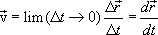
Мгновенная скорость равна первой производной радиус вектора по времени
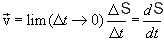
Динамика вращательного движения
Кинет. энерг. вращ. тела
Берем абсолют твердое тело, которое вращ вокруг неподвиж. оси и проход через него. Мысленно разбив это тело на элем объемы m1,m2,…mn, кот наход на расстоянии r1,r2,…,rn. Если тверд тело привести во вращ. вокруг оси, то эти элем объемы будут двигаться со скор v1,v2,…vn. Так как это абсолют твердое тело то его углов. скор. будет одинак. для всех элементар. объемов.
|
|
|
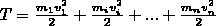
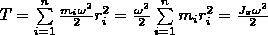
Кинет. энергия цилиндра, скатывающегося по наклонной поверхности
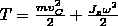
Момент силы
Уравнение динам. вращ. движ. тверд. тела
Моментом силы относит неподвижной т.О назыв физич величина, опред. вектор. произвед. радиус-вектора r силы F.
М = [rF]
M=F*r*sinα
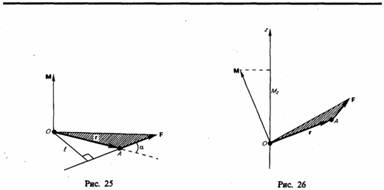
Момент силы относительно неподвиж оси Z назыв скалярная величина Mr равная проекции вектора момента силы на эту ось, определ, относительно произвольной т.О этой оси. Если ось Z совпадает с направлением вектора M то 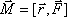 z
z
Получим выражение для работы при вращ абсолют. твердого тела
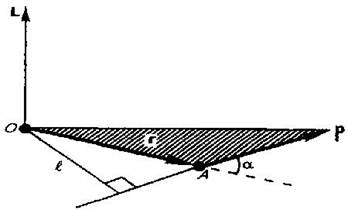
Точка B –точка приложения силы F, r – радиус вектор. При повороте тела на малый угол dS. точка проходит путь dS.
dS=r*d*φ
dA=F*sinα*r*d* φ=F*r*sinα*d* φ=Mz*d* φ
dA=dT
T=(Jz*ω^2)/2
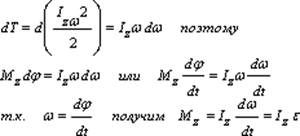
Если ось Z – проходит через центр масс то:
M=J*έ – уравн динам. вращ. движ. абсолют тверд тела
Момент силы относит. неподвижн. оси Z равен произв. относит. той же оси на углов. ускорение
Момент импульса. Закон его ускорения
Если проводить аналогию между поступат. и вращат. движением, то аналогией импульса тела при поступ движении является момент импульса при вращат движении.
Момент силы (кол-во движения) материал. точки А относительно неподвиж. т.О назыв вектор. велич. определяемая равенством:
L - момент импульса
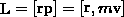
Модуль вектора момента импульса
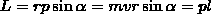
Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса ri со скоростью vi
Момент импульса относит. оси Z:
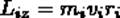
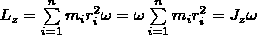
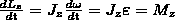
Первая произв. момента импульса твердого тела относительно оси равна мом. сил относит. той же оси
Имеет место векторное равенство если проход. через ось
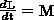
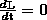

Данное выражение явл. законом сохранения момента импульса.
момент импульса замкнутой системы сохран.,то есть не изменяется с течением времени
Гармонический осциллятор.
Пружинный физический и математический маятники
Гармоническим осциллятором называется система, которая совершает колебания, описываемые выражением вида:
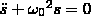
S=A*cos(ω0*t+φ)
Примерами гармон. осцил. явл. пружин.,физ. и математ. маятники.
Пружинный маятник
Это груз массой m, подвеш. на абсолютно упругой пружине и соверш. гармон. колеб. под действием упругой силы F
F=-k*x
Тогда по второму закону Ньютона:
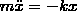
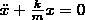
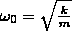
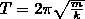
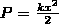
Физический маятник
Это твердое тело, соверш. колебания, под действием силы тяжести вокруг неподвиж. горизонт. оси, проходящей через т.О, не совпад. с центром масс тела.
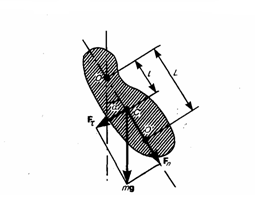
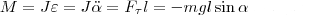
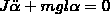
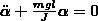
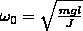
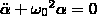
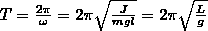
Точка О` располагающаяся на продолж Z называется центром качания физического маятника.
Математический маятник
Это идеализирована система, состоящая из MT массой m подвешенного на невесомой,нерастяжимой нити и колеблющийся под действием силы тяжести
Y=m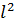
T=2π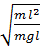 =2π
=2π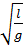
Математический маятник - частный случай физического
Приведенная длина физического маятника – это длина такого математического маятника, период колебания которого совпадает с периодом данного физического маятника
Дифф. уравнение свободных затухающих колебаний и его решение. Автоколебания
Рассмотрим свободные затухающие колебания – это колебания, амплитуда которых уменьшается с течением времени из-за потери энергии реальной колебательной системы.
Закон затухающих колебаний определяется св-вами колебательной сиcтемы. Обычно рассматриваются системы. Линейные системы- это идеализированные реальные системы в которых параметры, определяющие физ. св-ва системы в ходе процессы не изменяются
|
|
|
Линейными сист. например является пружинный маятник – при малых растяжениях пружины, колебательный контур – емкость, индуктивность, сопротивление которого не зависит от тока и напряжения в контуре.
Различные по своей природе системы описываются идентичными линейными дифференциальными уравнениями
Дифференциальное уравнение свободных затухающих колебаний системы задается в виде:
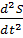 +2δ
+2δ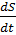 +
+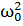 S=0
S=0
S=Acos(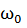 t+φ)
t+φ)
δ – коэффициент затухания(const), 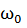 -циклическая частота свободных незатухающих колебаний той же колебательной системы и называется собственной частотой колебательной системы
-циклическая частота свободных незатухающих колебаний той же колебательной системы и называется собственной частотой колебательной системы
Рассмотрим решение уравнений
S=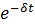 u
u
U=u(t)
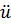 +(
+(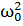 -
-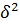 )u=0
)u=0
Решение этого уравнения зависит от знака коэффициента (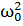 -
-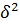 )
)
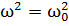 -
-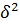 >0,тогда
>0,тогда 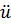 +
+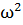 u
u
U=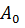 cos(⍵T+ϕ)
cos(⍵T+ϕ)
A=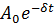 A-амплитуда затухающих колебаний
A-амплитуда затухающих колебаний
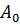 - начальное
- начальное
Промежуток времени τ=1/δ называется временем релаксации. Это время, в течение которого амплитуда затухающих колебаний уменьшится в е раз
Затухающие колебания не являются периодическими. Затухание мало, условно можно пользоваться понятием периода
T=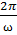
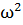 =
=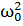 -
-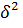
T=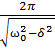
Если А(t)- амплитуда в момента времени t, A(T+t)- амплитуда в момент t через период, тогда имеет место соотношение:
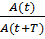 =
=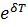
ϴ=ln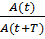 =ln
=ln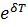 =δT=T/τ=1/
=δT=T/τ=1/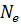
ϴ- логарифмический декремент затухания, 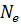 - число колебаний, происходящих в течение времени, за которое амплитуда уменьшается в е раз.
- число колебаний, происходящих в течение времени, за которое амплитуда уменьшается в е раз.
[ Q ]- добротность
Если лог. декремент затухающих колебаний, то
Q=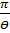 =π
=π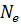 =
=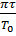 =
=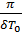 =
=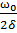
Данная формула справедлива когда 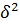 значительно меньше
значительно меньше 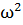
Свободные затухающие колебания пружинного маятника
Для пружинного маятника массы m совершается колебания под действием силы F=-kx, 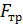 =-rʊ=-r
=-rʊ=-r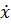
m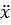 =-kx-r
=-kx-r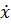
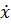 -первая производная,
-первая производная, 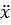 - вторая производная
- вторая производная
m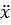 +r
+r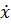 +kx=0
+kx=0
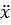 +
+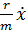 +
+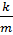 x=0
x=0
δ=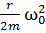 =
=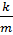
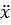 +2δ
+2δ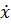 +
+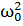 x=0 – дифференциальное уравнение затухающих колебаний пружинного маятника
x=0 – дифференциальное уравнение затухающих колебаний пружинного маятника
X=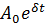 cos(⍵t+φ)
cos(⍵t+φ)
⍵=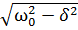 =
=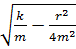
Q=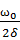 =
=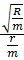 =
=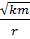
При увеличении коэффициента затухания δ период затухающих колебаний растет, при δ=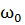 период стремится к бесконечности. В этом случае процесс не будет колебательным, он называется апериодическим.
период стремится к бесконечности. В этом случае процесс не будет колебательным, он называется апериодическим.
|
|
|
Автоколебания- это колебания, поддерживаемые в диссипативной системе за счет постоянного внешнего источника энергии, причем св-ва этих колебаний определяются самой системой.
Автоколебательная система сама управляет внешними воздействиями, обеспеч. согласов. поступления энергии определенными порциями в нужный момент времени.
Пример автоколебаний: часы, ход часов, ДВС, паровые турбины, ламповый генератор и т.д.
Дифф. уравнение вынужденных механических колебаний и его решение
В реальной колебательной системе постоянно происходит потеря энергии, если рассмотреть механические колебания, то потеря энергии компенсируется внешней вынужденной силой.
Эта сила: F=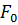 cos⍵t
cos⍵t
Для пружинного маятника:
m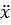 =-kx-r
=-kx-r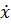 +
+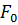 cos⍵t
cos⍵t
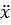 +2δ
+2δ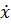 +
+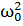 x=
x=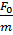 cos⍵t
cos⍵t
Колебания, возникающие под действием внешней переодически изменяющейся силы называются вынужденными механическими колебаниями
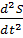 +2δ
+2δ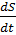 +
+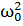 S=
S=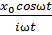 (1),
(1), 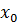 =
=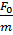
Решение уравнения (1) равно сумме общего решения однородного уравнения:
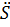 +2δ
+2δ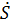 +
+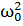 S=0 и частного решения неоднородного уравнения. Найдем частное решение:
S=0 и частного решения неоднородного уравнения. Найдем частное решение:
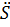 +2δ
+2δ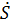 +
+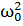 S=
S=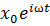 (*)
(*)
S=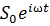
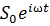 (-
(-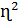 +2iδɳ+
+2iδɳ+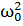 )=
)= 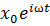 - справедливо в каждый момент времени
- справедливо в каждый момент времени
ɳ=⍵, тогда получим: 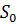 =
=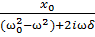 =
=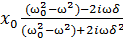
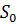 =A
=A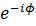
A=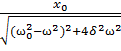 (2)
(2)
Φ=arctg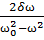 (3)
(3)
Решение уравнения имеет вид:
S=A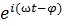
Частное решение неоднородного уравнения (1) имеет вид:
S=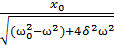 cos(⍵t-arctg
cos(⍵t-arctg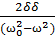 ) (4)
) (4)
Решение уравнения (1) равно сумме общих однородных решений уравн.
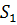 =
=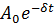 cos(
cos(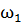 +ϕ) (5)
+ϕ) (5)
Слагаемое (5) играет существенную роль пока колебания не установлены, как только это произошло- то опред. уравнением (4).
Амплитуда и фаза вынужденных механических колебаний.
Рассмотрим зависимость амплитуды вынужденных колебаний от частоты ⍵. Рассматривая механические колебания в качестве колеблющейся величины, выбирают смещение х колеблющегося тела.
Из формулы для амплитуды(2) следует, что амплитуда смещения имеет максимум. Чтобы определить резонансную частоту(обозначается 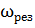 ) т.е. частоты при которой амплитуда смещения достигает максимума, нужно найти максимум функции, вычислить производную и приравнять к 0.
) т.е. частоты при которой амплитуда смещения достигает максимума, нужно найти максимум функции, вычислить производную и приравнять к 0.
-4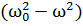 ⍵+8
⍵+8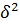 ⍵=0
⍵=0
⍵=0, 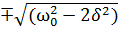 ,
,
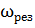 =
=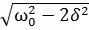
Явление резкого возрастания амплитуды вынужденных колебаний, при приближении частоты вынуждающей силы к частоте равной или близкой к собственной частоте колебательной системы, называется механическим резонансом
При 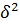 много меньше
много меньше 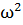
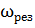 =
=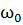
Если подставим в выражения для амплитуды:
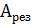 =
=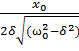
Представим резонансные кривые.
Если ⍵ -> 0, то А -> 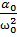
Эту велечину называют статическим отклонением
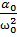 =
=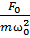
Если ⍵->∞, тогда все резонансные кривые асимпотически стремятся к 0
При малом затухании (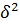 много меньше
много меньше 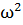 )
)
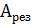 =
=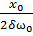 =
=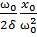 =Q
=Q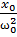
tgϕ=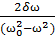 – следует, что фазы вынуждающей силы и собственных колебаний совпадают δ=0, во всех остальных случаях различные.
– следует, что фазы вынуждающей силы и собственных колебаний совпадают δ=0, во всех остальных случаях различные.
При ⍵=0, ϕ=0
При ⍵=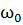 , φ=
, φ= не зависимо от коэффициента затухания когда ⍵->∞, ϕ->π.
не зависимо от коэффициента затухания когда ⍵->∞, ϕ->π.
Упругие волны
Продольные и поперечные волны.
Колебания, возбуждаемые в какой-либо точке среды распространяются в ней с какой то скоростью V, зависящей от свойства среды, передаваясь от одной точки к другой.
Процесс распространения колебаний в сплошной среде называется волновой процесс.
При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия.
Основным св-вом всех волн (независимо от их природы) является:
перенос энергии без переноса в-ва.
Типы волн:
· Волны на поверхности жидкости
· Упругие
· Электромагнитные волны
Упругими волнами называются механические возмущения в упругой среде.
Упругие волны бывают продольные и поперечные.
В поперечных волнах частицы среды колеблются в направлении перпендикулярном направлении распространения волны. (твердые тела)
 ↨ ↨
↨ ↨
Для продольных волн колебания частиц среды происходит в таком же направлении, в каком распространяется волна.(жидкости, газы, твердые тела)

Продольные волны могут возбуждаться в средах, в которых возникают упругие силы деформации сжатия и растяжения, т.е. в твёрдых, жидких и газообразных.
Поперечные волны возбуждаются в средах, в которых возникают упругие силы при деформации сдвига, т.е. в твёрдых телах.
Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармоническими.
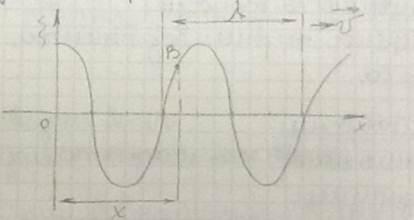
На рисунке представлена гармоническая поперечная волна, распространяющая в положительном направлении относительно оси Х со скоростью V.
Зависимость смещения оси частиц среды, участвующих в волновом процессе, от величины Х от источника О до … точке В в фиксированный момент времени.
График волны и колебаний похожи, но по существу они различаются: график волны показывает зависимость смещения всех частиц среды от … до источника колебаний в данный момент времени, а график колебаний - зависимость смещений данной частицы.
Расстояние между ближайшими точками, колеб. в одинаковой фазе, называется длинной волны.
λ=ʊT, T=1/ν
λ=ʊ/ν-> ʊ=λν
Геометрической место точек до которых доходит колебание к моменту времени t называется волновым фронтом.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. В каждый момент времени можно провести … множество волновых поверхностей, а волновой фронт только один.
Волновой фронт точки является волновой поверхностью.
Волновые поверхности могут представлять собой параллельных плоскостей или совокупности … сфер.
Бегущими волнами называются волны, которые переносят в пространстве энергию.
Перенос энергии характеризуется вектор. Плотности потока энергии (вектор Умова)
Вектор Умова совпадает с направлением переноса энергии, а по модулю он равен энергии переносимой волной за единицу времени через единичную площадку перпендикулярно направлению распространению волны.
Уравнение бегущей волны.
ξ-“Велечина кеи?”
ξ(0,t)=AcosωT
ζ=x/ʊ-промежуток времени отст. В
ξ(x,t)=Acos(t-x/ʊ) –ур. бегущей волны
ξ(x,t)=Acos(t+x/ʊ)- если волна распространяется противоположно оси х
В общем случае уравнение плоской волны распространяется в положительном направлении ох имеет вид.
ξ(x,t)=Acos[ω(t-x/ʊ)+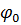 ]
]
A=const- амплитуда волны
⍵-циклическая частота
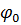 -шаг фазы волны
-шаг фазы волны
ω(t-x/ʊ)+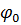 -фаза волны
-фаза волны
Волновое число
К=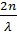 =
=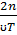 =
=
ξ(x,t)=Acos(⍵t-kx+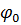 )
)
Уравнение для плоской волны через формулу Эйлера
⍵t-kx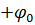 =const
=const
dt- dx=0
dx=0
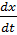 =ʊ
=ʊ
ʊ-фазовое ʊ
ξ(r,t)=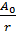 cos(
cos(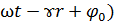
r- Расстояние от источника до рассматриваемой точки
Справедливо, если источник сферических волн, т.е. различных источников
ʊ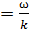
Если фазовая скорость волн в среде зависит от их частоты – дисперсия. Распространение волн в однородной изотропной среде описывается волновым уравнением: 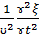
∆ξ=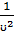 =
=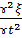
∆-оператор Лапласа
Решением уравнения является уравнение новой волны, плоской или сферической. Для плоской 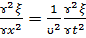
волны распространяется в направлении оси ОХ.
 2014-02-18
2014-02-18 1731
1731








