Описание ФАЛ в виде алгебраического выражения

Таблица истинности для трех переменных

Словесное описание ФАЛ

Проиллюстрируем словесное описание ФАЛ на примере.

Пример 1.5. Логическая функция трех переменных равна единице, если хотя бы две входные переменные равны единице (рис.1.1).

Данный вид описания наиболее часто применяется для первоначального, исходного описания поведения логического устройства.

Описание ФАЛ в виде таблицы истинности

Таблица, содержащая все возможные комбинации входных переменных х_{n- 1} ... х₁х_о и соответствующие им значения выходных переменных z _i; называется таблицей истинности или комбинационной таблицей. В общем случае таблица истинности содержит 2ⁿ строк и т + n столбцов. Существуют таблицы истинности переменных и функций.

Таблица истинности переменных

Проиллюстрируем построение таблицы истинности на примере.

Пример 1.6. Составить таблицу истинности (табл. 1.4) для ФАЛ из примера 1.5.

Р е ш е н и е. Данная таблица имеет по четыре столбца и строки.

Таблица 1.4

Таблица истинности функций

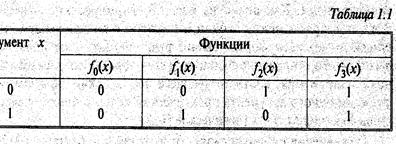Таблица истинности для функций одного аргумента представлена в табл.1.5

Аргумент x

Табл.1.5

Если число аргументов функции равно n, то число различных сочетаний (наборов) значений

_n

аргументов составляет 2ⁿ, а число различных функций и аргументов 2². Так, при n = 2 число наборов значений аргументов равно 2² = 4, число функций 2⁴ = 16. Таблица истинности функций двух аргументов представлена табл. 1.6.

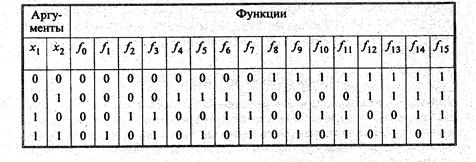
Табл. 1.6

В табл. 1.7 приведен перечень логических операций, используемых при записи логических выражений.

Таблица 1.7

Таблица логических операций

Обозначение логических операций	Таблица истинности	Как читается	Название операции
x 1
Основное	Дополни-тельные	x2
x1 x2	x1 x2 x1 Ù x2 x1 & x2	x1 · x2					x1 и x2	Конъюнкция; логическое И; логическое произведение
x1 Ú x2	x1 + x2	x1 Ú x2					x1 или x2	Дизъюнкция; логическое ИЛИ; логическаясумма
x1 ® x2	x1 É x2	x1 ® x2					если x1 ,то x2; x1 влечет x2; x1 имплицирует x2	Импликация
x1 ~ x2	x1 º x2 x1 «x2	x1 ~ x2					x1 эквивалентно x2	Эквивалентность; равнозначность
x1 Å x2	x1 É x2	x1 Å x2					либо x1, либо x2; x1 неэквива­лентно x2	Сумма по модулю; неравнозначность; исключающее ИЛИ
x1 r x2	x1 ® x2 x1 É x2	x1 r x2					x1 запрет по x2; x1, но не x2	Запрет; отрицание импликации
x1 ï x2	—	x1 ï x					x1 и x2 несовместны	Логическое И-НЕ; элемент (штрих) Шеффера; отрицание конъюнкции
x1 ¯ x2	—	x1 ¯ x2					ни x1, ни x2	Логическое ИЛИ-НЕ; стрелка Пирса; функция Вебба; отрицание дизъюнкции
х	ù х	х			не х	Логическое НЕ; инверсия; логическое отрицание
х

Таблицы истинности дают полную информацию об устройстве и широко используются для их описания. Для этого входные переменные располагают в таблице истинности так, что их последовательность образует двоичное число x₁x₀ ,соответствующееномерунабора i в десятичной системе счисления (поэтому колонку с номерами наборов часто в таблицу не включают).

Составим таблицу (табл.1.8) полного набора логических функций для устройства с двумя входами и 16-ю выходами. Каждая функция Y_n является результатом выполнения одной из 16-ти операций над входными переменными x₁ и x₀ на всех i –ых наборах.

Таблица 1.8

Табл. истинности		Название операции (функции)
i	0	1	2	3	Запись операции (функции)
x1	0	0	1	1
x0	0	1	0	1
yo	0	0	0	0	0	Постоянный 0
Y1	0	0	0	1	x1· x0	Конъюнкция (И)
Y2	0	0	1	0	x1 ® x0 = x1 x0	Запрет по x0
Y3	0	0	1	1	x1	Переменная x1
Y4	0	1	0	0	x0 ® x1 = x1 x0	Запрет по x1
Y5	0	1	0	1	x0	Переменная x0
Y6	0	1	1	0	x1 Å x0 = x1 x0 + x1 x0	Неравнозначность
Y7	0	1	1	1	x1 + x0	Дизъюнкция (ИЛИ)
Y8	1	0	0	0	x1 ¯ x2 = x1 + x0	Стрелка Пирса (ИЛИ-НЕ)
Y9	1	0	0	1	x1 ~ x0 = x1 x0 + x1 x0	Равнозначность
Y10	1	0	1	0	x0	Инверсия (НЕ) x0
Y11	1	0	1	1	x0 ® x1 = x1 + x0	Импликация от x0 к x1
Y12	1	1	0	0	x1	Инверсия (НЕ) x1
Y13	1	1	0	1	x1 ® x0 = x1 + x0	Импликация от x1 к x0
Y14	1	1	1	0	x1 ï x0 = x1 x0	Штрих Шеффера (И-НЕ)
Y15	1	1	1	1	1	Постоянная 1

Возможен и аналитический способ записи логической функции. В обычной математике аналитический способ представления функции предполагает запись функции в виде математического выражения, в котором аргументы функции связываются определенными математическими операциями. Подобно этому аналитический способ задания логической функции предусматривает запись функции в форме логического выражения, показывающего, какие и в какой последовательности должны выполняться логические операции над аргументами функции.

Функции одного аргумента (табл. 1.5) представляются следующими выражениями:

f₀ (х) = 0 (константа 0), f ₁ (х) = х,

f₂ (х) = х, f₃ (х) = 1 (константа 1).

Устройства, реализующие функции f₀ (х), f₁ (х) и f₃ (х), оказываются тривиальными. Как видно из рис. 1.1, формирование функции f₀ (х) требует разрыва между входом и выходом с подключением выхода к общей точке схемы, формирование функции f₁ (х) — соединения входа с выходом, формирование функции f₃ (х) — подключения выхода к источнику напряжения, соответствующего лог.1. Таким образом, из всех функций одного аргумента практический интерес может представлять лишь функция f₂ (х) = х (логическое НЕ).

Из сравнения таблиц истинности функций f₀ (х),... f₁₅ (х) (табл. 1.6) с таблицами истинности логических операций (табл. 1.7) следует:

x f₀ (x) x f₁ (x) f₃ (x)

+

-

Рис. 1.1

При описании ФАЛ алгебраическим выражением используются две стандартные формы ее представления.

Дизъюнктивной нормальной формой (ДНФ) называется логическая сумма элементарных логических произведений, в каждое из которых аргумент или его инверсия входит один раз.

Получена ДНФ может быть из таблицы истинности с использованием следующего алгоритма:

а) для каждого набора переменных, на котором ФАЛ равна единице, записывают элементарные логические произведения входных переменных, причем переменные, равные нулю, записывают с инверсией. Полученные произведения называют конституентами единицы;

б) логически суммируют все конституенты единицы.

Пример 1.7. Запись ДНФ для ФАЛ, заданной в примере 1.6.

Р е ш е н и е. Согласно приведенному алгоритму из табл. 1.4 получим:

y (x₂, x₁, x₀) = x₂ x₁ x₀ + x₂ x₁ x_{0 +} x₂ x₁ x_{0 +} x₂ x₁ x₀

Дизъюнктивную нормальную форму, полученную суммированием конституент единицы, называют совершенной (СДНФ).

Конъюнктивной нормальной формой (КНФ) называется логическое произведение элементарных логических сумм, в каждую из которых аргумент или его инверсия входят один раз.

Получена КНФ может быть из таблицы истинности с использованием следующего алгоритма:

а) для каждого набора переменных, на котором ФАЛ равна нулю, записывают элементарные логические суммы входных переменных, причем переменные, значения которых равны единице, записывают с инверсией. Полученные суммы называют конституентами нуля;

б) логически перемножают все полученные конституенты нуля.

Пример 1.8. Запись КНФ для ФАЛ, заданной в примере 1.6.

Р е ш е н и е. Применяя вышеприведенный алгоритм к табл. 1.4, получаем.

y (x₂, x₁, x₀) = (x_{2 +} x_{1 +} x₀)(x_{2 +} x_{1 +} x₀ )(x_{2 +} x_{1 +} x₀)(x_{2 +} x_{1 +} x₀)

Конъюнктивную нормальную форму, полученную суммированием конституент нуля, также называют совершенной (СКНФ).

Рассмотренные методики позволяют получить математическую форму записи для самой функции. Иногда удобнее применять не саму ФАЛ, а ее инверсию. В этом случае при использовании вышеописанных методик для записи СДНФ необходимо выбирать нулевые, а для записи СКНФ — единичные значения функции.

Пример 1.9. Для ФАЛ из примера 1.6 записать СДНФ и СКНФ инверсной функции.

Р е ш е н и е. Воспользовавшись табл. 1.4, запишем:

СДНФ: y (x₂, x₁, x₀) = x₂ x₁ x₀ + x₂ x₁ x_{0 +} x₂ x₁ x_{0 +} x₂ x₁ x₀

СКНФ: y (x₂, x₁, x₀) = (x_{2 +} x_{1 +} x₀)(x_{2 +} x_{1 +} x₀ )(x_{2 +} x_{1 +} x₀)(x_{2 +} x_{1 +} x₀)