Классы точности средств измерения.
Класс точности (КТ) — это обобщенная характеристика средства измерений, выражаемая пределами его допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.
Возможно несколько случаев обозначения класса точности:
1. Если, к примеру, у прибора 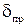 = 1,5 %, то в этом случае КТ на передней панели прибора обозначается 1.5 Если при этом
= 1,5 %, то в этом случае КТ на передней панели прибора обозначается 1.5 Если при этом 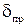 определяется по длине шкалы L (мм), то КТ обозначается в виде
определяется по длине шкалы L (мм), то КТ обозначается в виде
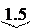
2. Если функция преобразования линейная, т. е. 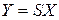 , то как известно, относительная погрешность измерения
, то как известно, относительная погрешность измерения
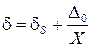 , (2)
, (2)
а
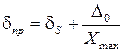 (3)
(3)
 Если при этом в (3) можно пренебречь вторым слагаемым, то например при
Если при этом в (3) можно пренебречь вторым слагаемым, то например при 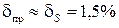 , КТ изображается в виде 1.5 В данном случае КТ по сути определяется погрешностью чувствительности прибора.
, КТ изображается в виде 1.5 В данном случае КТ по сути определяется погрешностью чувствительности прибора.
3. Если в (2) пренебречь слагаемым 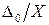 нельзя, то эту формулу можно представить как
нельзя, то эту формулу можно представить как
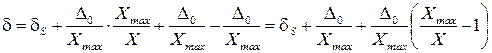
или окончательно в виде
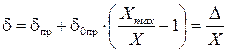 , (4)
, (4)
где 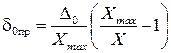 , по сути есть аддитивная приведенная погрешность. Очевидно, что
, по сути есть аддитивная приведенная погрешность. Очевидно, что 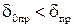 . В этом случае КТ может обозначаться в виде двух чисел
. В этом случае КТ может обозначаться в виде двух чисел 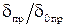 . Например:
. Например: 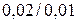 .
.
|
|
|
Важно отметить, что такое представление класса точности в виде двух чисел, обозначающих общую и аддитивную приведенную погрешности, позволяет оценить точность (относительную погрешность 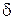 ) конкретного измерения величины
) конкретного измерения величины 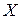 с помощью формулы (4) — в отличие от случаев 1 и 2, когда класс точности обозначает лишь минимальное значение
с помощью формулы (4) — в отличие от случаев 1 и 2, когда класс точности обозначает лишь минимальное значение 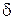 (при
(при 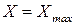 ).
).
4. В более сложных случаях КТ может выражаться буквами (A, B, C, D, …) или цифрами (I, II, III, IV). При этом классы, обозначаемые “A” или “I“ соответствуют наиболее точным приборам.
На практике чаще систематическая погрешность вносит больший вклад в погрешность измерения. Однако, рассмотрение вероятностных характеристик начнем со случайных погрешностей (СП)
В полученном результате измерения
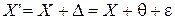 (5)
(5)
СП 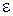 есть центрированная случайная величина. Это означает, что математическое ожидание случайной погрешности по определению равно 0:
есть центрированная случайная величина. Это означает, что математическое ожидание случайной погрешности по определению равно 0:
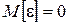 (6)
(6)
Следовательно, результат измерения физической величины, содержащий СП, так же представляет собой случайную величину с математическим ожиданием равным
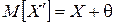 (7)
(7)
Наиболее полной характеристикой непрерывных случайных величин 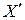 и
и 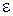 является их функция распределения и плотность распределения:
является их функция распределения и плотность распределения:
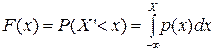 (8)
(8)
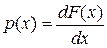 (9)
(9)
Функция 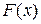 случайной величины
случайной величины 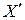 определяет вероятность
определяет вероятность 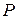 того, что значения этой величины меньше некоторого значения x. Очевидно, что при изменении x от
того, что значения этой величины меньше некоторого значения x. Очевидно, что при изменении x от 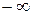 до
до 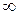 функция
функция 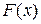 монотонно возрастает от 0 до 1. Следовательно, общая площадь под кривой
монотонно возрастает от 0 до 1. Следовательно, общая площадь под кривой 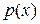 всегда равна 1:
всегда равна 1:
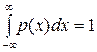 (10)
(10)
Плотности распределения 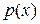 характеризует относительную вероятность того, что случайная величина
характеризует относительную вероятность того, что случайная величина 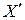 примет значение x. Поскольку формально непрерывная величина
примет значение x. Поскольку формально непрерывная величина 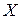 имеет на любом ограниченном интервале бесконечное множество значений
имеет на любом ограниченном интервале бесконечное множество значений 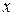 , то вероятность
, то вероятность 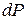 каждого из них бесконечно мала. Поэтому, чтобы иметь конечное значение,
каждого из них бесконечно мала. Поэтому, чтобы иметь конечное значение, 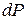 отнесена к бесконечно малому отрезку
отнесена к бесконечно малому отрезку 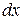 (см (8))
(см (8))
|
|
|
Для непрерывной случайной величины 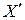 математическое ожидание
математическое ожидание
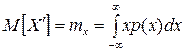 (11)
(11)
характеризует среднее значение этой величины. Из (7) следует, что разность между 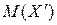 и истинным значением
и истинным значением 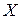 измеряемой величины представляет собой систематическую погрешность
измеряемой величины представляет собой систематическую погрешность 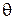 . В случае если
. В случае если 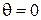 ,
, 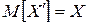 . Важно отметить, что поскольку случайный характер результата измерения
. Важно отметить, что поскольку случайный характер результата измерения 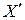 определяется наличием случайной погрешности
определяется наличием случайной погрешности 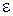 , кривая плотности распределения
, кривая плотности распределения 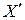 повторяет аналогичную кривую для
повторяет аналогичную кривую для 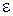 , со смещением на величину
, со смещением на величину 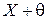 (рис. 2). В дальнейшем область значений
(рис. 2). В дальнейшем область значений 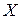 , в которой находится СП будем обозначать
, в которой находится СП будем обозначать 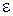 , т. е.
, т. е. 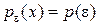 .
.
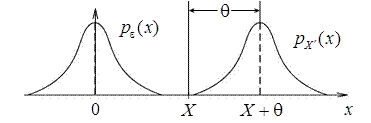
Рис. 2
Дисперсия
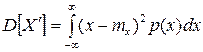 (12)
(12)
как известно количественно характеризует разброс значений случайной величины около ее математического ожидания. При этом
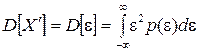 (13)
(13)
Неудобство использования дисперсии заключается в том, что ее размерностью является квадрат размерности измеряемой случайной величины. На практике удобнее использовать среднее квадратическое отклонение (СКО): 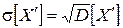 По существу СКО является среднеквадратической величиной случайной погрешности, т. е.
По существу СКО является среднеквадратической величиной случайной погрешности, т. е. 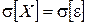 . Эту величину называют точечной оценкой СП.
. Эту величину называют точечной оценкой СП.
На практике кроме СКО бывает важно знать интервальную оценку СП, т. е. граничные значения 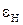 ,
,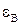 доверительного интервала
доверительного интервала 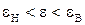 , в пределах которого находятся погрешности
, в пределах которого находятся погрешности 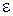 с достаточно высокой доверительной вероятностью
с достаточно высокой доверительной вероятностью 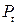 .
.
Взаимосвязь граничных значений, с доверительной вероятностью определяется соотношением:
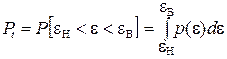 (14)
(14)
Если функция 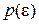 является четной, то
является четной, то 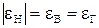 , то (14) примет вид:
, то (14) примет вид:
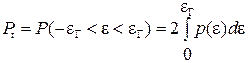 , (15)
, (15)
Чем выше вероятность Pt, тем шире доверительный интервал. Чем больше СКО 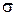 , тем больше
, тем больше 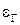 . При этом
. При этом 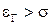 , т. е.
, т. е.
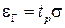 , (16)
, (16)
где коэффициент 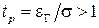 представляет собой нормированное граничное значение.
представляет собой нормированное граничное значение.
 2014-02-18
2014-02-18 681
681








