И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ

НЕКОТОРЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

СЛУЧАЙНОЙ ВЕЛИЧИНЫ

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ НЕПРЕРЫВНОЙ

Для непрерывных случайных величин математическое ожидание и дисперсия определяются так:

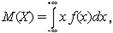
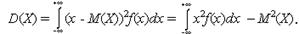
Все рассуждения, приведенные для математического ожидания и дисперсии дискретных случайных величин, верны и для непрерывных случайных величин.

■ Биномиальное распределение (распределение Бернулли) – распределение вероятностей случайной величины X с целочисленными значениями m = 0, 1,…, n, заданное формулой P_n(k) = P(X=m) = С_n^k·p^k·q^n-k = С_n^k·p^k·(1-p)^n-k, где n³1 и 0£p£1 – параметры, а С_n^k – биномиальный коэффициент. Биномиальное распределение– одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний; это – распределение вероятностей числа наступлений некоторого события («удачи») в n повторных независимых испытаниях, если при каждом испытании вероятность наступления этого события равна p.

▲ Теорема 2.29. Для биномиального распределения математическое ожидание M (X) = np, и дисперсия D (X) = np (1- p).

На практике для вычисления вероятностей P_n (k) при небольших n пользуются таблицами, а при больших n – приближенными формулами, основанными на предельных теоремах (Теорема Лапласа).

Пример 2.28. Определите математическое ожидание, дисперсию и стандартное отклонение случайной величины X, представляющей собой число положительных ответов в серии из 10 вопросов при вероятности положительного ответа p = 0,5 (см. пример 2.24).

Решение. Данная случайная величина имеет биномиальное распределение. По теореме 2.29 имеем: M (X) = np = 10·0,5 = 5; и D (X)= np (1- p) = 10·0,5·0,5 = 2,5; s=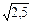» 1,581.

Ответ: 5; 2,5;» 1,581.

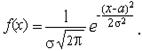■ Нормальное (Гауссово) распределение – распределение вероятностей непрерывной случайной величины, плотность вероятности которой задается функцией

(2.2)

Нормальное распределение играет особую роль в теории вероятностей и ее приложениях. Это наиболее часто встречающийся на практике закон распределения.При n ® ¥ биномиальное распределение приближается к нормальному (см. теорему Лапласа).

▲ Теорема 2.30. Функция распределения нормально распределенной случайной величины X задается формулой

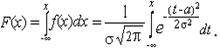▲ Теорема 2.31. Для нормального распределения математическое ожидание M (X)= a, дисперсия D (X) = s² и стандартное отклонение равно s.

Графики плотности вероятности и функции распределения нормального распределения показаны на рис. 2.7. График плотности вероятности нормального распределения показывает, что для нормально распределенной случайной величины вероятность отклонения от среднего значения быстро уменьшается с ростом величины отклонения.

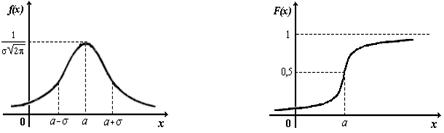Рис. 2.7

Формула (2.2) описывает целое семейство нормальных кривых, зависящих от двух параметров - a и s, которые могут принимать любые значения, поэтому возможно бесконечно много нормально распределенных совокупностей (каждую из них иногда обозначают N (a, s). Чтобы избежать неудобств, связанных с расчетами для каждого конкретного случая по достаточно сложной формуле (2.2), используют так называемое нормированное (или стандартное) нормальное распределение, для которого составлены таблицы. Нормированное нормальное распределение имеет параметры a = 0 и s = 1, т.е. распределение N (0,1). Его плотность вероятности и функция распределения задаются формулами

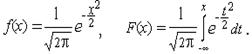
Эти функции табулированы. Пользуясь таблицами надо быть внимательным, т.к. часто через F (x) обозначают (и задают таблицы для этой функции) интеграл, у которого нижний предел равен – x или 0 (Функция Ф(x)). В силу четности функции f (x) достаточно задавать значения F (x) и Ф(x) только для положительных x. Все три функции связаны простыми соотношениями, позволяющими по любой из них вычислить значения для других: P (- x < X < x) = 2Ф(x); P (X < x) = 0,5+Ф(x); P (X > x) = 0,5 - Ф(x).

Для распределения N (a, s) вероятность попадания в промежуток с концами α и β (неважно, открытый или замкнутый) может быть выражена через Ф(x), т.е. вычислена с помощью таблиц:

P (α < X < β) = 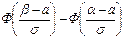. (2.3)

Вероятность того, что отклонение случайной величины X по абсолютной величине меньше заданного положительного числа d

P (| X – a | <d) = 2Ф(d/s). (2.4)

Пример 2.29. Количество баллов, полученных испытуемым, представляет собой нормально распределенную случайную величину с математическим ожиданием 40 баллов и средним квадратическим отклонением 3 балла. Найти: а) вероятность того, что количество набранных баллов произвольно взятого испытуемого не больше 43 баллов и не меньше 34 баллов; б) вероятность того, что количество набранных баллов отклонится от его математического ожидания не более чем на 1,5 балла.

Решение. Пусть X – количество баллов, полученных испытуемым. По условию a =40, α=34, β=43, s = 3. Тогда

а) P (34< X <43) =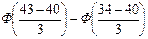= Ф(1) – Ф(-2)»Ф(1) + Ф(2) = 0,3413+0,4772 = 0,8185.

б) P (| X – 40| <1,5) = 2Ф(1,5/3) =2Ф(0,5)» 2·0,1915 = 0,383.

Ответ: а) 0,8185; б) 0,383.

Правило трех сигм. Вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973, т.е. P (| X – a | <3s) = 2Ф(3s/s) = 2·Ф(3)» 0,9973. Другими словами, в вероятностью 0,9973 (практически с единичной) нормально распределенная случайная величина окажется в пределах ±3s от среднего значения a, т.е. отклонения от среднего больше ±3s можно ожидать примерно в 1 случае из 370 испытаний.

В таблице 2.1 приведены полученные по формуле (2.4) вероятности того, что нормально распределенная случайная величина отклонится от своего среднего значения не более, чем на ±0,5s, ±s, ±2s, ±3s.

Таблица 2.1

Границы интервала, a ± x	a ± 0,5s	a ± s	a ± 2s	a ± 3s
Вероятность попадания в интервал	0,3829	0,6827	0,9545	0,9973

Пример 2.30. В некоторых международных играх по разным видам спорта должны участвовать N = 600 спортсменов. Известно, что размеры одежды V участников игр от 40-го (у гимнасток) до 62-го (у тяжелоатлетов). Оргкомитет игр решил подарить участникам майки с эмблемой игр. Швейной фабрике был сделан заказ на пошив маек свободного покроя трех условных размеров: I, II и III.Какие стандартные размеры (от 40-го до 62-го) разумно объединить в условные размеры I, II и IIIи сколько маек каждого из этих трех размеров следует сшить?

Решение. Считая, что размеры одежды V спортсменов имеют нормальное распределение, найдем среднее значение совокупности размеров (см. рис. 2.8):

` V = 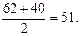Согласно правилу трех сигм считаем, что практически вся совокупность маек от 40-го до 62-го размеров попадет в интервал длиной 6s. При этом в центральную часть распределения (см. рис. 2.8) попадают размеры 48, 50, 52 и 54, им разумно присвоить условный размер II.На эти размеры всей совокупности будет приходиться примерно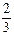маек, т. е. 600·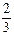= 400 маек.

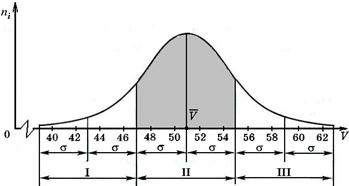
Рис. 2.8

В I условный размер войдут 40, 42, 44 и 46-й размеры, в III — 56, 58, 60 и 62-й размеры. Очевидно, на каждый из I и III условных размеров приходится 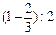= 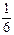от всей совокупности маек, т.е. по 600·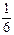= 100 маек.