Остовные деревья минимальной стоимости

Алгоритм построения минимального остовного дерева

Пусть даны n контактов на печатной плате, которые мы хотим электрически со-
единить. Для этого достаточно использовать n - 1 проводов, каждый из которых
соединяет два контакта. При этом мы обычно стремимся сделать суммарную
длину проводов как можно меньше.

Упрощая ситуацию, можно сформулировать задачу так. Пусть имеется связ-
ный неориентированный граф G = (V, Е), в котором V - множество контактов,
а Е множество их возможных попарных соединений. Для каждого ребра гра-
фа (и, v) задан неотрицательный вес w (и, v)(длина провода, необходимого для
соединения и и v). Задача состоит в нахождении подмножества Т 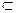Е, связы-
вающего все вершины, для которого суммарный вес

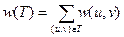
минимален. Такое подмножество Т можно считать деревом (в любом цикле один
из проводов можно удалить, не нарушая связности). Связный подграф графа G,
являющийся деревом и содержащий все его вершины, называют покрывающим
деревом (spanning tree) этого графа. (Иногда используют термин «остовное
дерево», или, короче, «остов».)

В этом разделе мы рассматриваем задачу о минимальном покрывающем дереве
(minimum-spanning-tree problem). Здесь слово «минимальное» означает «имеющее
минимально возможный вес». (Заметим в скобках, что если мы рассматриваем
только деревья, то условие неотрицательности весов можно отбросить, посколь-
ку во всех покрывающих деревьях одинаковое число рёбер и все веса можно
изменить на одну и ту же константу, сделав их положительными.) На рисунке 5.6 приведён пример связного графа и его минимального
остова.

Возвращаясь кпримеру с проводниками на печатной плате, объясним, по-
чему задача о минимальном дереве является упрощением реальной ситуации.
В самом деле, если соединяемые контакты находятся в вершинах единичного
квадрата, разрешается соединять его любые вершины и вес соединения равен
его длине, то минимальное покрывающее дерево будет состоять из трёх сторон
квадрата. Между тем все его четыре вершины можно электрически соединить
двумя пересекающимися диагоналями (суммарная длина 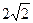< 3) и это ещё не предел (можно ввести две промежуточные точки, в которых проводники
сходятся под углом 120⁰).

В этом разделе мы рассмотрим два способа решения задачи о минимальном
покрывающем дереве: алгоритмы Крускала и Прима. Каждый их них легко
реализовать с временем работы O (Е × log V), используя обычные двоичные ку-
чи. Применив фибоначчиевы кучи, можно сократить время работы алгоритма
Прима до O (E + V × log V)(выигрыш существен, если | V | много меньше | Е |).

Оба алгоритма (Крускала и Прима) следуют «жадной» стратегии: на каждом
шаге выбирается «локально наилучший» вариант. Не для всех задач такой выбор
приведёт к оптимальному решению, но для задачи о покрывающем дереве это
так.

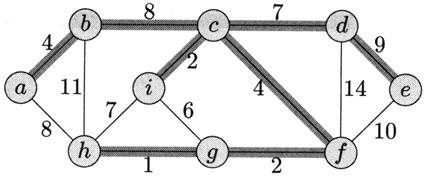
Рисунок 5.6 – Связный граф и его минимальный остов

На рис. 5.6 изображено минимальное покрывающее дерево. На каждом ребре графа указан вес. Выделены рёбра минимального покрывающего дерева (суммарный вес 37). Такое
дерево не единственно: заменяя ребро (b, c) ребром (а, h), получаем другое дерево того же
веса 37.