Алгоритм Прима

Как и алгоритм Крускала, алгоритм Прима следует общей схеме алгорит-
ма построения минимального остова. Он похож на алгоритм
Дейкстры поиска кратчайшего пути в графе. В алгоритме Прима
растущая часть остова представляет собой дерево (множество рёбер которого
есть А). Как показано на рис. 5.10, формирование дерева начинается с произ-
вольной корневой вершины r. На каждом шаге добавляется ребро наименьшего
веса среди рёбер, соединяющих вершины этого дерева с вершинами не из дерева.
По следствию 5.9 добавляемые рёбра являются безопасными для А, так что
в результате получается минимальный остов.

При реализации важно быстро выбирать лёгкое ребро. Алгоритм получает
на вход связный граф G и корень r минимального покрывающего дерева. В
ходе алгоритма все вершины, ещё не попавшие в дерево, хранятся в очереди
с приоритетами. Приоритет вершины v определяется значением key [ v ], которое
равно минимальному весу рёбер, соединяющих v с вершинами дерева А. (Если
таких рёбер нет, полагаем key [ v ] = 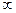.) Поле 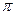[ v ] для вершин дерева указывает
на родителя, а для вершины v 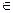Q указывает на вершину дерева, в которую
ведёт ребро веса key [ v ] (одно из таких рёбер, если их несколько). Мы не храним
множество А рёбер строящегося дерева явно; его можно восстановить как

А = {(v, 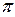[ v ]): v 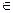V\ { r } \ Q }.

В конце работы алгоритма очередь Q пуста, и множество

А = {(v, 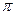[ v ]): v 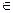V\ { r }}

есть множество рёбер покрывающего дерева.

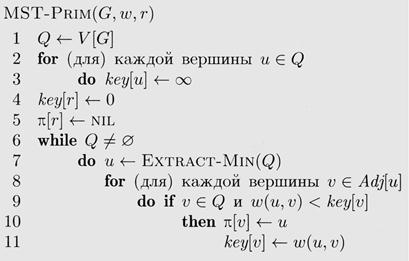
Листинг 5.10 – Алгоритм Прима

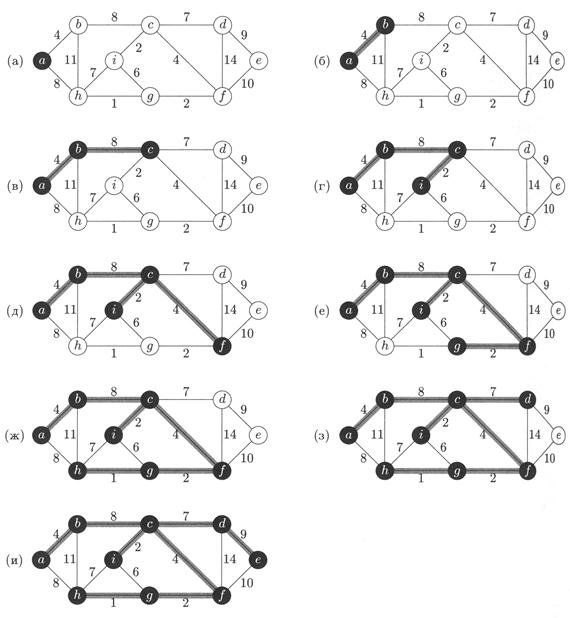
Рисунок 5.10 – Работа алгоритма Прима

На рис. 5.10 показана работа алгоритма Прима. Рёбра, входящие в дерево А. выделены серым: вершины дерева – чёрным На каждом
шаге к А добавляется лёгкое ребро, пересекающее разрез между деревом и его дополнением.
Например, на втором шаге можно было бы добавить любое из рёбер (b. с)и (a, h). После исполнения строк
1 – 5 и первого прохода цикла в строках 6 – 11 дерево состоит из единственной
вершины r, все остальные вершины находятся в очереди, и значение key [ v ] для
них равно длине ребра из r в v или 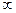, если такого ребра нет (в первом случае 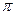[ v ] = r). Таким образом, выполнен описанный выше инвариант (дерево есть
часть некоторого остова, для вершин дерева поле 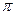указывает на родителя,
а для остальных вершин на «ближайшую» вершину дерева – вес ребра до неё
хранится в key [ v ]. Этот инвариант выполняется и после следующих итераций
цикла.

Время работы алгоритма Прима зависит от того, как реализована оче-
редь Q. Если использовать двоичную кучу, инициализацию в строках
1 – 4 можно выполнить с помощью процедуры BUILD-HEAP за время O (V). Далее
цикл выполняется | V | раз, и каждая операция EXTRACT-MIN занимает время
O (log V), всего O (V × lоg V). Цикл for в строках 8 – 11 выполняется в общей слож-
ности O (E)раз, поскольку сумма степеней вершин графа равна 2×| Е |. Проверку
принадлежности в строке 9 внутри цикла for можно реализовать за время O (1),
если хранить состояние очереди ещё и как битовый вектор размера | V |. При-
сваивание в строке 11 подразумевает выполнение операции уменьшения ключа
(DECREASE-KEY)) которая для двоичной кучи может быть выполнена за вре-
мя O (log V). Таким образом, всего получаем O (V × log V + E × log V) = O (E × log V) –
та же самая оценка, что была для алгоритма Крускала.