Векторное произведение векторов

Три вектора называются упорядоченной тройкой, если указано, какой из этих векторов является первым, какой – вторым, какой – третьим.

Рассмотрим ортонормированные базисы, приведенные к общему началу. Тогда возникает вопрос: можно ли все эти базисы свести к одному при помощи вращения вокруг общей точки? Оказывается, что все ортонормированные базисы распадаются на два класса: правый и левый.

Тройка векторов называется правой, если эти вектора, приведенные к одному началу, располагаются также как расставленные пальцы правой руки: большой палец – по первому вектору, указательный – по второму, средний – по третьему. Если смотреть во внутрь телесного угла, образованного этими векторами, то движение от первого ко второму, от второго к третьему будет совершаться против часовой стрелки. Обычно на практике рассматриваются только правые системы векторов.

3
Правая тройка	Левая тройка

Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим условиям:

а) | c | = | a |×| b |×sinj,

б) вектор с перпендикулярен к обоим векторам a и b,

в) упорядоченная тройка a, b, c – правая.

Векторное произведение обозначается символом a ´ b = [ a, b ].

Замечание. Отметим, что понятие векторного произведения также возникло в механике. Пусть F – сила приложенная к точке А, а r – радиус-вектор точки А относительно точки О. Тогда вектор M = r ´ F представляет собой момент силы относительно точки О.

Векторное произведение векторов обладает следующими свойствами:

1^о. a ´ b = – b ´ a (антикоммутативность),

2^о. k (a ´ b) = (k a) ´ b = a ´ (k b),

3^o. a ´(b+c) = a ´ b + a ´ c,

4^o. a ´ a = 0.

Пример 7.7. Вычислить выражение |(2 a + b)´(a +2 b)|, если | a |=1, | b |=2 и j = a ^ b =2p/3.

Решение. Раскроем скобки, учитывая свойства векторного произведения векторов:

(2 a + b)´(a +2 b) = 2 a ´ a + b ´ a +4 a ´ b +2 b ´ b = 0 – a ´ b +4 a ´ b + 0 = 3 a ´ b.

Далее из определения векторного произведения следует:

|(2 a + b)´(a +2 b)| = |3 a ´ b | =3| a || b |sinj = 3×1×2×sin120⁰ = 3Ö3. â

Из определения векторного произведения векторов, в частности, следует, что необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения:

a || b Û a ´ b = 0

Различные комбинации векторных произведений базисных векторов i, j, k можно записать следующим образом:

i ´ i = j ´ j = k ´ k = 0, i ´ j =× k, j ´ k ×= i, k ´ i = j.

Пример 7.8. Упростить выражение i ´(j+k)+ j ´(i+k).

Решение. Раскроем скобки и затем учтем соотношения между базисными векторами

i ´(j+k)+ j ´(i+k) = i ´ j+i ´ k + j ´ i+j ´ k = k–j–k+i = i–j. â

Теорема 7.3. Если два вектора a и b определены своими координатами в ортонормированном базисе: a ={ x ₁, y ₁, z ₁}, b ={ x ₂, y ₂, z ₂}, то векторное произведение вычисляется по формуле:

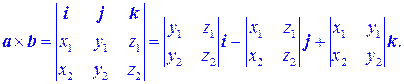
Доказательство. Действительно, учитывая, что a = x ₁ i + y ₁ j + z ₁ k, b = x ₂ i + y ₂ j + z ₂ k, получим

a ´ b = (x ₁ i + y ₁ j + z ₁ k) ´ (x ₂ i + y ₂ j + z ₂ k) = = (y ₁ z ₂– z ₁ y ₂) i – (x ₁ z ₂– z ₁ x ₂) j+ (x ₁ y ₂– y ₁ x ₂) k.

Далее, учитывая свойства определителей, получим искомую формулу. &

Геометрический смысл векторного произведения векторов a и b заключается в том, что модуль векторного произведения | a ´ b | равен площади параллелограмма, построенного на этих векторах.

Вопрос. При каком условии справедливо равенство (a ´ b)² = a ² b ².