Кривых распределения

Если изготовить партию деталей при практически неизменном технологическом процессе, то все размеры будут отличаться между собой. Это явление называется рассеиванием размеров. Рассеивание является результатом действия производственных погрешностей переменных по величине и знаку (в своем большинстве). Таким образом, получение действительного размера (параметра) изделия в некоторой части допуска является случайным событием, а сам размер случайной величиной.

Случайной величиной - называют величину, которая в результате опыта может принять то или иное значение, но неизвестно заранее, какое именно (по величине и направлению).

Математической характеристикой случайной величины является закон её распределения (т.е. соотношение, устанавливающее связь ме­жду возможными значениями случайной величины и соответствующими им вероятностями).

Закон распределения задается через интегральный закон (фун­кцию распределения) и дифференциальный (плотность вероятности).

Интегральным законом распределения случайной величины назы­вают функцию F(x), выражающую вероятность того, что X примет значение меньше данного значения x.

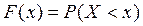(2.1)

Значения функции распределения находятся в интервале 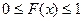. Например, если X время безотказной работы инструмента (стойкость),

Событие X<x означает отказ в течение времени x, а вероят­ность 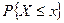- вероятность отказа за время х. Чем больше вре­мя работы, тем больше вероятность отказа инструмента. В начале работы x = 0, F(x) = 0, а при 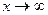, 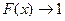. Статистически F(х) оценивается отношением числа инструментов n отказавших за время x, к общему числу инструментов N исправ­ных к началу работы x = 0. Дифференциальным законом распределения f(x) называют пер­вую производную от F(x)

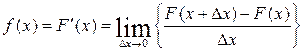(2.2)

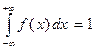(2.3)

График плотности вероятности f(x) называют кривой распределения

Рис. 2.1.

Вероятность попадания непрерывной случайной величины на за­данный интервал (а, b).

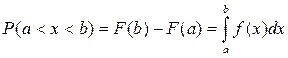(2.4)

Геометрически эта вероятность равна площади криволинейной трапеции, ограниченной кривой распределения осью абсцисс и прямых x = a и x = b. Большинство распределений может быть описано с помощью первых четырех моментов, причем начальному моменту первого порядка соответствует математическое ожидание m(х) или среднее значение:

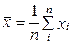; (2.5)

центральный момент второго порядка является дисперсией распределения х, где используют D=σ² или выборочная оценка S²:

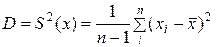; (2.6)

центральный момент третьего порядка характеризует асимметрию распределения х:

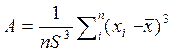; (2.7)

а четвертый момент - эксцесс или островершинность:

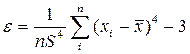(2.8)