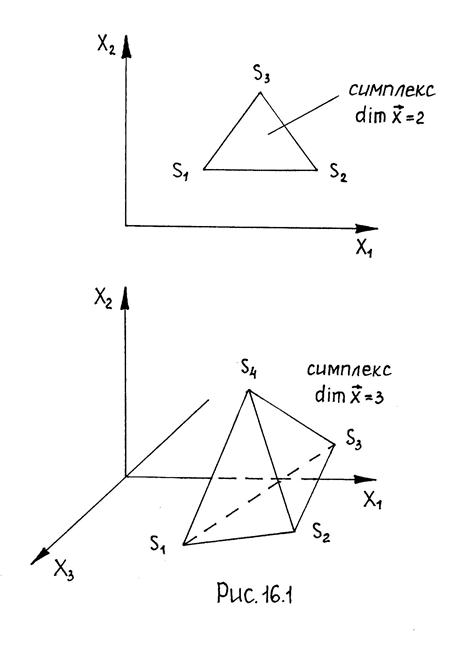
Симплекс - выпуклый многогранник в N-мерном пространстве имеющий N+1 вершину и грань. Рис 16.1. Рассмотрим способ решения задачи линейного программирования симплекс-методом. Пусть система ограничений задана в форме равенств
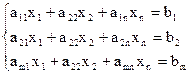 (1)
(1)
Пусть r<n, выразим r-независимых переменных через остальные n-r:
Хi, i=1,2….. -базисные
Xj, j= r+1,n – свободные
т.к свободным переменным можно придавать любые значения, то Xj=0 при j= r+1,n; Хi=Bi при i=1,r; col( b1 (x1),b2 (x2),…. br (xr),0(xr+1),0(xn) ) - первое базисное решение. Полученные решения являются допустимыми, т.к Xj=0 при j= r+1,n; Хi=Bi при i=1,r;
R=C1X1+C2X2+CnXn (3) подставим вместо базисных элементов их выражения через свободное R=Cо’+Cr+1’Xr+1+ Cr+2’Xr+2+Cn’Xn.
Для 1-ого базисного решения R=C0’ (5)
Далее переходим ко 2-му базисному решению таким образом, чтобы значение линейной формы r не увеличилось (пусть ищем минимум R). Переход осуществляется следующим образом – одна из базисных неизвестных заменяется свободной неизвестной и находится второе базисное решение. Этот процесс повторяется до тех пор, пока r не достигнет минимального значения.
Рассмотрим процедуру достижения минимума линейной формы:
R=3-X4+X5
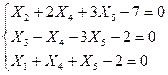
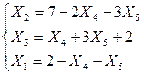
X=arg min R(X), rangA=3
1-е Б.р: Х= col (2(x1),7(x2),2(x3), 0(x4), 0(x5))
При переходе возникает вопрос об увеличении x4.
Х4 можно увеличивать только до двух, т.к. в противном x1 случае становится <0, что по условиям линейного программирования недопустимо.
2-е Б.р: Х= col( 0(x1),3(x2),4(x3),2(x4),0(x5) )
Выразим новые базисные переменные x2, x3,x4 через свободные x1,x5
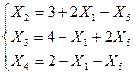
R=1+ x1+ 2x5
X(опт)=X(2-ого Б.р)= col ( 0(x1),3(x2),4(x3),2(x4),0(x5) ) – задача решена.
 2015-01-30
2015-01-30 340
340








