Рекомендуется повторить тему «делимость и остатки». (См. учебники: Миронов П.М. Арифметика. Изд. 3-е. – Чебоксары: Чуваш. кн. изд-во, 1999. – 319 с. (С. 105-121); Математика: Учеб. для 5 кл. общеобразоват. учреждений / Г.В. Дорофеев и др. – 4-е изд. – М.: Просвещение, 2001. – 368 с. (С. 141-153); Нурк Э.Р., Тельгмаа А.Э. Математика. 6 кл.: Учеб. для общеобразоват. учеб. заведений. – 2-е изд. – М.: Дрофа, 1997. – 224 с. (С. 5-11) и др.
Замечание.
1) Задачи, содержащие квадраты натуральных чисел решается перебором остатков от деления на 3 или на 4.
При делении на 3 и при делении на 4 квадраты дают остатки 0 и 1.
При делении на 8 квадраты дают остатки 0, 1, 4.
2) Задачи, содержащие кубы целых чисел решаются перебором остатков от деления на 7 или на 9.
При делении на 7 кубы целых чисел дают остатки 0, 1, 6.
При делении на 9 кубы целых чисел дают остатки 0, 1, 8.
Задача 1. Докажите, что уравнение 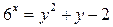 не имеет решения в целых числах.
не имеет решения в целых числах.
Решение. Сначала заметим, что 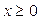 , так как если
, так как если 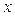 - целое отрицательное число, то
- целое отрицательное число, то 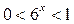 , а
, а 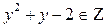 при
при 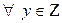 , тогда данное равенство невозможно.
, тогда данное равенство невозможно.
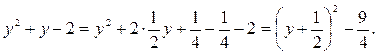
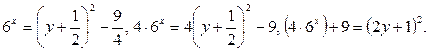 (*)
(*)
Известно, что любая натуральная степень числа 6 оканчивается на 6, а значит, 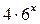 при любом натуральном
при любом натуральном 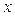 оканчивается на 4. Значит,
оканчивается на 4. Значит, 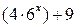 при любом натуральном
при любом натуральном 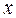 оканчивается на 3.
оканчивается на 3. 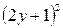 — квадрат целого числа, и значит, на 3 оканчиваться не может.
— квадрат целого числа, и значит, на 3 оканчиваться не может.
То есть левая часть уравнения (*) при 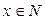 всегда оканчиваются на 3, а правая представляет собой квадрат целого числа, а он не может оканчиваться на 3. Значит, уравнение (*) не имеет решений в целых числах.
всегда оканчиваются на 3, а правая представляет собой квадрат целого числа, а он не может оканчиваться на 3. Значит, уравнение (*) не имеет решений в целых числах.
Обобщение: 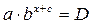 , где
, где 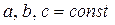 , а
, а 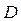 - квадрат целого числа. Например:
- квадрат целого числа. Например:
Задача 2. Решите в целых числах 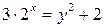 .
.
Решение. Если 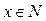 , то
, то 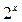 делится на четыре без остатка, а
делится на четыре без остатка, а 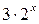 делится на три без остатка. А с учетом выше приведенного замечания мы знаем, что при делении на 3 и при делении на 4 квадраты дают остатки 0 и 1. В нашем случае
делится на три без остатка. А с учетом выше приведенного замечания мы знаем, что при делении на 3 и при делении на 4 квадраты дают остатки 0 и 1. В нашем случае 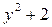 при делении на три или на четыре дает остаток либо 2, либо 3. Т.е. уравнение не имеет решений в целых числах.
при делении на три или на четыре дает остаток либо 2, либо 3. Т.е. уравнение не имеет решений в целых числах.
Ответ: Решений в целых числах нет.
Задача 3. Решите в целых числах 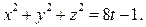
Решение. 1) Решение уравнения основано на утверждении что точные квадраты при делении на 8 могут давать остатки 0, 1, 4 (проверить самостоятельно).
2) Запишем данное уравнение в виде 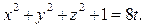
Правая часть данного уравнения делится на 8 без остатка, а левая часть при делении на 8 может давать следующие остатки: 1, 2, 3, 4, 5, 6, 7. Следовательно, данное равенство невозможно.
Ответ: Решений в целых числах нет.
Задача 4. Решите в целых числах 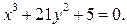
Решение. Так как 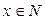 , то
, то 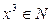 . Значит,
. Значит, 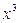 при делении на 7 может давать три различных остатка: 0, 1, 6.
при делении на 7 может давать три различных остатка: 0, 1, 6.
Так как 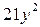 делится на 7 нацело при
делится на 7 нацело при 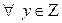 , то
, то 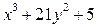 при делении на 7 может давать три различные остатка: 5, 6, 4; а значит, не может быть равным нулю, т. е. данное уравнение целых решений не имеет.
при делении на 7 может давать три различные остатка: 5, 6, 4; а значит, не может быть равным нулю, т. е. данное уравнение целых решений не имеет.
Ответ: Решений в целых числах нет.
Задача 5. Решите в целых числах 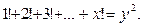
Решение. 1) Видно, что при а) 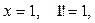 тогда
тогда 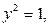
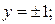 б)
б) 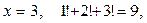 т.е.
т.е. 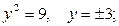
Получаем следующие решения: 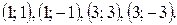
Заметим, что если 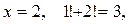 то
то 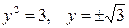 ‚ но
‚ но 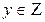 , значит, при
, значит, при 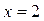 целочисленных решений нет.
целочисленных решений нет.
При 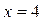 получаем
получаем 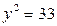 , а так как
, а так как 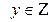 , то целочисленных решений при
, то целочисленных решений при 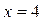 нет.
нет.
2) Если 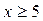 , то
, то 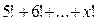 можно представить в виде
можно представить в виде 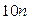 , где
, где 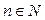 . Таким образом,
. Таким образом, 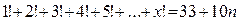 — число, оканчивающееся цифрой 3, значит, оно не может быть квадратом целого числа. Следовательно, при
— число, оканчивающееся цифрой 3, значит, оно не может быть квадратом целого числа. Следовательно, при 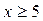 целых решений нет.
целых решений нет.
Ответ: 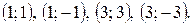
Задача 6. Докажите, что уравнение 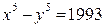 не имеет решений в целых числах.
не имеет решений в целых числах.
Решение. Предположим, что данное уравнение имеет решение в целых числах. Из того, что 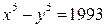 следует,
следует, 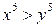 и
и 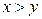 .
.
Запишем данное уравнение в виде 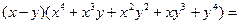
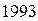 .
.
Так как 1993—число простое, а 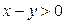 то
то  равно либо 1, либо 1993.
равно либо 1, либо 1993.
Если 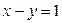 ,то
,то 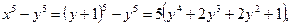 т.е. исходное уравнение примет вид
т.е. исходное уравнение примет вид 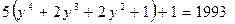 .
.
Видно, что левая часть уравнения при делении на 5 дает остаток 1, а правая, т. е. 1993, при делении на 5 дает остаток 3.
Если 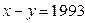 , то
, то 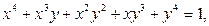 а это невозможно, т. к.
а это невозможно, т. к. 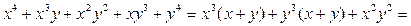
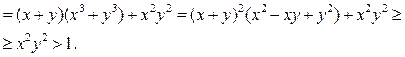
Следовательно, данное уравнение не имеет решений в целых числах.
Творческое задание: Составить авторские задачи по данному методу.
 2015-02-27
2015-02-27 1886
1886








