Производную сложной функции рассмотрим на примере функции двух переменных.
Пусть на множестве 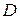 определена сложная функция
определена сложная функция 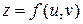 , где
, где 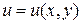 ,
, 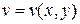 , и пусть функции
, и пусть функции 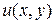 ,
, 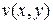 имеют в некоторой окрестности точки
имеют в некоторой окрестности точки 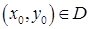 непрерывные частные производные, а функция
непрерывные частные производные, а функция 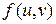 имеет непрерывные частные производные в некоторой окрестности точки
имеет непрерывные частные производные в некоторой окрестности точки 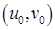 , где
, где 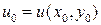 ,
, 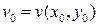 . Тогда сложная функция
. Тогда сложная функция 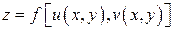 дифференцируема в точке
дифференцируема в точке 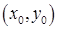 и её частные производные вычисляются по следующим формулам:
и её частные производные вычисляются по следующим формулам:
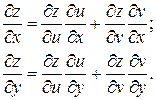
В частности, если функция 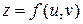 является функцией двух переменных, которые в свою очередь есть функции одной переменной
является функцией двух переменных, которые в свою очередь есть функции одной переменной 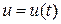 ,
, 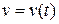 , то производная вычисляется по формуле
, то производная вычисляется по формуле
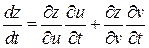 .
.
Пример 4.1. Найти частные производные функции 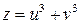 , где
, где 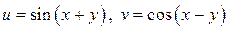 .
.
Решение. Имеем
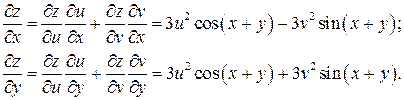
Пример 4.2. Найти производные 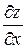 и
и 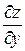 функции
функции 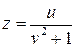 , где
, где 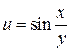 ,
, 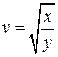 .
.
Решение. Используем правило дифференцирования сложной функции:
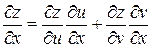 ,
, 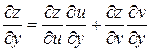 .
.
Найдем все частные производные, входящие в данные равенства:
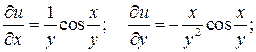
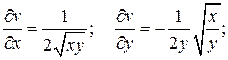
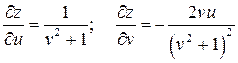 .
.
Тогда частные производные сложной функции 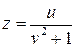 запишутся следующим образом:
запишутся следующим образом:
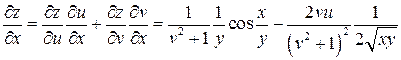 ;
;
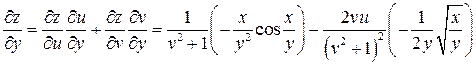 .
.
Подставив функции 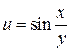 и
и 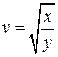 в найденные выражения, окончательно получим:
в найденные выражения, окончательно получим:
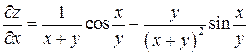 ;
;
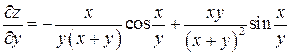 .
.
Доказать, что если 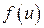 – произвольная дифференцируемая функция, то функция
– произвольная дифференцируемая функция, то функция 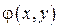 удовлетворяет следующему уравнению:
удовлетворяет следующему уравнению:
|
|
|
4.1. 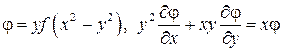 .
.
4.2. 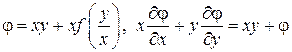 .
.
4.3. 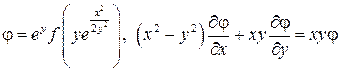 .
.
Найти производные первого и второго порядков от следующих сложных функций:
4.4. 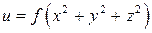 . .
| 4.5. 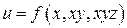 . .
|
Найти полные дифференциалы первого и второго порядков от следующих сложных функций:
4.6. 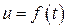 , где , где 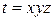 . .
| 4.7. 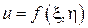 , где , где 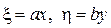 . .
|
4.8. 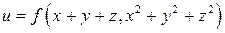 . .
|
4.9. 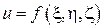 , где
, где 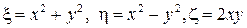 .
.
Найти 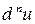 , если:
, если:
4.10. 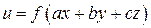 . .
| 4.11. 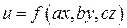 . .
|
4.12. Показать, что функция 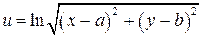 (
(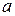 и
и 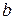 – постоянные) удовлетворяет уравнению Лапласа
– постоянные) удовлетворяет уравнению Лапласа
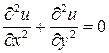 .
.
4.13. Показать, что функция 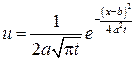 (
(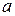 и
и 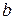 – постоянные) удовлетворяет уравнению теплопроводности
– постоянные) удовлетворяет уравнению теплопроводности
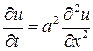 .
.
4.14. Упростить выражение 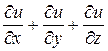 , если
, если
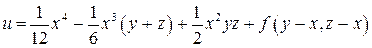 , где
, где 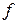 – дифференцируемая функция.
– дифференцируемая функция.
4.15. Пусть
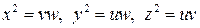
и
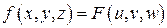 .
.
Доказать, что
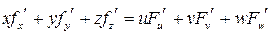 .
.
Предположив, что произвольные функции 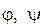 дифференцируемы достаточное число раз, проверить следующие равенства:
дифференцируемы достаточное число раз, проверить следующие равенства:
4.16. 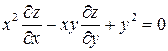 , если
, если  .
.
4.17. 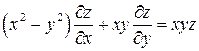 , если
, если 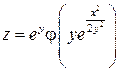 .
.
4.18. 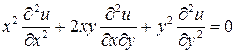 , если
, если 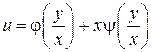 .
.
Ответы: 4.4. 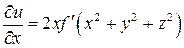 ;
; 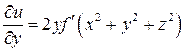 ;
;
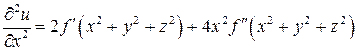 ;
; 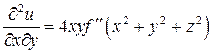 ;
;
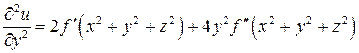 .
.
4.6. 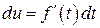 ,
, 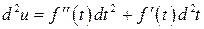 . 4.7.
. 4.7. 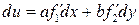 ,
,
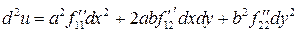 . 4.10.
. 4.10. 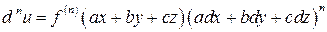 . 4.14.
. 4.14. 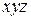 .
.
 2015-03-27
2015-03-27 1947
1947








