2015-03-08
3224
4.1.1. Пусть g - некоторое множество точек (на плоскости или в пространстве). Тогда говорят, что они образуют геометрическое место точек. Вообще говоря, g может быть произвольным. Но особый интерес представляют случаи, когда g образует на плоскости некоторую линию (или её часть), а в пространстве - линию или поверхность (или их части).
Часто это геометрическое место может быть описано словесно.
Примеры. 1. Геометрическое место точек на плоскости, равноудалённых от концов отрезка - это серединный перпендикуляр к отрезку.
2. Геометрическое место точек, равноудалённых от одной точки - это окружность (на плоскости) или сфера (в пространстве)
4.1.2. Предположим, g - геометрическое место точек, являющееся некоторой линией. Может оказаться, что координаты точек g связаны некоторым соотношением - уравнением
F (x, y)=0. (4.1)
Это уравнение называется общим уравнением линии g (при этом возможно, что некоторые слагаемые из левой части перенесены в правую).
Если из (4.1) y явно выражается через x в виде
y = f (x), (4.2)
то уравнение (4.2) называется явным уравнением линии g.
Наконец, координаты x и y точек линии могут быть функциями одного и того же аргумента:
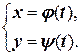(4.3)
Уравнения (4.3) называются параметрическими уравнениями линии g.
4.1.2. Для того, чтобы доказать, что некоторое из уравнений (4.1) - (4.3) является уравнением линии g, достаточно доказать, что, во-первых, координаты любой точки линии g удовлетворяют данному уравнению, и, во-вторых, обратно, любая точка, координаты которой удовлетворяют данному уравнению, принадлежит линии (то есть является точкой линии g).
Пример 3. Найдём различные уравнения окружности. Как отмечено выше, это - геометрическое место точек, равноудалённых от одной (фиксированной) точки. Возьмем систему координат так, чтобы начало координат совпало с данной фиксированной точкой. Пусть точки удалены от начала координат на расстояние R (то есть R - радиус окружности), X (x, y) - произвольная точка окружности. Тогда | OX |=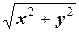 
, то есть 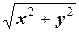= R. Возводя обе части этого уравнения в квадрат, получаем
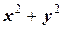= R 2. (4.4)
Обратно, пусть X (x, y) - точка, координаты которой удовлетворяют (4.4). Тогда | R |= 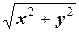. Но 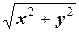- расстояние от точки X до начала координат O. И это справедливо для произвольной точки X, координаты которой удовлетворяют уравнению (4.4). Значит, 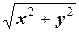- постоянное число и, следовательно, точки X равноудалены от точки O. Поэтому они лежат на окружности радиуса | R |.
Преобразуем уравнение (4.4):
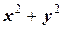= R 2 Û y 2= R 2- x 2 Û y =± 
.
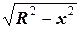Мы получили два уравнения вида (4.2). Первое - y = 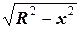описывает верхнюю часть окружности, второе y =- 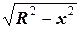- нижнюю.
Наконец,
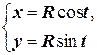(4.5)
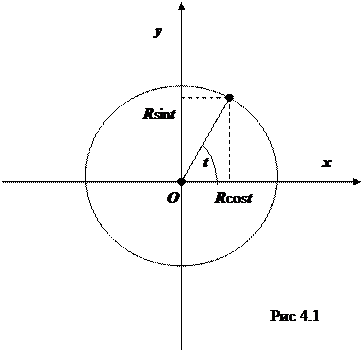
- параметрические уравнения окружности. Ясно, что при изменении параметра t в пределах [0, 2 p) точка с координатами (R cos t, R sin t) пробегает окружность радиуса R с центром (0, 0) (рис. 4.1)
4.1.3. От параметрических уравнений (4.3) часто можно перейти к уравнениям (4.1) и (4.2) и обратно. В первом случае достаточно из системы (4.3) исключить параметр t.
Например, если кривая задана уравнениями
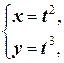
то выразив t через x (t =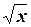 
) и подставив его в y, получаем y =(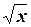)3= x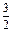 
, то есть y = x 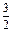- уравнение кривой в виде (4.2). Другой пример, возведём x и y в (3.5) в квадрат и сложим:
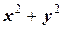= R 2cos2 t + R 2sin2 t = R 2(cos2 t +sin2 t)= R 2,
то есть 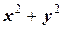= R 2, и мы получили уравнение окружности в виде (4.1).
4.1.4. В предыдущем параграфе мы ввели полярные координаты. Ясно, что во всех видах уравнений линии можно вместо прямоугольных координат x и y рассматривать полярные r и j. Тогда мы получим уравнения линии в полярных координатах. Уравнения (4.1) - (4.3) - это уравнения линии в прямоугольны координатах. Наиболее часто рассматривают уравнения в полярных координатах, аналогичные (4.1) и (4.2).
Например, уравнение окружности в полярной системе координат будет следующим: r = R. Это уравнение означает, что для любого j точка окружности отстоит от начала координат на постоянное число (то есть r - константа).
4.1.5. Преобразования координат иногда позволяют написать уравнение кривой (поверхности), исходя из известного его уравнения. Например, напишем уравнение окружности радиуса R с центром в точке (x 0, y 0), зная его уравнение (4.4) в случае, когда центр окружности совпадает с началом системы координат. Введём новую систему O ¢ x ¢ y ¢ с началом в центре окружности посредством параллельного переноса. Тогда в новой системе уравнение окружности имеет вид
x ¢ 2+ y ¢ 2= R 2. (4.6)
Так как связь между старыми и новыми координатами имеет вид
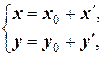
то x ¢ = x - x 0 и y ¢ = y - y 0, подставляя которые в (4.6) получаем (x - x 0)2+(y - y 0)2= R 2. Это и есть искомое уравнение окружности.
4.1.6. Упражнения. 1. Найти уравнение геометрического места точек:
a) Равноудалённых от точек A (-1, 1) и B (1, -1);
б)Равноудалённых от точек A (1, 1) и B (-1, -1);
в) Равноудалённых от точек A (2, 1) и B (4, -1).
Решение. а) Пусть X (x, y) - произвольная точка геометрического места точек. Тогда по условию задачи | XA |=| XB |. Выразим расстояния | XA | и | XB | и в координатах:
| XA |=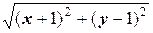 
, | XB |= 
.
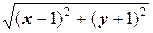Тогда | XA |=| XB | Û 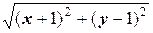= 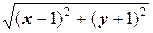. Возведём обе части последнего уравнения в квадрат: 
= 
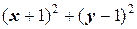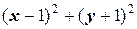. После раскрытия скобок и приведения подобных членов получаем x - y =0, или y = x. Как известно из школьного курса геометрии, это - уравнение биссектрисы первого квадранта ПДСК.
Обратно, если связь между координатами точек множества y = x, то, как уже мы заметили, они образуют прямую - биссектрису первого квадранта ПДСК. Очевидно, они равноудалены от точек A (-1, 1) и B (1, -1).
2. Исключить параметр из уравнения кривой:
а) x =3 t, y = t +2;
б) x =3 t 2, y = t +2;
в) x =3cos t +5, y =3sin t -2.
3. Уравнения геометрического места точек упражнения 1 написать в полярных координатах.
Решение. a) В уравнение y = x в прямоугольных координатах подставим вместо y и x их выражения через полярные координаты x = r cos j, y = r sin j и преобразуем: r sin j = r cos j Û tg j =1 (обе части разделили на r cos j).
Ответ: tg j =1.
