2015-04-01
871
При выполнении логических действий с понятиями из одного или нескольких понятий на основании преобразования их логической формы получают новое понятие. В формальной логике рассматривают только такие действия с понятиями, которые сводятся к преобразованию объемов этих понятий, то есть каждому действию с понятиями сопоставляется операция с классами или множествами (объемами этих понятий).
Пусть имеются два сравнимых понятия [, выражаемых предикаторами]: Аn(x1, …, xn) и Bn(x1, …, xn) (выражение в квадратных скобках в дальнейшем опускается). Сложением двух этих понятий называется такое логическое действие, при котором образуется новое понятие (сумма), выражаемое предикатором, полученным из предикаторов Аn(x1, …, xn) и Bn(x1, …, xn) с помощью коннектора неисключающей дизъюнкции; то есть сумма понятий, выражаемых предикаторами Аn(x1, …, xn) и Bn(x1,…,xn), выражается предикатором
Аn(x1,…, xn)Ú Bn(x1,…, xn);
при этом исходные понятия называются слагаемыми. Сложению понятий соответствует операция объединения классов; она обозначается знаком È. Таким образом,
|
|
|
Аn È Bn D {áx1, x2,..., xnñ½ Аn(x1, …, xn) Ú Bn(x1, …, xn)}
(знак D – «равно по определению» или «является сокращением для»: знак номинального определения).
Как видно из определения сложения понятий, объединение Аn È Bn двух классов Аn и Bn содержит все те и только те элементы из области определения понятий, которые принадлежат классу Аn или принадлежат классу Bn (или неисключающее).
Умножением двух понятий Аn(x1, …, xn) и Bn(x1, …, xn) называется такое логическое действие, при котором образуется новое понятие (произведение), выражаемое предикатором, полученным из предикаторов Аn(x1, …, xn) и Bn(x1, …, xn) с помощью коннектора конъюнкции; то есть произведение понятий, выражаемых предикаторами Аn(x1, …, xn) и Bn(x1, …, xn), выражается предикатором
Аn(x1, …, xn) Ù Bn(x1, …, xn);
при этом исходные понятия называются сомножителями. Умножению понятий соответствует операция пересечения классов; она обозначается знаком Ç. Таким образом,
Аn Ç Bn D {áx1, x2,..., xnñ½ Аn(x1, …, xn) Ù Bn(x1, …, xn)}.
Как видно из определения умножения понятий, пересечение Аn Ç Bn двух классов Аn и Bn содержит все те и только те элементы из области определения понятий, которые принадлежат классу Аn и принадлежат классу Bn.
Отрицанием понятия Аn(x1, …, xn) называют логическое действие, при котором получают новое понятие, выражаемое предикатором ØАn(x1, …, xn); результат действия отрицания понятия тоже называют отрицанием. Отрицанию понятия соответствует операция с классами, которая называется дополнением класса до универсума; то же название используют для обозначения результата этой операции. Дополнение класса до универсума обозначается с помощью символа ¯ ; таким образом, объем отрицания понятия Аn(x1, …, xn) выражается следующим образом: Ān D {áx1, x2,..., xnñ½ ØАn(x1, …, xn) }.
|
|
|
Вычитанием понятия Bn(x1,…, xn) из понятия Аn(x1, …, xn) называют умножение понятия Аn(x1, …, xn) на отрицание понятия Bn(x1, …, xn); то есть разность (результат вычитания) двух понятий: Аn(x1, …, xn) (уменьшаемого) и Bn(x1, …, xn) (вычитаемого), выражается предикатором
Аn(x1, …, xn) Ù Ø Bn(x1, …, xn).
Вычитанию понятий соответствует операция с классами, которая носит то же название: вычитание классов (множеств). Таким образом, результат вычитания множества Bn из множества Аn совпадает с результатом пересечения множества Аn с дополнением до универсума множества Bn:
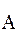n Ç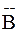 
n D {áx1, x2,..., xnñ½ Аn(x1, …, xn) Ù Ø Bn(x1, …, xn)}
При записи операций с классами действует соглашение о скобках для знаков Ú, Ù, Ø, перенесенное на знаки È, Ç и ¯ соответственно.
На основании определения логических действий с понятиями могут быть доказаны законы логики классов.
Пусть Аn , Bn, Сn – объемы сравнимых понятий Аn(x1, …, xn), Bn(x1, …, xn), Сn(x1, …, xn) соответственно; знаки È, Ç, ¯, Ø, 1 – знаки объединения, пересечения, дополнения до универсума, объема пустого понятия и объема универсального понятия соответственно. Тогда для любых Аn , Bn, Сn имеют место следующие равенства:
 | |||||||
 |  | | |||||
1.1. 
(Аn Ç Bn) = Аn È Bn законы де Моргана
1.2. (Аn È Bn) = Аn Ç Bn дляклассов,
|
1.3. Аn = Аn – закон двойного отрицания для классов,
1.4. Аn = Аn – закон тождества для классов,
1.5. Аn Ç Bn = Bn Ç Аn – коммутативность Ç,
1.6. Аn È Bn = Bn È Аn – коммутативность È,
1.7. (АnÇBn)ÇСn = АnÇ(BnÇСn) – ассоциативность Ç,
1.8. (АnÈBn)ÈСn = АnÈ(BnÈСn) – ассоциативность È,
1.9. АnÇ(BnÈСn)=(АnÇBn)È(АnÇСn) – дистрибутивность Ç относительно È,
1.10.АnÈ(BnÇСn)=(АnÈBn)Ç(АnÈСn) – дистрибутивность È относительно Ç,
1.11. Аn Ç (Аn È Bn) = Аn – поглощение,
1.12. Аn È (Аn Ç Bn) = Аn – поглощение,
1.13. Аn Ç Аn = Аn – идемпотентность,
1.14. Аn È Аn = Аn – идемпотентность,
1.15. а) Аn Ç 1 = Аn; б) Аn Ç Ø = Ø – законы для нуля и
1.16. а) Аn È 1 = 1; б) Аn È Ø = Аn единицы.
Булевой алгеброй называют всякое множество с выделенными на нем двумя элементами («нулем» и «единицей») и определенными на нем двумя двуместными операциями («сложение» и «умножение») и одноместной операцией («отрицание»), удовлетворяющими вышеперечисленным законам. Таким образом, множество всех классов с пустым (Ø) и универсальным (1) классами, на котором определены операции объединения (È), пересечения (Ç), дополнения до универсума (¯), удовлетворяющие законам логики классов, является примером булевой алгебры (с Ø и 1 в качестве«нуля» и «единицы» и операциями «дополнения до универсума», «объединения», «пересечения» в качестве «отрицания», «сложения» и «умножения» соответственно).
Обобщением понятия Аn(x1, …, xn) называется логическое действие, при котором от понятия Аn(x1, …, xn) переходят к родовому понятию Bn(x1, …, xn), то есть такому понятию, для которого выполнено соотношение: Аn Ì Вn.
Ограничением понятия Аn(x1, …, xn) называется логическое действие, при котором от понятия Аn(x1, …, xn) переходят к видовому понятию Bn(x1, …, xn), то есть такому понятию, для которого выполнено соотношение: Вn Ì Аn.
При обобщении понятия объем его увеличивается за счет удаления некоторого признака из содержания понятия. При ограничении понятия объем его уменьшается за счет включения в его содержание дополнительного признака.
Делением понятия Аn(x1, …, xn) в логике называют логическое действие, при котором объем понятия Аn(x1, …, xn) разбивается на m непересекающихся классов (m=2,…) путем добавления к содержанию понятия дополнительных признаков или их отрицаний. Понятие, объем которого разбивается, называется делимым понятием. Понятия, объемами которых являются непересекающиеся классы, называются членами деления. Признак, с помощью которого производится разбиение объема делимого понятия на непересекающиеся классы, называется основанием деления. Таким образом, деление понятия можно представить следующей схемой:
|
|
|
Аn(x1, …, xn) делимое понятие,
основание деления,
B1n(x1, …, xn)
B2n(x1, …, xn) члены деления.
…
Bmn(x1, …, xn)
Различают два вида деления: дихотомическое деление и деление по видоизменению основания. При дихотомическом делении объем делимого понятия Аn(x1, …, xn) делится на два непересекающихся подмножества, одно из которых является объемом некоторого видового (по отношению к Аn(x1, …, xn)) понятия Вn(x1, …, xn), а другое – объемом Аn(x1, …, xn)Ù Ø Bn(x1, …, xn). Таким образом, члены дихотомического деления получаются из делимого понятия путем добавления в содержание делимого понятия признака, являющегося основанием деления, или его отрицания.
Пример 3.1. Примером дихотомического деления является следующее деление:
х – человек: А1(x) делимое понятие;
основание деления: пол;
х – человек мужского пола: В1(x) члены деления.
х – человек немужского пола: Ø В1(x)
ОО: живые организмы
В1
 | |||
 | |||
При делении по видоизменению основания в качестве основания деления используются предметно-функциональные характеристики элементов объема делимого понятия.Предметно-функциональные характеристики представляют собой понятия, то есть предикаты, полученные из операций или предикатов, определенных на области определения делимого понятия; они записываются в ЯЛФРТ предикаторами, полученными из операторов или предикаторов (см. тему 2, стр.59-61).
