Второй способ

Поскольку модель (3.5.2)

j (х, c ₀, c ₁, c ₂, …, c_m) = c ₀j₀(х) + c ₁j₁(х) + c ₂j₂(х) + … + c_m j _m (х)

должна соответствовать y_i = f (x_i), i = 0, 1, 2, …, n – данным, представленным в узлах сетки

h _x = { x_i / x_i = x_{i – 1} + h_i, h_i > 0, i = 1, 2, 3, …, n; x ₀ = a, x_n = b },

то значения модельных параметров вполне целесообразно выбирать из интерполяционных условий

j (х_i, c ₀, c ₁, c ₂,…, c_m) = y_i, i = 0, 1, 2, …, n.

Эта система уравнений является системой линейных уравнений, поскольку модель j (х_i, c ₀, c ₁, c ₂, …, c_m) линейна относительно модельных параметров c ₀, c ₁, c ₂,…, c_m. Запишем ее в детальной форме:

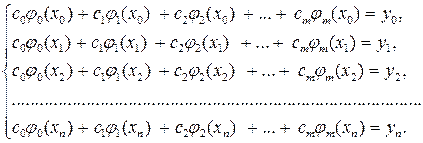(3.5.11)

Матрица системы (3.5.11) – прямоугольная n×m матрица:

А = 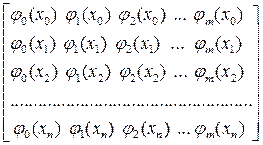(3.5.12)

Система линейных уравнений (3.5.11) является переопределенной
с матрицей A, имеющей полный столбцовый ранг, так как по предположению m < n, а базисные функции j₀(х), j₁(х), j₂(х), j _m (х) линейно независимы. Как известно, для переопределенных систем линейных уравнений ищется так называемое обобщенное решение, которое обеспечивает минимум суммы квадратов невязок

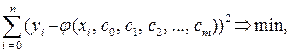
что соответствует условию (3.5.1).

Другими словами, значения модельных параметров 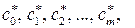определяющие наилучшее среднеквадратическое приближение
j (х, 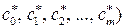в соответствии с условием (3.5.1), могут быть определены как компоненты обобщенного решения переопределенной системы (3.5.11).

Для построения обобщенного решения системы (3.5.11) может быть использована первая трансформация Гаусса. В этом случае (3.5.11) преобразуется в систему (3.5.9). Действительно, применяя к системе (3.5.11) первую трансформацию Гаусса, получаем систему линейных уравнений
с квадратной неособенной матрицей

А ^т А c = А ^т y.

Поскольку в обозначениях (3.5.7) и (3.5.8) А ^т y = g, а А ^т А = Г, полученная система эквивалентна системе (3.5.9).

Так как первая трансформация Гаусса ухудшает обусловленность системы линейных уравнений, то применение такого подхода не всегда целесообразно. В ряде случаев систему (3.5.11) предпочтительнее решать с помощью любого другого из известных методов, например с использованием ортогональных преобразований, что обеспечит большую устойчивость вычислительного процесса. В последнем случае процесс построения наилучшей в смысле метода наименьших квадратов аппроксимации таблично заданной на отрезке [ a, b ] функции можно представить в виде следующего алгоритма.