Билет 21 Теорема 1

Последовательность чисел 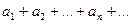(1)

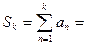
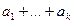
Опр. 1: 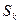называется частичной суммой ряда (1): .

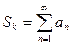Опр. 2: 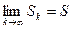. Если существует предел 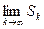(конечный или бесконечный), то этот предел называется суммой ряда.

Опр. 3: Пусть 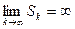или не существует. Тогда говорят, что ряд (1) расходится. Если же существует конечная сумма 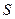, тогда говорят, что ряд (1) сходится, и его сумма равна .

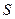Теорема 1. Пусть 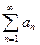(1). Пусть ряд (1) сходится, тогда сходится и ряд 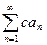, причем сумма

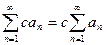, (где ).

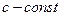Теорема 2. 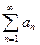(А), 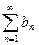(В). Пусть ряды (А) и (В) сходятся., и их суммы равны А и В.

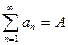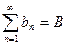, . Тогда сходятся ряды 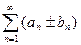и их суммы равны :

= .

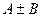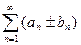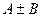Теорема 3. (принцип сходимости Коши). 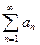(1). Ряд (1) сходится :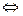

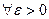
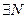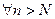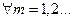, выполнено = .

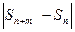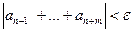Теорема 4. (необходимое условие сходимости числового ряда). Пусть ряд 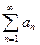сходится. Тогда

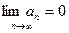- необходимое условие сходимости.

БИЛЕТ 22.

Гармонический ряд 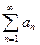. Пусть 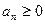. Такой ряд называется положительным.

Теорема 1. Положительный ряд всегда имеет сумму. Эта сумма бесконечна (и тогда ряд расходится), если 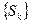не ограничена сверху; сумма конечна, (и тогда ряд расходится), если 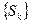ограничена сверху.

Теорема 2: Гармонический ряд 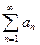расходится.

БИЛЕТ 23.

Теорема. Пусть есть обобщенный гармонический ряд 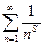. Тогда:

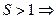ряд сходится, ряд расходится.

БИЛЕТ 24.

Теорема 1 (признак сравнения).

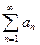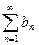(А), (В). Пусть начиная с некоторого номера выполняется (*)

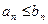Тогда если ряд (А) расходится, то расходится и ряд (В). Если же ряд (В) сходится, то сходится и ряд (А).

Теорема 2 (признак сравнения в предельной форме).

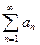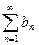(А), (В). Пусть 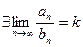, но существующий предел 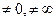. Тогда ряды (А) и (В) либо одновременно сходятся, либо одновременно расходятся.

Теорема 3 (признак сравнения).

Пусть начиная с некоторого номера 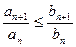. Тогда, если сходится ряд (В), то сходится и ряд (А). Если же расходится ряд (А), то расходится и ряд (В).

БИЛЕТ 25.

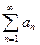(А)

Теорема 1: (радикальный признак Коши):

Пусть, начиная с некоторого номера выполняется 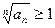(1). Тогда ряд (А) расходится. Если же, начиная с некоторого номера, 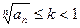(2), тогда ряд (А) расходится.

Теорема 2 (радикальный признак Коши в предельной форме).

Пусть 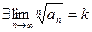. Если 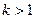, то ряд (А) расходится. Если 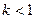, то ряд (А) сходится.

БИЛЕТ 26.

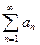(А)

Теорема 1 (признак Даламбера):

Пусть, начиная с некоторого номера, выполняется 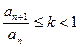(1). Тогда ряд (А) сходится. Если же, начиная с некоторого номера выполнено 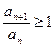(2), то ряд (А) расходится.

Теорема 2 (признак Даламбера в предельной форме).

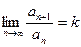. Если 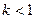, то ряд (А) сходится. Если 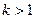, то ряд (А) расходится.

Признак Раабе (без доказательства).

Пусть, начиная с некоторого номера выполнено неравенство 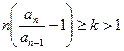. Тогда ряд (А) сходится. Если же начиная с некоторого номера 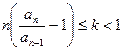, то ряд (А) расходится.

БИЛЕТ 27.

Теорема (интегральный признак сходимости).

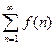(*). Пусть 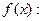1) определена при 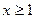, 2) непрерывна, 3) 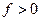, 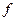монотонно убывает. Пусть также 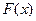- некоторая первообразная функции . Тогда, если 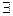конечный предел 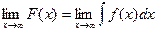, то ряд (*) сходится. Если же 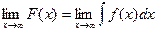не существует или равен 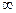, то ряд (*) расходится.

БИЛЕТ 28.

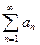(А) 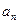- произвольного знака. (

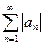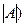
Утверждение: Пусть ряд (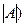 сходится. Тогда сходится и ряд (А).

Определение: Если сходится ряд 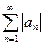, то говорят, что ряд 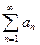сходится абсолютно. Из утверждения 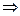, что если ряд сходится абсолютно, то он сходится и сам по себе.

Определение: Если расходится ряд 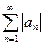, но ряд 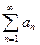сходится, то говорят, что ряд

БИЛЕТ 29.

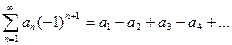(А) Такой ряд называется знакопеременным.

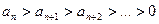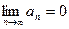Теорема (признак Лейбница). Пусть: 1) 2) . Тогда ряд (А) сходится.

Следствие: 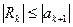. 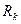имеет знак 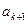. 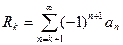- остаток ряда Лейбница.

БИЛЕТ 30.

Теорема (о перестановке членов абсолютно сходящегося ряд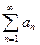а).

(А) 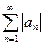(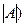. Пусть ряд (А) сходится абсолютно. Тогда любой ряд, полученный из ряда (А) перестановкой его членов, сходится абсолютно к тому же числу.

Теорема Римана (без доказательства).

Пусть ряд 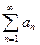сходится, но только условно. Тогда для любого заданного числа 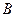(в том числе 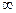) можно так переставить члены ряда 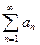, что новый ряд будет сходиться к числу .

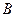БИЛЕТ 31.

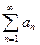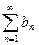Теорема 1. (А), (В). Пусть ряды (А) и (В) сходятся, тогда сходятся и ряды 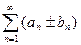, , 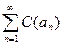где 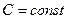, причем:

= ,

= .

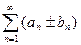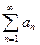
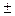
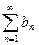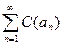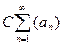Теорема 2. 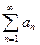(А), 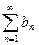(В). Пусть ряды (А) и (В) сходятся абсолютно. , .

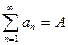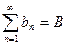Тогда ряд 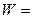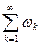, где 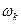- всевозможные произведения вида 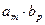сходятся абсолютно к числу .

=

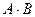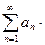
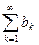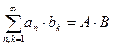
БИЛЕТ 32.

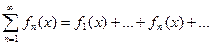- функциональный ряд (1).

Определение: Пусть сходится числовой ряд 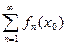. Поточечная сходимость. Тогда говорят, что функциональный ряд (1) сходится в точке 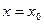. Если функциональный ряд (1) сходится 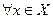(некоторое множество), то говорят, что функциональный ряд (1) сходится на 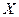. 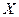- область сходимости функционального ряда (1).