2.1. Характеристики, отражающие «центростремительные» тенденции.
Первая статистическая характеристика – это средняя арифметическая взвешенная, затем мода и медиана.
Все характеристики рассчитываются по вариационному ряду. Приведем его несколько в ином виде.
Вариационный ряд по диаметру (частоты и частости).
Таблица 3.
| № | Интервал по диаметру | Срединное значение интервала (классовая варианта) xi (см) | Частота встречаемости классовой варианты ni (шт) | Частость классовой варианты
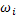 (доля). (доля).
|
| 1. | 6,0 – 10,0 | 0,06 | ||
| 2. | 10,1 -14,0 | 0,16 | ||
| 3. | 14,1 – 18,0 | 0,32 | ||
| 4. | 18,1 – 22,0 | 0,24 | ||
| 5. | 22,1 – 26,0 | 0,12 | ||
| 6. | 26,1 – 30,0 | 0,06 | ||
| 7. | 30,0 – 34,0 | 0,04 | ||
| 1,0 |
Формула для расчета средней арифметической взвешенной
(1)
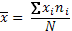
где: 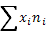 сумма значений классовых вариант, умноженных на соответствующие частоты, N =
сумма значений классовых вариант, умноженных на соответствующие частоты, N = 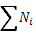 - объем выборки.
- объем выборки.
Другой расчет для определения средней основан на вероятностной природе выборки. Частости являются долями присутствия значений признака в общем объеме выборки, т.е. частями от общего объема, а значения отражают вероятность исхода испытания для значения признака (классовой варианты), связанного с этой частостью. Поскольку сумма частостей составляет полную группу событий, то среднее значение можно получить исходя из формулы (1)
|
|
|
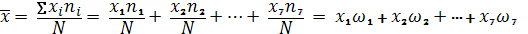 (2)
(2)
Читается эта формула так: среднее значение случайной величины равно сумме произведений всех ее возможных значений на их вероятности.
Модой (Mo) называют варианту, которая имеет наибольшую частоту. В нашем примере она равна 16. В случае равных интервалов ее значение определяют по классовой варианте. Однако, в силу того, что в границах модального интервала имеет место разброс значений признака, а также сама частота интервала случайна и связана с частотами соседних классов, точное значение Mo рассчитывают по формуле:
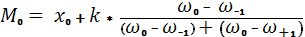 (3)
(3)
где: Xo – нижняя граница модального класса,
K – величина интервала,
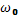 – частость модального класса.
– частость модального класса.
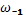 – частость класса, предшествующего модальному.
– частость класса, предшествующего модальному.
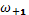 – частость класса последующего за модальным.
– частость класса последующего за модальным.
Медианой (Me) называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. То есть в обе стороны от медианы находятся равные количества частот. Медиану вариационного ряда находят следующим образом:
- Находим класс, которому принадлежит медиана. Для этого в ВР (таблица 2) рассматривают колонку накопленных частот. По значениям накопленных частот выбирают класс интервала. Первое значение накопленной частоты, которое больше половины объема выборки соответствует классу интервала, в котором присутствует медиана. В нашем примере первое значение накопленной частоты большее 1/2N (25) находится в третьем классе (27). Значит медиана находится в этом классе.
- Находим значение медианы по формуле:
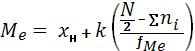 (3)
(3)
|
|
|
где: 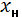 – нижняя граница класса интервала, содержащего медиану.
– нижняя граница класса интервала, содержащего медиану.
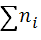 – накопленная частота, предшествующая медианному классу.
– накопленная частота, предшествующая медианному классу.

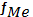 - частота медианного класса.
- частота медианного класса.
Отношение между средней арифметической, модой и медианой выражается формулой:
(4)
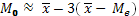 , откуда
, откуда
(5)
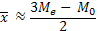
Эти формулы справедливы для достаточно симметричных вариационных рядов.
Необходимым условием симметричности ВР является равенство:
(6)
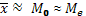
Нарушение приведенных соотношений свидетельствует о неравномерном распределении частот ВР относительно 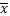 .
.
Для распределений с правосторонней асимметрией справедливо неравенство:
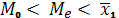 , с левосторонней -
, с левосторонней -  .
.
2.2. Характеристики изменчивости признака.
При построении ВР была использована разность между максимальной и минимальной величинами признака (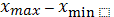 ). Эта разность называется размахом варьирования (изменчивости) и является одной из характеристик изменчивости. Размах варьирования – это, собственно, границы диапазона значений, применяемые признаком. Чем больше этот диапазон, тем сильнее варьирует признак.
). Эта разность называется размахом варьирования (изменчивости) и является одной из характеристик изменчивости. Размах варьирования – это, собственно, границы диапазона значений, применяемые признаком. Чем больше этот диапазон, тем сильнее варьирует признак.
Следующей рассчитываемой в работе характеристикой изменчивости является дисперсия. По определению – это средний квадрат отклонений от средней величины. Формула для ВР:
(7)
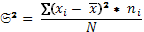
где:  – последовательные слагаемые отклонения каждой классовой варианты от среднего значения ВР:
– последовательные слагаемые отклонения каждой классовой варианты от среднего значения ВР: 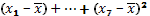 .
.
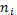 – частота соответствующего класса интервала.
– частота соответствующего класса интервала.
Если из значения дисперсии извлечь корень, то получается ещё одна характеристика изменчивости, которая называется средним квадратическим отклонением:
(8)
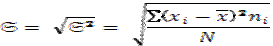
Дисперсию и, следовательно, среднеквадратическое отклонение можно вычислить также и по формуле:
(9)
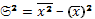 ,
,
где: 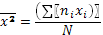
Размерность среднеквадратического отклонения такая же, как в исходных данных.
Перечисленные характеристики изменчивости признака – величины именованные. Это не всегда удобно, особенно, когда нужно сравнивать выборки с различной размерностью признака. Поэтому используется относительный показатель изменчивости, который называется коэффициентом вариации:
(10)
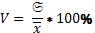
При величине коэффициента вариации примерно до 33% распределение можно считать достаточно однородным. Естественно, чем меньше V, тем совокупность однороднее. При V>50% использование этого коэффициента бессмысленно. Во всех случаях среднеквадратическое отклонение является более надежной оценкой изменчивости.
Еще один показатель изменчивости ряда распределения, тоже относительный, - нормированное отклонение:
(11)
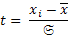
Нормированное отклонение производит оценку отклонения любой варианты от среднего значения ряда в размерности 𝔖. С помощью нормированного отклонения можно оценить положение каждой варианты в ряду распределения. Действительно, из формулы следует, что каждая варианта (xi) связана с определенным значением t, которое указывает ее положение в ВР и на кривой распределения. В нашем примере, если пересчитать значения классовых интервалов в долях 𝔖, получим следующие t-распределение.
Таблица 4.
t -распределение диаметров по эмпирическим данным.
| Классовая варианта, см | |||||||
| Критерий t, доли | -1,87 | -1,16 | -0,45 | 0,27 | 0,98 | 1,70 | 2,41 |
Это распределение показывает, что деревья с диаметром 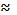 8 находятся в левой части кривой полигона на расстоянии 1,87 𝔖 от
8 находятся в левой части кривой полигона на расстоянии 1,87 𝔖 от 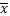 . Деревья с диаметром 24 находятся от
. Деревья с диаметром 24 находятся от 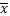 на расстоянии 0,98𝔖 в правой части полигона распределения и т.д.
на расстоянии 0,98𝔖 в правой части полигона распределения и т.д.
2.3. Оценка формы эмпирического распределения.
Выборки, особенно малочисленные (<30ед.), как правило, по форме кривой распределения значительно отличаются от теоретической кривой нормального распределения.
|
|
|
Несимметричность эмпирического распределения можно оценить по характеру распределения частот в классах ВР. Графически она видна по форме полигона и гистограммы распределений. Количественная ее мера рассчитывается через специальные характеристики: асимметрия и эксцесс.
Асимметрия рассчитывается по формуле:
(12)
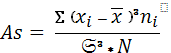
Если коэффициент равен нулю – ряд симметричен. Отрицательное значение As указывает не левостороннюю асимметрию, когда относительно модального класса левая часть кривой больше вытянута чем правая. Наоборот, когда более вытянута правая часть кривой распределения, говорят о правосторонней асимметрии. Коэффициент асимметрии не имеет ни верхней, ни нижней границы. Однако, на практике для умеренно асимметричных рядов он редко бывает больше единицы.
Коэффициент эксцесса характеризует форму вершины эмпирического распределения, он рассчитывается по формуле:
(13)
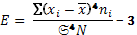
Положительное значение коэффициента эксцесса указывает на островершинность распределения. В этом случае классы с большими частотами группируются вокруг модального класса. Такого рода эксцесс называется положительным, а его коэффициент имеет знак «+». Положительный эксцесс не ограничен верхним пределом, но степень его соответствия нормальному распределению будет показана ниже. Отрицательное значение эксцесса указывает на плосковершинность распределения, имеет отрицательное значение, предельная величина которого равна – 2.
В заключение раздела приведем сводную таблицу, по которой удобно рассчитывать почти все приведенные выше статистические характеристики выборочной совокупности.
Таблица 14. Сводная таблица расчетов основных характеристик вариационного ряда.
| № | Классовая варианта
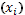
| Частота
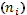
| Отклонение
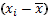
| Отклонение с учетом частоты
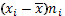
| Квадрат отклонения с учетом частоты
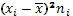
| Куб отклонения с учетом частоты
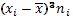
| Четвертая степень отклонения с учетом частоты
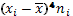
|
| -10,53 | - 31,59 | 332,6427 | (8-18,53)33 | (8-18,53)43 | |||
| -6,53 | -52,24 | 341,127 | - - - | - - - | |||
| - 2,53 | -40,48 | 102,4144 | - - - | - - - | |||
| 1,47 | 17,64 | 25,9308 | - - - | - - - | |||
| 5,47 | 32,82 | 179,5254 | - - - | - - - | |||
| 9,47 | 28,41 | 269,0427 | (28-18,53)33 | (28-18,53)43 | |||
| 13,47 | 26,94 | 362,8818 | - - - | - - - | |||
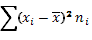
| 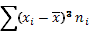
| 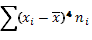
|
По данным колонок 6, 7, 8 рассчитывают соответственно дисперсию (𝔖2), асимметрию (As) и эксцесс (E) по формулам, приведенным в разделе.
|
|
|
В такой же последовательности строят ВР по высоте.
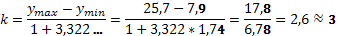
Таблица 2.
Вариационный ряд по высоте.
| № | Классовый интервал | Срединное значение интервала yi | Частота |
| 7,5 - 10,5 |
 4 4
| ||
| 10,6 – 13,5 |
 4 4
| ||
| 13,6 - 16,5 |
 6 6
| ||
| 16,6 – 19,5 |
  15 15
| ||
| 19,6 – 22,5 |
  15 15
| ||
| 22,6 – 25,5 |
 5 5
| ||
| 25,6 – 28,5 |
 1 1
| ||
2.4. Ошибки выборочных характеристик и оценка параметров генеральной совокупности.
Рассчитанные в предыдущем разделе характеристики выборочной совокупности называются точечными. Это название используется для разделения оценок выборочной и генеральной совокупностей. Точечная оценка (характеристика) выборки (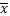 , 𝔖, V) в пределах самой выборки исчерпывающее ее описывает. Однако, сами характеристики выборки существенно зависят от ее объема: для выборок разного объема перечисленные характеристики будут иметь разные значения. Поэтому для характеристики параметров генеральной совокупности применяются интервальные оценки.
, 𝔖, V) в пределах самой выборки исчерпывающее ее описывает. Однако, сами характеристики выборки существенно зависят от ее объема: для выборок разного объема перечисленные характеристики будут иметь разные значения. Поэтому для характеристики параметров генеральной совокупности применяются интервальные оценки.
Для интервальной оценки параметров генеральной совокупности необходим предварительный расчет ошибок характеристик выборочной совокупности. Эти ошибки называются ошибками выборочности, чем подчеркивается зависимость их величин от размера выборки. Зависимость – обратная: чем больше объем выборки, тем меньше ее ошибка относительно величины аналогичного генерального параметра.
Для средней арифметической выборки ошибка выборочности равна:
(14)
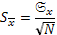
где: 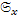 – среднеквадратическое отклонение выборки, составленной из
– среднеквадратическое отклонение выборки, составленной из
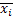 (i от 1 до N), но берется 𝔖 из исследуемой выборки, N – объем этой выборки.
(i от 1 до N), но берется 𝔖 из исследуемой выборки, N – объем этой выборки.
Выборочная ошибка среднеквадратического отклонения, т.е. оценка аналогичного параметра генеральной совокупности рассчитывается по формуле:
(15)
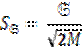
Ошибка коэффициента вариации
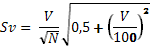
Ошибка асимметрии
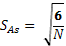
Ошибка коэффициента эксцесс
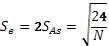
Перечисленные ошибки зависят от объема совокупности, по которой они рассчитываются. Отсюда следует, что они обладают вероятностной природой. Значит, говорить о точности статистических оценок можно только с учетом вероятности распределения частот на графике-полигоне (гистограмме), строго говоря, на графике плотности распределения вероятности.
Нормированная кривая распределения приведена на рисунке 5. Ось абсцисс представлена собственно тремя осями: первая – ось значений признака, вторая – ось значений признака, пересчитанных в 𝔖 - мах, третья – ось значений признака, пересчитанная в долях нормированных отклонениях.
--граффик.
Ось Х соответствует значениям таблицы ВР. Особенностью нормального распределения является закономерность распределения частостей по диапазонам 𝔖 или t. Для нормального распределения всегда в диапазоне –𝔖 - +𝔖 лежит 68,3% вариант общего объёма значений признака, от –2𝔖 до 2𝔖- 95,5%, от -3𝔖 до 3𝔖 - 99,7% всех вариант совокупности.
Таким образом, единицу нормированного отклонения 𝔖, так же как и t, можно свзять с вероятностью значений признака. Это следует также из формулы нормированного отклонения, записанной в таком виде:
(19)
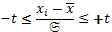
После преобразования получим:
(20)
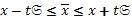
Это и есть доверительный интервал, в котором будет находится значение средней величины любой выборки с вероятностью, определяемой величиной t. При t=1,00 мы будем иметь 68% вероятность, при t=1,96(2,0) – вероятность равна 95,5%, при t=3 диапазон возможных значений средней величины перекрывает 99,7% всех возможных значений. Это неравенство справедливо и в том случае, если речь идет о генеральной средней µ.
Приведенные формулы касаются только одного параметра – среднего значения. Но вся логика оценки не меняется относительно других параметров генеральной совокупности, кроме, пожалуй, асимметрии и эксцесса.
Дело в том, что значение генерального параметра для этих показателей известно – они равны нулю. Тогда формула этих показателей принимает несколько иной вид:
(21)
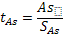
(22)
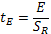
Полученное значение t сравнивают с табличным (приложение №2). Если оно меньше табличного, нет оснований считать, что полученное значение коэффициента существенно отличается от генерального параметра. Наоборот, если t > табличного значения, значит различие рассчитанного на выборке параметра существенно отличается от параметра генеральной совокупности, а следовательно обусловлено неслучайными воздействиями.
Результаты оценки параметров в генеральной совокупности нужно свести в таблицу вида:
Таблица 15.
Интервальная оценка параметров генеральной совокупности.
| Характеристика выборки | Ошибка характеристики выборки | Интервальная оценка параметра | Показатель точности оценки |
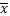
| |||
| 𝔖 | |||
| V | |||
| As | |||
| E |
Полученные результаты по интервальной оценке необходимо сопроводить соответствующими комментариями.
Используемый в таблице 15 показатель точности рассчитывается по формуле
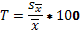
По величине этого показателя судят о степени отклонения выборочной характеристики от генерального параметра. Показатель точности считается приемлемым, если он лежит в пределах 5%.
4. Оценка соответствия эмпирического распределения теоретическому.
Оценка полученных рядов распределения по диаметру и по высоте с точки зрения их соответствия теоретическому распределению производится по так называемым критериям согласия. В контрольной работе используются два из них: критерий Колмогорова λ(лямбда) и критерий Пирсона 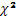 (хи-квадрат).
(хи-квадрат).
Первый критерий относительно прост, не требует использования характеристик выборочной совокупности и поэтому называется непараметрическим.
Расчет теоретических частот нормального распределения
Таблица 16.
| № | Классовая варианта
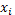
| Частота
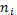
| Нормированное отклонение
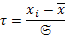
| ƒ(ί) (Табличн.) т.3 прил. | Теорет. частота
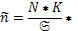 ƒ(ί) ƒ(ί)
|
| 50*4 | |||||
(1)
В формуле: k – величина интервала.
ƒ(ί) – из колонки 5.
Критерий λ рассчитывается по формуле:
(23)
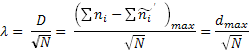
где: D – максимальная разность между эмперическими и теоретическими накопленными частотами в ВР.
Таблица 17.
Расчет критерия λ.
| № | Классовая варианта.
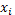
| Частоты. | Накопленные частоты. | Разница. | ||
эмп.
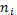
| теор.
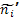
| 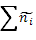 эмп. эмп.
| 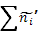 теор. теор.
| 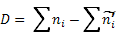
| ||
В шестой колонке находят класс, в котором разница между накопленными частотами максимальна. Подставляют его в формулу 23 и получают соответствующее значение λ.
Разница между накопленными эмпирическими и теоретическими частотами оцениваются по трем уровням доверительной вероятности: 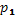 = 0,95,
= 0,95, 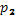 = 0,99,
= 0,99, 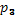 = 0,999. Этим уровням соответствуют значения λ: 1,36;. 1,63; 1,95.
= 0,999. Этим уровням соответствуют значения λ: 1,36;. 1,63; 1,95.
Расхождение частот признаются случайными, а следовательно, соответствующим теоретической частоте, если значение λ не превосходит своего критического значения при принятом уровне доверительной вероятности (таблица №4 приложений).
Критерий χ 2 аналогичен по структуре формуле дисперсии. То есть χ 2 – это относительная сумма квадратов отклонений эмпирических частот от теоретических:
(24)
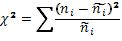
где: 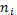 – эмпирическая частота.
– эмпирическая частота.
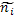 – теоретическая частота. (см. таблицу 17)
– теоретическая частота. (см. таблицу 17)
Смысл оценки состоит в том, что чем в меньшей степени эмпирические частоты отклоняются от теоретических, тем с большей вероятностью можно говорить о степени соответствия эмпирического распределения теоретическому.
Таблица 18.
Расчет критерия χ 2.
| № | Классовая варианта.
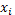
| Частоты. | Разность.
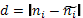
| Квадрат диаметра. d2 | χ 2 | |
эмп.
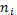
| теор.
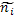
| |||||
Оценка степени соответствия производится по сумме значений колонки 7.
По таблице №4 приложений для соответствующего уровня доверительной вероятности и по числу степеней свободы вариационного ряда выбирает табличное значение (χ2). Если табличное (χ2) меньше фактического, то признаётся соответствие эмпирического и теоретического распределений. Число степеней свободы рассчитывается от количества классов минус 3 (m = 5 – 3= 2). При составлении таблицы 18 следует иметь в виду, что при вычислении χ2 частоты крайних классов ВР не должны быть менее 5.
Раздел 5. Расчет показателей связи в выборочной совокупности и их оценка.
В разбираемом нами примере были исследованы два признака: диаметр и высота. Получены статистические характеристики их ВР. На их основе можно приступить к количественной оценке связи между этими признаками. Сделать это можно двумя методами: используя корреляционный анализ или связанный с ним регрессионный анализ. В рамках контрольной работы выполняется оба вида анализа связи.
Корреляционный анализ начинают с построения так называемой корреляционной решетки – такой таблицы, в которой сопряжены два изучаемых признака в виде уже известных ВР.
Таблица 19.
| Корреляционная решетка. | ||||||||
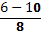
| 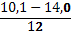
| 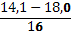
| 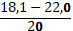
| 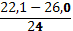
| 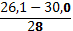
| 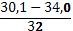
| ||
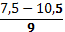
|
 3 3
|
 2 2
| ||||||
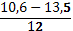
|
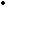 1 1
|
 2 2
|
 1 1
| |||||
|
 3 3
|
 2 2
|
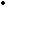 1 1
| |||||
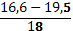
|
 1 1
|
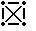 10 10
|
 4 4
| |||||
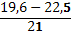
|
 3 3
|
 4 4
|
 5 5
|
 2 2
| ||||
|
 2 2
|
 1 1
|
 1 1
|
 1 1
| ||||
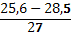
|
 1 1
| |||||||
| nx | ||||||||
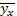
| 9,75 | 13,12 | 17,12 | 19,91 | 21,50 | 22,0 | 25,5 |
Характер распределения частот по сопряженным вариационным рядам уже позволяет сделать определенные выводы о наличии связи. Диагональное распределение частот от меньших значений вариант к большим по обоим ВР дает первую характеристику связи, которая называется направленностью. В данном случае она положительная: увеличению диаметров соответствует увеличение частот. Кроме того, распределение частот по клеткам корреляционной решетки вскрывает смысл корреляционного анализа. Он устанавливает зависимость средних значений одного варьирующего признака (высоты в данном случае) от фиксированных значений другого (диаметра).
Следующая характеристика связи между изучаемыми предметами – ее теснота. Теснота связи характеризуется числовым значением коэффициента корреляции:
(25)
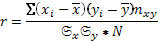
где: r – коэффициент корреляции.
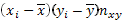 – произведение отклонений классовых вариант по диаметру и по высоте с учетом частоты по каждой клетки решетки.
– произведение отклонений классовых вариант по диаметру и по высоте с учетом частоты по каждой клетки решетки.
Величины коэффициента корреляции лежит в пределах -1 - +1. Знак перед r характеризует направленность связи. Абсолютная величина r показывает тесноту или силу взаимосвязи признаков. До 0,3 – связь практически отсутствует, от 0,3 до 0,5 – связь слабая, 0,5-0,7 – средняя, 0,7-0,9 – сильная. Свыше 0,9 – практически функциональная.
Форма связи между исследуемыми признаками, кроме ее визуальной оценки по корреляционной решетке, может быть охарактеризована более определенно по значению так называемого коэффициента криволинейности.
(26)
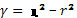
где: 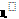 - корреляционное отношение.
- корреляционное отношение.
r – коэффициент корреляции.
Корреляционное отношение – аналог коэффициента корреляции, причем более универсальный: применим для любой формы связи. Рассчитывается по формуле:
(27)
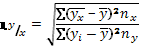
где: 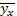 - частное среднее значение высоты по классам x (диаметр) с учетом суммарной частоты класса (
- частное среднее значение высоты по классам x (диаметр) с учетом суммарной частоты класса (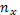 ) в корреляционной решетке.
) в корреляционной решетке.
Символ 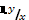 обозначает оценку связи y по x, то есть высоты в зависимости от диаметра, на что указывает индекс. По существу корреляционное отношение устанавливает долю частной дисперсии по y (высоте) в общей дисперсии.
обозначает оценку связи y по x, то есть высоты в зависимости от диаметра, на что указывает индекс. По существу корреляционное отношение устанавливает долю частной дисперсии по y (высоте) в общей дисперсии.
Ошибка коэффициента криволинейности рассчитывается по формуле:
(28)
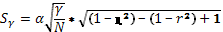
Вывод о форме связи делается на основании нулевой гипотезы (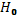 ) в предположении, что (
) в предположении, что (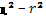 ) = 0, то есть связь прямолинейна.
) = 0, то есть связь прямолинейна.
(29)
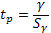
Тогда при 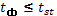 нулевая гипотеза принимается, то есть форма связи близка к прямолинейной. При
нулевая гипотеза принимается, то есть форма связи близка к прямолинейной. При 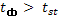 нулевая гипотеза отвергается, связь является криволинейной.
нулевая гипотеза отвергается, связь является криволинейной.
Доверительная оценка коэффициента корреляции производится по критерию Стьюдента:
(30)
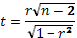
Предварительно следует рассчитать ошибку r:
(31)
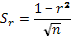
Нулевая гипотеза отвергается, если 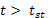 (для степени свободы n-2) при принятом уровне доверительной вероятности.
(для степени свободы n-2) при принятом уровне доверительной вероятности.
Доверительная оценка корреляционного отношения производится точно так же, только вместо r в формуле стоит ɳ.
Интервальная оценка как коэффициента корреляции, так и корреляционного отношения производится по формулам:
(32)
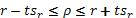
Таким образом, в рамках корреляционного анализа получены три характеристики связи: теснота, форма и направленность. В КР следует более тщательно отнестись к понятию «теснота». В общем плане – это степень сопряженного варьирования признаков. Однако, общее поле варьирования двух признаков включает в себя точки, отражающие разную степень зависимости двух признаков, в том числе такие значения зависимого признака (высота) которые лишь формально связаны с диаметрами, а на самом деле определяются суммарным влиянием других не учитываемых в опыте факторов. Отсюда следует, что коэффициент корреляции в той или иной степени преувеличивает оценку тесноты связи. Для того, чтобы исключить влияние случайных факторов(возможно, просто не учитываемых) на величину зависимого признака рассчитывается так называемый коэффициент детерминации.
d= r2
Значение d показывает долю значений признака, величина которых определяется преимущественно влиянием изменчивости диаметра. Например, если d=0,67, то это значит, что для 67% объема зависимого признака изменчивость определяется преимущественно изменчивостью факторного признака.
5. Регрессионный анализ.
В рамках регрессионного анализа, дополнительно характеристикам связи, полученным в корреляционном анализе, разработан способ оценки, который показывает на сколько изменяется, в среднем, зависимый признак при изменении независимого на одну единицу.
В корреляционном анализе установлена форма связи между признаками. Для установленной формы выбирают соответствующее уравнение общего вида. Допустим, что это уравнение прямой: y= a + bx.
В регресионом анализе исследуемые признаки подразделяют на результативный признак (признак-функцию) и факторный признак (признак аргумент). В нашем случае результативный признак – это высота (y), а факторный - диаметер(x).
Графический способ отражения связи.
По определению регрессия устанавливает соотношение между средними значениями результативного признака и фиксированными значениями факторного. По данным корреляционной решетки строим соответствующую линию
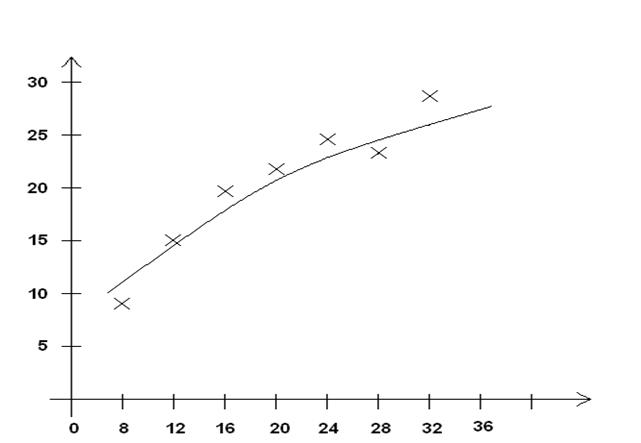
Рис. Линия регрессии, эмпирическая.
Способ заключается в том, что «на глаз» производится «усреднение» точек разброса эмпирической линии. Усредненные точки соединяются плавной линией, в результате чего получается выровненная линия регрессии. Ее можно считать первым приближением к теоретической кривой, рассчитываемой аналитическими методами.
Способ скользящей средней.
Способ осуществляется следующим образом. Берутся три или более последовательных значений переменной (результативные): y1 + y2 + y3, рассчитывается 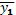 для x2 (факультативного), далее находят среднее по сумме y2 + y3+y4. Это будет
для x2 (факультативного), далее находят среднее по сумме y2 + y3+y4. Это будет 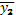 по x3; и т.д.
по x3; и т.д.
Таким образом, среднее из соседних значений будет более точно отражать общую линию связи.
Способ наименьших квадратов.
Этот способ дает наиболее точную оценку связи. Он основан на требовании минимизации суммы квадратов отклонений от средней, т.е 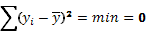 . Практически, в рамках контрольной работы, он реализуется следующим образом.
. Практически, в рамках контрольной работы, он реализуется следующим образом.
Каждая клетка корреляционной решетки содержит эмпирическую информацию о численном соотношении двух признаков (x – диаметр, y – высота), а также о количестве деревьев принадлежащих этому соотношению. То есть, по уже выбранному ранее общему виду уравнения связи можно построить столько эмпирических уравнений, сколько имеется заполненных клеток в корреляционной решетке. Например, из таблицы 19 для значений зависимого признака (x, y) соответственно 9 и 12(три и одно дерево в клетке), используя общий вид прямолинейной зависимости получаем:
(9=a+b*8)3
Далее таким же образом
(12=a+b*8)1
(15=a+b*12)3, и т.д.
Суммируя почленно эмпирические уравнения получаем в общем виде следующее уравнение:
(33)
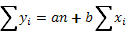
Это первое уравнение системы, решая которую мы получим значения а и b, которые, собственно, и определят зависимость двух исследуемых признаков.
Второе уравнение получается после умножения каждого предыдущего уравнения на числовое значение независимой переменной (коэффициент при b).
Продолжая рассматривать наш пример, получим:
[(9=a+b*8)3]8
[(12=a+b*8)1]8
[(15=a+b*12)3]12 и т.д.
Суммируя почленно получим второе уравнение системы, общий вид которого таков:
(34)
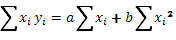
Таким образом, построив два уравнения с двумя неизвестными и решая их как систему, найдем значения этих неизвестных
(35)
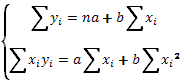
Тот же самый результат можно получить, прибегнув к математической формализации требования минимизации функции
(36)
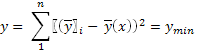
Минимум функции достигается, как известно, после приравнивания к нулю её первой производной.
Уравнение (36) изменяем в развернутом виде
(37)
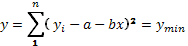
Находим частные производные функции y последовательно по a и b и приравниваем их к нулю.
(38)
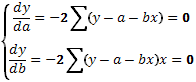
После несложных преобразований получаем последовательно:
(39)
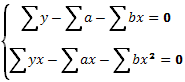
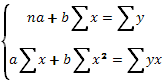
Таким образом, мы получим ту же систему нормальных уравнений, но несколько иным путем. Значения неизвестных из этой системы равны:
(40)
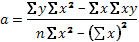
(41)
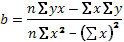
Для расчета этих же коэффициентов иногда удобно использовать следующие рабочие формулы:
(42)
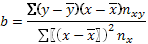
(43)
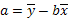
Подставляя рассчитанные значения a и b в уравнение общего вида y=a+bx, получим эмпирическое уравнение связи двух признаков:
(44)
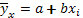
По уравнению рассчитываем значение 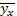 в зависимости от
в зависимости от 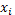 (значение классовых вариант в ВР по диаметру). Данные сводим в таблицу.
(значение классовых вариант в ВР по диаметру). Данные сводим в таблицу.
Таблица выровненных значений f(x).
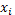
| x | |||||||
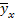
| 9,75 | 13,12 | 17,12 | 19,91 | 21,50 | 22,0 | 25,5 |
По приведенной таблице строим график установленной зависимости (формула). Следует совместить с эмпирической ломанной. 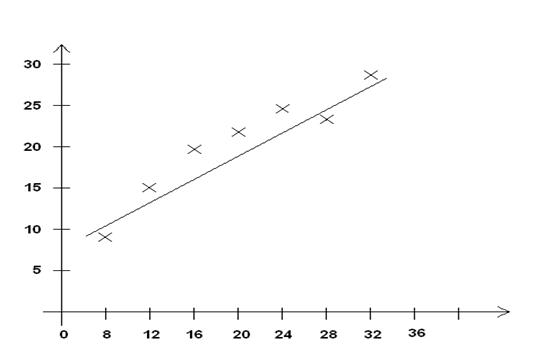
Рис. Эмпирическая линия связи по МНК.
Оценка репрезентативности установленной связи.
Коэффициенты в уравнении регрессии являются производными от исследуемых выборочных случайных величин. Следовательно, они сами являются величинами случайными и для них так же актуален вопрос: насколько рассчитанные значения соответствуют гипотетическим значениям генеральной совокупности.
Так же как и в предыдущих случаях, связанных с оценкой параметров, нужно рассчитать ошибку коэффициента регрессии (b):
(45)
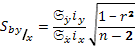
где – 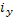 - величина интервала по y
- величина интервала по y
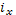 - величина интервала по x
- величина интервала по x
Достоверность коэффициента регрессии оценивается по критерию t. При
(46)
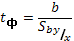
Знание ошибки экспериментального коэффициента регрессии, позволяет установить доверительную зону случайных отклонений линии выборочной регрессии в пределах, обеспечивающих присутствие линии генеральной регрессии с принятой вероятностью.
При этом нулевая гипотеза (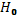 ) состоит в отрицании связи признаков, т.е. случай равенства нулю коэффициента регрессии.
) состоит в отрицании связи признаков, т.е. случай равенства нулю коэффициента регрессии.
Контрольная работа, выполненная по приведенной программе, является лишь одним из способов обработки исходной информации. В большинстве случаев как последовательность, так и методика анализа зависят от целевой установки экспериментатора, но, в любом случае, опыт обработки совокупности, приобретенный в данной работе будет несомненно полезен на любом этапе работы.
 2015-05-13
2015-05-13 2849
2849