Использование вероятностных моделей старения параметров РЭУ и элементов

Параметры РЭУ являются случайными функциями времени эксплуатации и хранения. В начальный момент, после изготовле­ния изделия, значения его параметров будут случайными вследст­вие технологических (производственных) погрешностей. Старение и износ проявляются в сравнительно медленном изменении пара­метров РЭУ, обычно в одну сторону. Как правило, процесс этот необратимый. Реализация этого процесса — монотонное измене­ние выходных параметров РЭУ во времени. Но скорость старения для различных экземпляров одного и того вида РЭУ обычно раз­лична и зависит от условий его использования и эксплуатации, конструктивного исполнения, и т.п. Время достижения парамет­ром его допустимой границы будет случайным.

Рассмотрим задачу определения закона распределения вре­мени достижения критических границ при постепенных измене­ниях параметров. Применение общей теории и методов случайных функций в этом случае затруднительно из-за сложности матема­тических выражений.

Для расчетов устойчивости параметров и надежности РЭУ по постепенных отказам выбирают математическую модель про­цесса старения. Реализации процессов старения, получаемые экс­периментально, в общем случае являются нелинейными. Для приближенных инженерных расчетов применяют линейную ап­проксимацию действительных кривых, т.е. предполагают линей­ные изменения параметра в каждом единичном экземпляре РЭУ в пределах среднего времени между двумя отсчетами.

В этом случае для параметра х, как функции времени t, можно записать

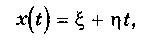(3.18)

где о, з —независимые случайные величины;

о= x(t = 0) —начальное значение параметра x(t); случайность

значения о определяется производственными причинами;

з —случайная скорость старения или износа, отражает

различие исходных свойств материалов и конструкций.

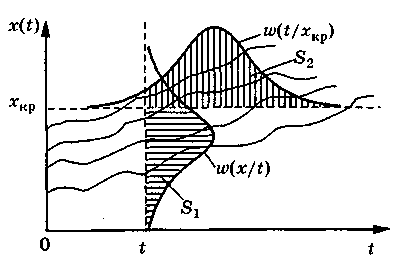
Рис.5.23. К вопросу о нахождении закона распределения времени достижения параметром критической границы

Сформулируем задачу таким образом. Известны законы рас­пределения величин о и з. Требуется найти закон распреде­ления времени t достижения параметром x(t) критической границы х_кр, что позволяет рассчитать вероятность того, что за время t параметр не достигнет критической границы, т.е. оценить вероятность, отсутствия за время t постепенного отказа по пара­метру x(t).

Для решения этой задачи выполним построения, показан­ные на рис.3.5.

В вертикальном сечении по t имеем распределениепараметра щ(x/t). В гори­зонтальном сечении по х_кр имеем плотность распреде­ления щ(t/x_кр) случайного времени достижения пара­метром x(t) критического уровня х_кр.

Из построений видно, что число реализаций, пересекающих границу х_кр для моментов времени, больших t, равно числу реализаций в сечении t при х <х_кр.

Следовательно, площади S₁ и S₂ равны между собой. В свою очередь можно записать:

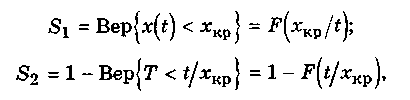
где Т — случайное время достижения параметром x(t) критической границы х_кр;

F(x_кp/t) — функция распределения параметра x(t), подсчи­танная для значения x(t) = х_кр в сечении t;

F(t/x_кp) — функция распределения времени достижения параметром x(t) критического уровня х_кр, под­считанная для значения t. Из равенства S₁ = S₂ получим

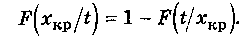
Отсюда

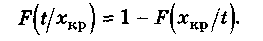
Из последнего выражения видно, что нужно определить значение функции распределения F(x/t) в точке x(t) = х_кр для сечения t.

Будем считать, что случайные величины о и з, входящие в функцию (3.18), подчиняются нормальным законам. Тогда сама функция x(t) также будет подчиняться нормаль ному закону с параметрами

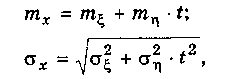
где у, т — знаки математического ожидания и среднего квадратического отклонения.

Выразим функцию распределения параметра x(t) через таб­личную функцию стандартного нормального распределения Ф

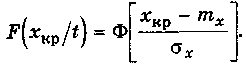
Функция распределения времени достижения критической границы:

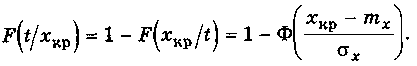
Вероятность того, что за время t параметр не достигнет кри­тического уровня x_кр определится как

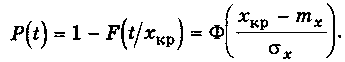
Это выражение может быть использовано и в задачах оцен­ки уровня параметрической надежности по параметру x(t).