Напомним, что под высказыванием мы понимаем предложение, о котором можно сказать одно из двух: истинно оно или ложно. Понятие предиката обобщает понятие высказывания. Теория предикатов представляет собой более тонкий инструмент, по сравнению с теорией высказываний. В настоящей главе рассматривается основные положения теории алгебры предикатов.
Определение 1 n- местным предикатом, определённым на множествах М1, М2,…,Мn, называется предложение, содержащее n переменных x1,x2,…,xn превращающееся в высказывание при подстановки вместо этих переменных любых конкретных элементов из множеств М1, М2,…,Мn соответственно.
Обозначать n -местные предикаты будем А (x1,x2,…,xn), причём переменные x1,x2,…,xn называются предметными.
Всякий n- местный предикат А (x1,x2,…,xn) определённый на множествах М1, М2,…,Мn есть функция от nаргументов, заданная на указанных множествах и принимающая значение 0(ложно) или 1(истинно).
Будем говорить, что n -местный предикат А (x1,x2,…,xn ) задан на множестве М, если x1,x2,…,xn принимают значения из М.
Примерами предикатов являются любые уравнения и неравенства из школьного курса математики.
Например, x+y>2, где x,y из R есть двухместный предикат заданный на множестве всех действительных чисел R.
Определение 2 Предикат А (x1,x2,…,xn) заданный на множествах
М1, М2,…,Мn называется:
1. тождественно истинным, если при любой подстановке вместо переменных x1,x2,…,xn любых конкретных значений из множеств
М1, М2,…,Мn он превращается в истинное высказывание.
2. тождественно ложным, если при любой подстановке вместо переменных x1,x2,…,xn любых конкретных значений из множеств М1, М2,…,Мn соответственноон превращается в ложное высказывание.
3. выполнимым, если существует по крайней мере один набор значений переменных из М1, М2,…,Мn, при которых его значение истинно.
Обозначают: тождественно истинный – А (x1,x2,…,xn) ≡ 1; тождественно ложный – А (x1,x2,…,xn) ≡ 0.
Двухместный предикат x²+y²≥0, заданный на множестве R является тождественно истинным.
Одноместный предикат sinx>1, заданный на множестве R является тождественно ложным.
Примером выполнимого предиката заданного на множестве R является предикат x+y>z.
Определение 3 Множеством истинности предиката А (x1,x2,…,xn) заданного на множествах М1, М2,…,Мn называется совокупность всех упорядоченных наборов (a1,a2,…,an), где aiÎМi, i=1,2,…,n при которых А(a1,a2,…,an) =1.
Множество истинности предиката А (x1,x2,…,xn) мы будем обозначать NA.
Пусть A(x)=(x²+3x-4=0) – одноместный предикат, заданный на множестве R. Ясно, что NA={1,-4}. Однако, если данный предикат задан на множестве натуральных чисел, то его множество истинности N′A={1}.
Пусть x²+y²=4 – двухместный предикат, заданный на множестве действительных чисел R. Тогда множеством истинности его являются множества всех таких пар действительных чисел, которые являются координатами точек плоскости, лежащих на окружности с центром в начале координат и радиусом 2.
Непосредственно из определения 2 следует справедливость следующего утверждения.
Пусть А (x1,x2,…,xn)n -местный предикат, заданный на множествах
М1, М2,…,Мn тогда справедливы следующие утверждения:
1. А (x1,x2,…,xn) является тождественно истинным тогда и только тогда, когда NA= М1× М2×…×Мn;
2. А (x1,x2,…,xn) является тождественноложным тогда и только тогда, когда NA=Ø;
3. А (x1,x2,…,xn) является выполнимым тогда и только тогда, когда NA≠Ø;
Определение 4 Два n -местных предиката А(x1,x2,…,xn) и В(x1,x2,…,xn) заданных на одних и тех же множествах М1, М2,…,Мn называются равносильными, если для любых наборов переменных (a1,a2,…,an), где aiÎМi, i=1,2,…,n они принимают одинаковые логические значения.
Непосредственно из данного определения следует, что предикаты
А(x1,x2,…,xn) и В(x1,x2,…,xn) равносильны тогда и только тогда, когда их множества истинности совпадают, то есть NA=NВ.
Тот факт, что предикаты А(x1,x2,…,xn ) и В(x1,x2,…,xn ) равносильны будем обозначать так: A=B.
Определение 5 Предикат А(x1,x2,…,xn) определённый на множествах М1, М2,…,Мn называется следствием предиката В(x 1, x 2,…, x n)определённом над теми же множествами, если он принимает истинные значения на всех тех наборах значений переменных, на которых истинно значение предиката А(x1,x2,…,xn).
Другими словами можно сказать, что предикат А(x1,x2,…,xn) является следствием предиката В(x1,x2,…,xn) тогда и только тогда, когда NВ Í NA.
Пусть А1(х)=х 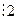 (x делится на 2) А2(х)= х
(x делится на 2) А2(х)= х 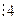 (x делится на 4) два одноместных предиката заданных на множестве натуральных чисел. Ясно, что предикат А1 является следствием предиката А2.
(x делится на 4) два одноместных предиката заданных на множестве натуральных чисел. Ясно, что предикат А1 является следствием предиката А2.
Так как любой предикат при фиксированных значениях переменных превращается в высказывание, то над ними можно проделывать те же логические операции, что и над высказываниями.
Определение 6 Отрицанием n-местного предиката А (x1,x2,…,xn) определённого на множествах М1, М2,…,Мn называется n -местный предикат, определённый на тех же множествах, обозначаемый 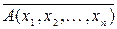 , значение которого истинно при всех тех значениях переменных, при которых значение предиката ложно.
, значение которого истинно при всех тех значениях переменных, при которых значение предиката ложно.
Например, отрицанием двухместного предиката x+y>2, определённого на множестве R является предикат x+y<2, определённый на том же множестве R.
Теорема 1 Пусть 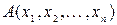 - n-местный предикат, определённый на множествах М1, М2,…,Мn. Тогда справедливо следующее тождество:
- n-местный предикат, определённый на множествах М1, М2,…,Мn. Тогда справедливо следующее тождество:
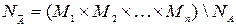 .
.
Доказательство Пусть 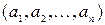 - произвольный набор переменных из
- произвольный набор переменных из 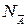 . Тогда
. Тогда 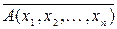 =1. Это возможно только тогда, когда
=1. Это возможно только тогда, когда 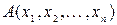 =0. А это значит, что
=0. А это значит, что
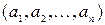
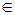
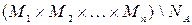 .
.
Отсюда следует справедливость указанного тождества. Непосредственно из данной теоремы следует:
Следствие Отрицание предиката будет тождественно истинным тогда и только тогда, когда исходный предикат тождественно ложен.
Определение 7 Конъюкцией n- местных предикатов 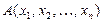 и
и 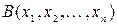 , определённых на множествах
, определённых на множествах 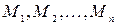 называется n-местный предикат, определённый на тех же множествах, обозначаемый
называется n-местный предикат, определённый на тех же множествах, обозначаемый 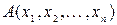 ·
· 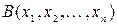 , значение которого истинно при тех и только тех наборах переменных, при которых истинно значение исходных предикатов.
, значение которого истинно при тех и только тех наборах переменных, при которых истинно значение исходных предикатов.
Теорема 2 Пусть 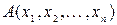 и
и 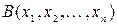 два n-местных предиката определённые на множествах
два n-местных предиката определённые на множествах 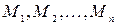 . Тогда справедливо следующее тождество:
. Тогда справедливо следующее тождество: 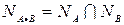 .
.
Доказательство Пусть 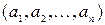 - произвольный набор переменных из
- произвольный набор переменных из 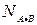 , тогда
, тогда 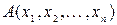 ·
· 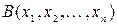 =1. Это возможно только тогда, когда одновременно
=1. Это возможно только тогда, когда одновременно 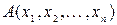 =1 и
=1 и 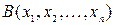 =1. А это значит, что
=1. А это значит, что 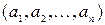
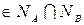 .Теорема доказана.
.Теорема доказана.
Непосредственно из данной теоремы следует:
Следствие Конъюнкция двух предикатов тождественно истинна тогда и только тогда, когда оба данных предиката тождественно истинны.
Теорема 2 используется в школьном курсе математики при решении систем уравнений и неравенств. Например, требуется решить систему неравенств 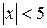 , x≥3. Для этого нужно найти множество истинности предиката(
, x≥3. Для этого нужно найти множество истинности предиката(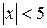 )· (x≥3), определённого на множестве R.Используя теорему 2 получаем:
)· (x≥3), определённого на множестве R.Используя теорему 2 получаем:
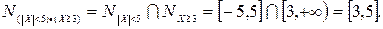
Определение 8 Дизъюнкцией n-местных предикатов A(x1, x2, …, xn) и B(x1, x2, …, xn), определенных на множествах M1, M2, …, Mn называется n-местный предикат, определенный на этих множествах, обозначенный
A(x1, x2, …, xn) V B(x1, x2, …, xn), значение которого истинно при тех и только тех наборов переменных, при которых истинно значение по меньшей мере одного из исходных предикатов.
Теорема 3 Пусть A(x1, x2, …, xn) и B(x1, x2, …, xn) два n-местных предиката, определенные на множествах M1,M2, …,Mn. Тогда справедливо следующее тождество NAVB = NA U NB.
Доказательство Пусть (a1,a2, …,an) – произвольный набор переменных из NAVB. Тогда A(x1, x2, …, xn) V B(x1, x2, …, xn) = 1. Это возможно только тогда, когда или A(x1, x2, …, xn)=1 или B(x1, x2, …, xn)=1. А это значит, что (a1 a2, …,an)Î NA U NB. Теорема доказана.
Следствие Дизъюнкция двух предикатов тождественно ложна тогда и только тогда, когда оба данных предиката тождественно ложны.
Теорема 4 Пусть A(x1, x2, …, xn), B(x1, x2, …, xn) и C(x1, x2, …, xn) –
n-местные предикаты, определенные на множествах M1,M2,…,Mn, тогда справедливы следующие равносильности:
A·B=B·A, AVB=BVA, A·(B·C)=(A·B)·C, AV(BVC)=(AVB)VC, A·(BVC)=A·BVA·C, AVB·C=(AVB)·(AVC), 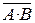 =
= 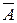 V
V 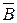 ,
, 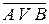 =
= 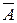 ·
· 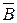 .
.
Доказательство Докажем справедливость следующей равносильности 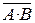 =
= 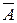 V
V 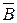 . Для этого нужно доказать справедливость следующего тождества N
. Для этого нужно доказать справедливость следующего тождества N 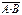 = N
= N 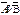 . Действительно, пусть (a1,a2,…,an) – произвольный набор переменных из N
. Действительно, пусть (a1,a2,…,an) – произвольный набор переменных из N 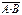 . Тогда
. Тогда 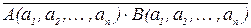 =1. Отсюда получаем, что A(a1,a2,…,an) B(a1,a2,…,an)=0. Это возможно только в том случае, когда либо A(a1, a2, …, an)=0, либо B(a1, a2, …, an)=0. А это значит, что либо
=1. Отсюда получаем, что A(a1,a2,…,an) B(a1,a2,…,an)=0. Это возможно только в том случае, когда либо A(a1, a2, …, an)=0, либо B(a1, a2, …, an)=0. А это значит, что либо 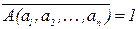 , либо
, либо 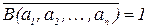 . Следовательно, (a1,a2,…,an) Î N
. Следовательно, (a1,a2,…,an) Î N 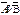 . Итак, N
. Итак, N 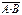 = N
= N 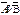 . Отсюда
. Отсюда 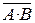 =
= 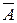 V
V 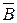 . Аналогичным образом можно доказать справедливость других равносильностей. Теорема доказана.
. Аналогичным образом можно доказать справедливость других равносильностей. Теорема доказана.
Определение 9 Пусть A(x1,x2,…,xn) и B(x1,x2,…,xn) n- местные предикаты на множествах M1,M2,…,Mn. Их импликацией называется предикат, определенный на тех же множествах, обозначаемый A(x1, x2, …, xn) => B(x1, x2, …, xn), значение которого ложно только при тех наборах переменных, при которых значение предиката A истинно, а B – ложно. Предикат A называется посылкой и B – заключение.
Непосредственно из определения следует, что импликация двух предикатов, зависящих от одних и тех же переменных, есть тождественно истинный предикат тогда и только тогда, когда ее заключение является следствием посылки.
Определение 10 Эквивалентность двух n- местных предикатов A(x1, x2, …, xn) и B(x1, x2, …, xn), определенных на множествах M1, M2, …, Mn,, называется n- местный предикат, определенный на тех же множествах, обозначаемый A(x1, x2, …, xn) <=> B(x1, x2, …, xn), значение которого истинно при всех тех наборах переменных, при которых предикаты A и B принимают одинаковые логические значения.
Непосредственно из определения 10 следует, что эквивалентность двух предикатов, зависящих от одних и тех же переменных, есть тождественно истинный предикат тогда и только тогда, когда они равносильны.
В следующей теореме доказаны важные равносильности, выражающие одни логические операции над предикатами через другие.
Теорема 5 Пусть A(x1, x2, …, xn) и B(x1, x2, …, xn) n-местные предикаты, определенные на множествах M1,M2, …,Mn. Тогда справедливы следующие равносильности:
A=>B= 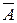 VB, A∙B=
VB, A∙B= 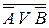 , A<=>B=(A=>B)∙(B=>A).
, A<=>B=(A=>B)∙(B=>A).
Доказательство Докажем справедливость следующей равносильности A<=>B=(A=>B)∙(B=>A). Для этого нужно доказать справедливость следующего тождества NA<=>B=N(A=>B)∙(B=>A). Пусть (a1,a2, …,an) – произвольный набор из NA<=>B. Отсюда следует, что A(a1,a2, …,an)<=>B(a1 a2,… …,an)=1. Это возможно только в том случае, когда либо значения A(a1,a2,.. …,an) и B(a1,a2, …,an) истинны, либо ложны одновременно. Но в любом из этих случаев значение (A(a1, a2, …, an)=>B(a1, a2, …, an)) (B(a1,a2, …, …an)=>A(a1, a2, …, an))=1, т.е. (a1, a2, …, an)Î N(A=>B)∙(B=>A) . Итак, требуемое тождество доказано. Отсюда следует справедливость отмеченной выше равносильности. Остальные равносильности доказываются аналогично. Теорема доказана.
Операции отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность определяются аналогично как для предикатов, так и для высказываний. Однако в теории предикатов существуют операции, для которых нет аналогов в теории высказываний. Такими операциями над предикатами являются две кванторные операции – квантор общности и квантор существования. Известно, что если в одноместном предикате зафиксировать значение переменной, то мы получим высказывание.
Имеется еще один способ. Он основан на применении к предикату операций связывания квантором общности или квантором существования. Такие операции ставят в соответствие одноместному предикату высказывание, значение которого зависит от строения исходного предиката.
Определение 11 Пусть A(x) – одноместный предикат, определенный на множестве M. Обозначим через 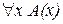 высказывание, которое читается: «для всякого x из M справедливо A(x)», данное высказывание истинно только в том случае, когда предикат A(x) тождественно истинный.
высказывание, которое читается: «для всякого x из M справедливо A(x)», данное высказывание истинно только в том случае, когда предикат A(x) тождественно истинный.
Символ 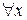 называется квантором общности по переменной x.
называется квантором общности по переменной x.
Например, пусть A(x)=(x2 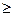 0) определенный на множестве R. Тогда
0) определенный на множестве R. Тогда 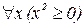 – истинное высказывание, которое читается: «квадрат любого действительно числа неотрицателен». Пусть A(x)=(x>2). Тогда
– истинное высказывание, которое читается: «квадрат любого действительно числа неотрицателен». Пусть A(x)=(x>2). Тогда 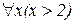 – ложное высказывание, которое читается: «любое действительное число больше 2».
– ложное высказывание, которое читается: «любое действительное число больше 2».
Следующая теорема показывает, что квантор общности можно рассматривать как обобщение конъюнкции.
Теорема 6 Пусть A(x) – одноместный предикат, определенный на конечном множестве M={ a1,a2, …,an}, тогда 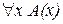 = A(a1)·A(a2)·…·A(an).
= A(a1)·A(a2)·…·A(an).
Доказательство Пусть 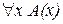 = 1, тогда A(x)≡1. Отсюда A(ai)=1 для любого aiÎM. Но тогда A(a1)·A(a2)·…·A(an)=1. Пусть
= 1, тогда A(x)≡1. Отсюда A(ai)=1 для любого aiÎM. Но тогда A(a1)·A(a2)·…·A(an)=1. Пусть 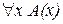 = 0, тогда
= 0, тогда
A(x)¹1. А это значит, что существует ai из M, что A(ai)=0. Но тогда A(a1)·A(a2)·…·A(an)=0. Теорема доказана.
Квантор общности можно применять и к многоместным предикатам. Однократное применение квантора к одной из n переменных n-местного предиката порождает (n-1) – местный предикат.
Пусть, например, мы имеем двухместный предикат A(x,y)=(x>y), определенный на множестве R. Тогда " x (x>y) задает одноместный предикат B(y), зависящий от переменной y. Определим тип этого предиката. Возьмем произвольное действительное число y0. Ясно B(y0)= " x(x>y0)=0. Следовательно, B(y) – тождественно ложный предикат.
Заметим, что к (n-1)- местному предикату " x1 A(x1,x2, …,xn) зависящему от переменных х1, x2,x3, …,xn можно снова применять операцию связывание квантором общности по одной из свободных переменных. В результате получится (n-2)- местный предикат и т.д.
Пусть, например, мы имеем двухместный предикат A(x,y)=(x+y>2), определенный на R. Тогда 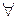 x " y (x+y>2) – ложное высказывание, которое читается: «сумма любых двух действительных чисел больше двух».
x " y (x+y>2) – ложное высказывание, которое читается: «сумма любых двух действительных чисел больше двух».
Определение 12 Пусть A(x) – одноместный предикат, определенный на множестве M. Обозначим 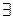 x A(x) – высказывание, которое читается: «существует x из M, что справедливо A(x)», данное высказывание ложно только в том случае, когда предикат A(x) тождественно ложный.
x A(x) – высказывание, которое читается: «существует x из M, что справедливо A(x)», данное высказывание ложно только в том случае, когда предикат A(x) тождественно ложный.
Символ 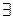 x называют квантором существования по переменной x.
x называют квантором существования по переменной x.
Например, пусть A(x)=(x2<0) определен на R. Тогда 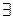 x (x2<0) – ложное высказывание, которое читается: «существует действительное число, квадрат которого меньше 0».
x (x2<0) – ложное высказывание, которое читается: «существует действительное число, квадрат которого меньше 0».
Следующая теорема показывает, что квантор существования можно рассматривать как обобщение дизъюнкции.
Теорема 7 Пусть A(x) – одноместный предикат, определенный на конечном множестве M={a1,a2, …,an}. Тогда 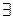 x A(x)=A(a1)VA(a2) V…VA(an).
x A(x)=A(a1)VA(a2) V…VA(an).
Доказательство Пусть 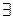 x A(x)=0. Тогда согласно определению 12 A(x) – тождественно ложный предикат, а значит A(ai)=0 для любого aiÎM, но тогда A(a1)VA(a2) V…VA(an)=0. Пусть
x A(x)=0. Тогда согласно определению 12 A(x) – тождественно ложный предикат, а значит A(ai)=0 для любого aiÎM, но тогда A(a1)VA(a2) V…VA(an)=0. Пусть 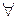 x A(x)=1. Тогда А(х) – не тождественно ложный предикат. А это значит, что найдется значение аi из М,что А(а i)=1. Но тогда А(а1)
x A(x)=1. Тогда А(х) – не тождественно ложный предикат. А это значит, что найдется значение аi из М,что А(а i)=1. Но тогда А(а1) 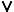 А(а2)
А(а2) 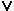 …
… 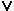 А(аn)=1. Теорема доказана.
А(аn)=1. Теорема доказана.
Квантор существования можно применять к многомерным предикатам. Однократное применение квантора к одной из n переменных а- мерного предиката порождает (n-1)- мерный предикат.
Пусть, например, мы имеем двухместный предикат А(х,у)=(х>у) определённый на множестве R. Тогда 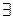 х(х>y) задает одноместный предикат В(у), зависящий от переменной у. Данный предикат будет тождественно истинным. Действительно, пусть у0 – произвольное фиксированное действительное число. Тогда В(у0)=
х(х>y) задает одноместный предикат В(у), зависящий от переменной у. Данный предикат будет тождественно истинным. Действительно, пусть у0 – произвольное фиксированное действительное число. Тогда В(у0)= 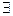 х(х>y0)=1.
х(х>y0)=1.
Заметим, что если в многомерном предикате все переменные связаны кванторами, то он будет высказыванием.
Пусть А(х,у)=(х+у>1) двухместный предикат определённый на множестве R.
Тогда из него связыванием переменных х и у можно получить восемь высказываний:
1. 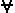 х
х 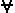 у(х+у>2) – “Для всяких действительных чисел х и у их сумма больше двух”.
у(х+у>2) – “Для всяких действительных чисел х и у их сумма больше двух”.
2. 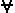 у
у 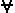 х(х+у>2) – “Для всяких действительных чисел у и х их сумма больше двух”.
х(х+у>2) – “Для всяких действительных чисел у и х их сумма больше двух”.
3.  х
х 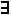 у(х+у>2) – “Существуют действительные числа х и у, сумма которых больше двух”.
у(х+у>2) – “Существуют действительные числа х и у, сумма которых больше двух”.
4. 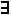 у
у 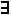 х(х+у>2) – “Существуют действительные числа у и х, сумма которых больше двух”.
х(х+у>2) – “Существуют действительные числа у и х, сумма которых больше двух”.
5. 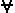 х
х 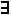 у(х+у>2) – “Для всякого действительного числа х существует действительное число у, что их сумма больше двух”.
у(х+у>2) – “Для всякого действительного числа х существует действительное число у, что их сумма больше двух”.
6. 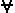 у
у 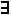 х(х+у>2) – “Для всякого действительного числа у существует
х(х+у>2) – “Для всякого действительного числа у существует
действительное число х, что их сумма больше двух”.
7. 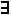 х
х 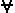 у (х+у>2) – “Существует действительное число х, что для всякого действительного числа у их сумма больше двух ”.
у (х+у>2) – “Существует действительное число х, что для всякого действительного числа у их сумма больше двух ”.
8. х (х+у>2) – “Существует действительное число у, что для всякого
действительного числа х их сумма больше двух ”.
Нужно заметить, что высказывания 1 и 2 оба ложны и имеют один и тот же смысл; высказывания 3 и 4 оба истины и имеют один и тот же смысл. Как видно, изменение порядка одноименных кванторов не влияет на смысл и значение истинности высказывания. Высказывание 5 истинно, а высказывание 8 ложно.
Высказывание 7 ложно, а высказывание 6 истинно. Как видно, изменение порядков разноименных кванторов приводит к изменению смысла и, возможно, значения истинности высказывания.
Понятие формулы алгебры логики предикатов определим индуктивно.
Вначале задается алфавит символов, из которых будут составляться формулы.
1. Предикатные переменные: x, y, z, xi, yi, zi (iÎN).
2. Нульместные предикатные переменные: А,В,С,Аi,Вi,Сi (iÎN).
3. n- мерные (n>=1) предикатные переменные:
А(…), В(…), А i(…), В i(…) (iÎN)
4. Символы логических операций:  ,
,  ,
, 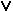 ,
, 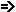 ,
, 
5. Кванторы: 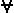 ,
, 
 2015-06-28
2015-06-28 307
307








