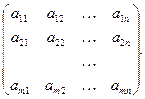Решение матричной игры в чистых стратегиях

Рассмотрим матричную игру с игроками P₁ и P₂ и платежной матрицей

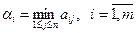Предполагая поведение игрока P₁ крайне осмысленным, необходимо считать, что игрок P₂ сыграет наилучшим для себя образом и на выбор игроком P₁ стратегии X_i выберет ту стратегию Y_j, при которой выигрыш игрока P₁ окажется минимальным. Обозначим минимальный среди выигрышей через α_i.

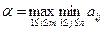
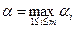
Продолжая действовать разумно, игрок P₁ должен выбрать ту стратегию, которая максимизирует показатель эффективности, т.е. для которой число α_i максимально.

Обозначим:, тогда. Число α называется нижней ценой игры в чистых стратегиях, а стратегия X_i0, которая максимизирует показатель эффективности α_i называется максиминной стратегией игрока P₁.

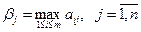Но так как игрок P₂ предполагает, что игрок P₁ играет наилучшим для себя образом, то выигрышем игрока P₁ будет максимальное из этих чисел, обозначим β_j:

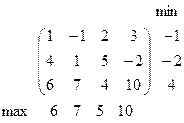
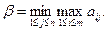
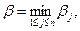Таким образом, для любой стратегии Y_j игрока P₂ наибольший его проигрыш равен β_j. В интересах игрока P₂ выбрать стратегию с минимальным показателем неэффективности. Наименьшее из чисел β_j обозначим β: тогда Число β называется верхней ценой игры в чистых стратегиях, а стратегия Y_j0, которая минимизирует показатель неэффективности β_j называется минимаксной стратегией игрока P₂.

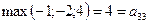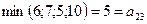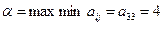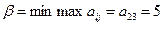-нижняя цена игры

-верхняя цена игры

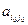
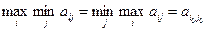X ₃ - максиминная стратегия, Y ₃ - минимаксная стратегия

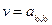
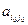Если, то элемент называется седловым элементом матрицы А. Если платежная матрица A имеет седловой элемент, то матричная игра имеет решение в чистых стратегиях, при этом оптимальной стратегий первого игрока является X_i0 чистая стратегия, а для второго – Y_j0 чистая стратегия, а цена игры.

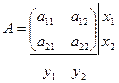Решение матричной игры 2´2 в смешанных стратегиях

Решить игру с платежной матрицей

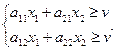Если X *=(x ₁; x ₂) – оптимальная стратегия первого игрока, то по определению решения матричной игры

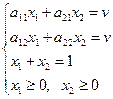Если игра с нулевой суммой, то

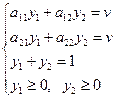Если Y *=(y ₁; y ₂) – оптимальная стратегия второго игрока Если игра с нулевой суммой, то

Решение игр с платежной матрицей 2´n

Алгоритм:

1) Через концы горизонтального отрезка [0; 1] провести два перпендикуляра к нему: левый и правый. Каждой точке отрезка [0; 1] будем ставить некоторую смешанную стратегию (x; 1- x).

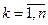2) На левом перпендикуляре от точки 0 отложить элементы (a ₁₁, …, a _{1 n}). На правом перпендикуляре от точки 1 отложить элементы (a ₂₁, …, a _{2 n}).

3) Соединить отрезками элементы a _{1 k} и a _{2 k} ().

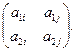4) Выделить нижнюю огибающую всех построенных отрезков, и найти максимальную точку (точки). Пусть точка является пересечением отрезков [ a _{1 i}; a _{2 i} ] и [ a _{1 j}; a _{2 j} ]. Тогда оптимальную стратегию можно найти при помощи матрицы

В матрицах mx2 тоже самое, только берётся верхняя огибающая и минимальная точка.