Визначення кількості реалізацій під час моделювання випадкових величин

Важливою задачею статистичної обробки результатів моделювання є задача точності отримання оцінок.

Для оцінки значення деякого параметра а за результатами моделювання Х_і слід брати величину 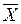, яка є функцією від усіх значень Х_і. Оскільки статистична оцінка 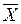також є випадковою величиною, то вона буде відрізнятися від а, тобто

,

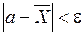де e – точність оцінки. Позначимо через а ймовірність того, що дана нерів­ність виконується

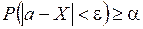. (2.33)

Вираз (2.33) використовується для визначення точності результатів статистичних випробовувань.

Нехай метою моделювання є оцінювання ймовірності настання деякої події А. Настання події А у кожній з N реалізацій моделі є випадковою величиною x. Вона набуває значення Х ₁ = 1 з ймовірністю р і Х ₂ = 0 з ймовірністю 1 –р. Математичне сподівання і дисперсію величини x визначаємо за формулами:

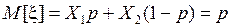; (2.34)

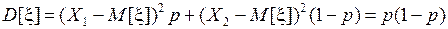. (2.35)

Для отримання оцінки р як частості настання події А за умови задання N реалізацій достатньо накопичувати величину m

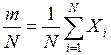, (2.36)

де Х_і – настання події А в і -тій реалізації. Тоді вибіркове математичне сподівання і дисперсію визначаємо за формулами (2.34) – (2.36). Отримаємо

.

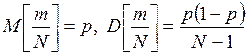Згідно з центральною граничною теоремою випадкова величина m / N має розподіл, який є близьким до нормального [4, 12].

Тому з таблиці нормального розподілу для кожного рівня достовірності 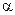знаходимо таку величину t_a, для якої точність обчислюватиметься за формулою

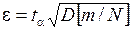(2.37)

Враховуючи у (2.37) значення дисперсії, отримаємо

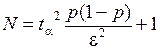. (2.38)

Якщо р = 1 або р = 0, то N = 1. Але оскільки ймовірність р є заздалегідь невідомою, то для визначення остаточної кількості реалізації проводять випробовування (N =50…100), оцінюють частість m / N і знайдену величину підставляють у формулу (2.38) замість р.

Визначення кількості реалізації для оцінки середнього значення випадкової величини здійснюється за таким алгоритмом. Нехай випадкова величина в і -й реалізації набуває значення Х_і. Вона має математичне сподівання m і дисперсію s ². За оцінку математичного сподівання m використовуємо середнє арифметичне

.

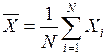Згідно з центральною граничною теоремою для великих значень N середнє арифметичне 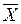буде мати нормальний розподіл з математичним сподіванням m і дисперсією 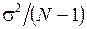. Отже, похибка оцінки визначається за формулою

.

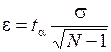Звідси знаходимо кількість реалізації

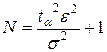. (2.39)

Оскільки дисперсія s² випадкової величини є невідомою, потрібно провести 50…100 випробовувань і знайти оцінку s². Отримане значення підставляємо у (2.39) для визначення необхідної кількості реалізації N.

Контрольні запитання та завдання

1. Розкрийте суть методу статистичних випробувань.

2. Охарактеризуйте генератори випадкових чисел, рівномірно розподілених в інтервалі (0, 1).

3. Наведіть алгоритми конгруентних методів генерування випадкових чисел.

4. Змоделюйте настання деякої елементарної події А, ймовірність появи якої в одному випробуванні дорівнює Р (А) = 0,4. Вважаємо що умови проведення кожного випробування одинакові і його можна повторити нескінченну кількість разів.

5. Змоделюйте настання групи несумісних подій А ₁, А ₂,..., А ₅, якщо відомі ймовірності їх настання Р (А ₁) = 0,3, Р (А ₂) = 0,2, Р (А ₃) = 0,1, Р (А ₄) = 0,15, Р (А ₅) = 0,25.

6. Змоделюйте настання складної (сумісної) події, що складається з двох залежних подій A і В з імовірностями Р (А) = 0,6; Р (B/Ā)=0,7.

7. Змоделюйте настання дискретної випадкової величини, яка приймає значення х ₁, х ₂,..., х ₁₀ з однаковою імовірністю Р = 0,1.

8. В чому полягає суть методу оберненої функції для моделювання випадкової величини Х, яка має функцію щільності f (x) і монотонно зростаючу функцію розподілу F (x)?

9. В чому полягає суть методу кусково-лінійної апроксимації для моделювання випадкової величини Х, яка має функцію щільності f (x)і монотонно зростаючу функцію розподілу F (x)?

10. Змоделюйте неперервну випадкову величину, яка має рівномірний розподіл в інтервалі [2,8].

11. Змоделюйте неперервну випадкову величину, яка має експоненціальний розподіл з параметром λ = 0,9.

12. Опишіть послідовність моделювання неперервного випадкового вектора?

13. Змоделюйте N = 15 реалізацій нормального випадкового вектора 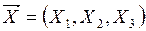з математичним сподіванням 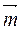= (5, –2, 0) та кореляційною матрицею

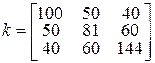
14. В чому полягає специфіка моделювання випадкових функцій?

15. Опишіть послідовність моделювання дискретних систем?

16. Спеціалізована операційна система приймає на обробку три класи завдань А, В і С з різним необхідним обсягом оперативної пам'яті. Імовірності появи завдань Р (А) = 0.5; Р (В) = 0.3; Р (С) = 0.2. В момент надходження завдання система може знаходитися в одному з двох станів: z ₁ – має вільні ресурси і може прийняти додаткові завдання; z ₂ – монополізована попередніми завданнями. Матриці перехідних імовірностей системи такі:

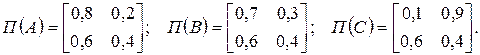
Вихідний сигнал – це стан системи в момент надходження чергового завдання. Змоделюйте роботу ОС при надходженні k = 20 завдань, якщо функціонування системи починається за відсутності завдань.

“Помилятися людині властиво, але

кінцево може запутати лише комп’ютер”

(п’ятий закон ненадійності)