Элементы теории вероятностей

Для математического описания различных явлений, например, теплового движения атомов или молекул, в статистической физике используют представления теории вероятностей. Теория вероятностей, в свою очередь, оперирует понятием случайного события.

Случайные события.

Случайным называется такое событие, которое при осуществлении заданных условий (т.е. при данном испытании) может как произойти, так и не произойти и для которого имеется определенная вероятность его наступления.

Для понимания смысла термина «случайное событие» совершенно не обязательно обращаться к гигантским совокупностям молекул или атомов. Случайные события – обычное явление в жизни.

Именно с такими событиями мы встречаемся, когда бросаем монету, кубик (кости), или, что гораздо менее приятно, когда на голову падает кирпич и т.д. Случайными событиями являются также результаты измерений координат и скоростей отдельных частиц.

Как уже отмечалось, непредсказуемым результат делает множество случайных и неконтролируемых факторов, которые могут повлиять на поведение интересующего нас объекта, хотя само движение этого объекта строго подчиняется законам механики.

Чтобы ввести понятие вероятности наступления какого-либо события, рассмотрим сосуд, в котором находится всего одна молекула, мысленно разделив объем сосуда на две части, и зададимся вопросом – где

находится молекула? Проведя большое число 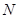наблюдений, получаем, что из

них 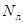раз частица оказывается в левой половине сосуда.

Тогда вероятность нахождения частицы в левой половине сосуда можно

определить как отношение “положительного” результата к полному числу

испытаний при достаточно большом их числе.

Наличие у случайного события определенной вероятности 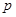его наступления проявляется в том, что при большом числе испытаний частота его наступления оказывается близкой к .

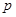Это частотное определение вероятности:

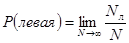(1.1)

Такое определение вероятности как предельного значения относительной частоты принадлежит немецкому математику Р. Мизесу.

Вероятность случайного события может быть определена как количественная мера ожидаемой возможности его появления.

Опыт или совокупность условий, в результате которых появляется то или иное событие, называется испытанием.

Если при данных условиях некоторое событие обязательно произойдет, то оно называется достоверным. Если какое-либо событие произойти не может, то его называют невозможным.

Рассмотрим для примера бросание кубика. Вероятность выпадения какого-либо числа 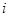от 1 до 6:

.

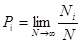В силу равновероятности выпадения любой грани, что определяется симметрией правильного куба, сделанного из однородного материала, имеем

.

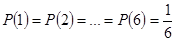Сумма вероятностей всех таких событий, т.е. выпадения какого-либо числа, равна единице. Т.о., мы приходим к понятию нормировки вероятности. Говорят, что вероятность нормирована на единицу, если

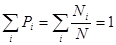. (1.2)

Иначе можно сказать, что выпадение при бросании кубика какого-либо числа от 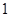до 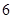включительно, есть достоверное событие.

В то же время ни при каком количестве испытаний на таком кубике не может выпасть число 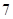. Это невозможное событие.

Достоверное и невозможное события можно рассматривать как предельные варианты случайных событий. Вероятность достоверного события равна единице, а невозможного – нулю.

Для молекулы, находящейся в сосуде объемом , можно рассмотреть вероятность того, что эта частица попадет в выделенный малый объем 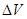, принадлежащий тому же сосуду. Для этого в течение длительного времени через равные временные промежутки 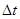определяем положение молекулы. Число проведенных наблюдений составит 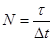. Пусть за всё время наблюдения частица проводит внутри малого объема 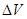время 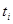, тогда число “положительных“ результатов будет равно .

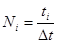Вероятность того, что частица будет обнаружена в объеме 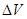, определяется как

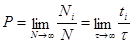(1.3)

Если время наблюдения достаточно велико, то время пребывания частицы в выделенном элементе объема 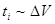, тогда вероятность наступления интересующего нас события

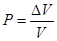. (1.4)

Теперь пусть положение частицы задается координатой 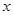. Если эта величина принимает дискретный ряд значений 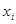( 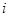=1,2,3,...), то вероятность того, что молекула находится в состоянии с координатой 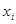, также определяется выражением (4.3), где 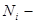число измерений, в которых для координаты частицы получено значение 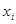, а 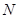- полное число измерений, 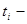время, которое частица проводит в состоянии .

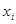Непрерывное распределение вероятности.

Если допустить теперь непрерывное изменение координаты, то бессмысленно говорить о вероятности нахождения частицы точно в точке с координатой 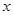. Действительно, непрерывная случайная величина 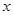имеет бесчисленное множество возможных значений (так называемое «несчетное множество»), сплошь заполняющих некоторый промежуток. Поэтому составить таблицу, в которой были бы перечислены все возможные значения такой случайной величины, невозможно. Кроме того, каждое отдельное значение непрерывной случайной величины обычно не обладает никакой отличной от нуля вероятностью, т.к. она имеет размерность нуль и в ней частица находится бесконечно малое время.

Правильно в этом случае определять вероятность того, что частица находится в интервале значений координаты от 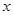до 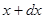. Различные области возможных значений случайной величины могут не быть одинаково вероятными, поэтому для непрерывно изменяющейся величины существует «распределение вероятностей». Время 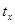, которое частица проводит в интервале 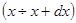пропорционально 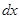, и тогда вероятность попадания частицы в этот интервал может быть записана как

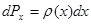. (1.5)

Здесь 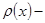коэффициент пропорциональности, дающий вероятность нахождения частицы в интервале единичной длины. Коэффициент 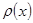называют плотностью вероятности.

Обратимся снова к частице, заключенной в объеме , и определим вероятность её попадания в объем 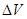, являющийся частью объема . По-прежнему

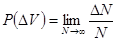. (1.6)

Определим плотность вероятности как

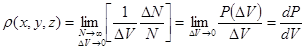. (1.7)

Или

.

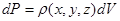Подход к нахождению вероятности обнаружения частицы посредством задания плотности вероятности является более универсальным, поскольку позволяет вычислить вероятность интересующего нас события и том случае, когда пространство, в котором заключена частицы неоднородно.

Если проведено 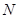измерений, то число измерений 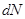, соответствующих попаданию частицы в бесконечно малый объем 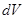(под 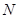в будущем будем понимать число частиц в рассматриваемом объеме), определяется как

,

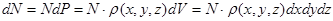а в конечный объем :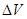

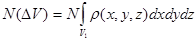
и вероятность обнаружить частицу в объеме :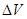

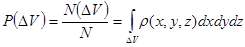. (1.8)

Условие нормировки для непрерывно изменяющихся величин имеет вид:

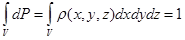. (1.9)

В заключение параграфа сделаем следующие важные замечания.

Конечно же, применение теории вероятностей было бы весьма затруднительно, если для определения вероятностей наступления событий требовалось бы на самом деле проводить серию соответствующих испытаний для определения предельных частот. В действительности вероятности определяются обычно не эмпирически, а либо на основании соображений симметрии (как в случае с игральным кубиком), либо вводятся a priori на основании какой-либо гипотезы, справедливость которой обосновывается всеми полученными теорией следствиями.

Одной из основных задач теории вероятностей является определение вероятности сложных событий по известным вероятностям простых событий. Наиболее просто такая задача решается, если возможность наступления какого-либо событие, никак не связана с появлением любого другого из возможных событий. Такие события называются статистически независимыми.

Простейшим примером таких событий опять-таки является выпадения какого-либо числа очков при последовательном бросании игральной кости (или при одновременном бросании нескольких костей).

2.2. Основные теоремы.

а). Теорема сложения вероятностей.

Пусть имеем дискретный набор случайных величин, характеризующих состояние системы. Назовем одно из возможных состояний системы 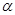, а другое – 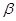. Если система не может одновременно находиться в состоянии 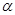и в состоянии 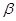, то мы имеем дело с взаимоисключающими событиям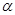и: или .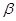

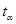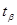Пусть времена их нахождения в этих состояниях равны и , соответственно. Тогда вероятность системе попасть в состояния либо 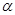, либо 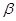есть:

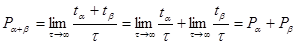. (1.10)

Это теорема сложения вероятностей для двух взаимоисключающих событий.

Примеры: бросаем кубик - ожидаем «5» или «6», молекула внутри объема .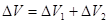

Исходя из этого, формируется условие нормировки вероятностей:

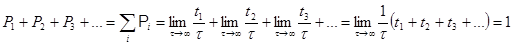, (1.11)

т.к. сумма по всем возможным состояниям, или по всем временам 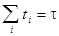, дает единицу.

Для непрерывного распределения переменной :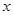

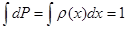. (1.12)

б). Теорема умножения вероятностей.

Рассмотрим две независимые физические системы 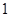, состояние которой характеризуются совокупностью величин 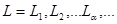и 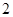, состояние которой характеризуются совокупностью величин 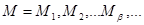, соответственно.

Системы называются статистически независимыми, если вероятность 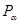нахождения системы 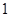в состоянии 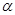со значением 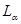никак не зависит от вероятности нахождения системы 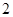в состоянии 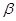со значением .

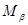Найдем вероятность того, что первая система находится в состоянии a, а вторая - в состоянии b:

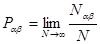(1.13)

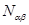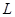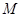где - число измерений, в которых параметры систем и одновременно принимают значения 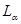и 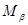, соответственно. Число измерений, когда система 1 находится в состоянии, характеризуемом значением 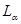: 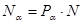. Однако лишь в некоторой доле этих измерений параметр 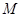системы 2 принимает значение 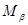. Нетрудно видеть, что: 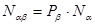. Тогда получаем теорему умножения вероятностей для статистически независимых систем:

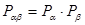(1.14)

Примеры:

1) бросаем два кубика (либо один кубик бросаем два раза), интересуемся вероятностью выпадения у одного “ 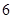”, а у второго - “ ”, тогда имеем: .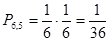

Если нам безразлично, на каком конкретно кубике выпадает одно из этих чисел, то вероятность такого

события: .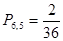

2) Одновременное попадание двух молекул в объем : .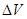

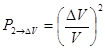2.3. Среднее значение случайной величины.

Как уже неоднократно подчеркивалось, особый интерес для описания макроскопических систем, образованных очень большим числом частиц, зачастую представляет не полный набор возможных значений интересующей нас величины и их вероятности, а её среднее значение.

Определим среднее значение случайной величины или, в пределе, математическое ожидание.

Пусть некоторая физическая величина 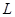принимает дискретный ряд значений 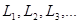с соответствующими вероятностями 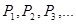их появления.

Среднее значение 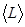физической величины 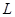определяется (подобно нахождению центра масс) как

,

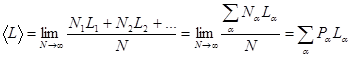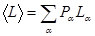. (1.15)

Среднее значение произвольной функции 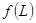равно

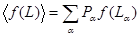. (1.16)

Для непрерывно изменяющихся величин (например, координаты 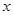) имеем

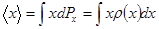, (1.17)

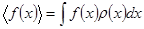, (1.17а)

где интегрирование проводится по всем возможным значениям .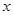

Рассмотрим некоторые свойства средних значений.

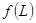1. Пусть и 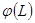- две различные функции случайной величины 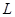. Тогда среднее значение суммы равно этих функций равно

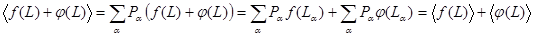. (1.18)

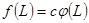1. Если , где 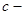постоянный множитель, то

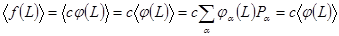. (1.19)

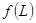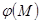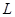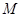1. Если и - функции аргументов и , соответственно, то

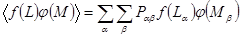. (1.20)

В том случае, когда переменные 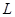и 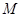описывают две статистически независимые системы,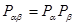

и тогда

.

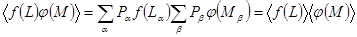3.4. Флуктуации.

При статистическом описании задачи возникает естественный вопрос, с какой точностью значение 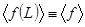характеризует наблюдаемые на опыте значения 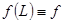? Совершенно очевидно, что величина может отклоняться от своего среднего значения и, в отдельных случаях, весьма значительно. Как уже отмечалось, мы рассматриваем поведение макроскопических систем, и рассматриваемые отклонения будут определяться коллективным поведением огромного числа частиц. Поэтому нас интересует мера отклонения среднего отклонения функции от своего среднего значения .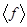

Среднее значение отклонения от своего среднег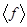о равно

,

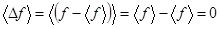и поэтому не может являться мерой среднего отклонения от своего среднего значения 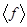. Равенство нулю 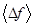связано с тем, что отклонения от своего среднего значения в одну и другую стороны при случайных отклонениях встречаются одинаково часто.

За меру среднего отклонения величины от 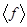выбирают обычно величину

,

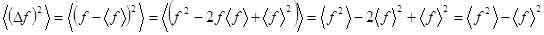называемую квадратичной флуктуацией величины .

Наряду с квадратичной флуктуацией для описания возможных отклонений параметров макроскопической системы от своих средних значений часто используют величину

,

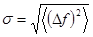называемую дисперсией, а также относительную квадратичную флуктуацию, определяемую как

.

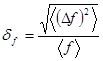Флуктуация – отклонение случайной величины от своего среднего значения. Она характеризует, как часто состояние системы отклоняется от своего среднего значения.