2017-11-01
733
Использование формул преобразования произведения двух синусов или косинусов, или синуса на косинус равных углов в сумму.
;
;
.
Пример 18. Найти 
.
Решение
.
Пример 19. Найти 
.
Решение
.
Решить самостоятельно
Найти
1) 
Ответ: 
;
2) 
Ответ: 
.
I Использование формул синуса и косинуса половинного аргумента
С помощью этих формул понижается степень функции, применяются они, когда в подынтегральном выражении находится синус или косинус в четной степени.
;
.
Пример 20. Найти 
.
Решение
.
Пример 21. Найти 
.
Решение
.
В этом примере, как вы видите, дважды применялась формула для понижения степени 
и 
.
Решить самостоятельно
Найти
1) 
Ответ: 
;
2) 
Ответ: 
.
III Использование формулы 
Эта формула используется, когда в подынтегральном выражении стоит синус или косинус в нечетной степени.
Пример 22. Найти 
.
Решение
Первый интеграл табличный, а второй находим способом подстановки:
Подставляем значения 
и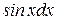 
во второй интеграл, оставляя первый без изменения, получим:
|
|
|
От новой переменной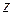 
возвращаемся к старой переменной
Решить самостоятельно
Найти
1) 
Ответ: 
.
IV Использование разных формул из тригонометрии
Пример 23. Найти 
.
Решение
.
При решении использованы формулы:
1) 
;
2) 
.
Третий способ – применение тригонометрических подстановок.
Интегралы, содержащие:
– решаются часто подстановкой 
;
– решаются часто подстановкой 
.
Пример 24. Найти 
.
Решение
Введем подстановку 
, так как 
, продифференцируем:
.
В подынтегральном выражении вместо 
и 
подставим найденные значения, получим:
.
Понижаем степень функции, применяя формулу :
.
Теперь выразим новую переменную 
через старую . Из подстановки имеем 
.
Остается подставить в полученный результат и упростить далее.
Упростим 
по формуле 
, получим:
.
Использованы знания обратных тригонометрических функций:
;
;
.
Подставляем значение , получаем ответ:
.
Пример 25. Найти 
.
Решение
Вводим подстановку , тогда 
, продифференцируем подстановку:
;
.
Подставим в подынтегральное выражение вместо 
, и полученные значения.
.
Находим интеграл методом подстановки:
.
Подставляем в полученный интеграл:
.
Выразим 
через старую переменную . Из подстановки 
имеем: 
, тогда 
.
Зная, что 
, из этой формулы найдем 
:
.
Имеем:
.
Значение подставим в полученный конечный результат.
.
Решить самостоятельно
Найти
1) 
Ответ: 
.
Четвертый способ интегрирования – интегрирование по частям.
Некоторые интегралы нельзя найти предыдущими способами, особенно при вычислении коэффициентов ряда Фурье. Поэтому необходим новый способ – интегрирование по частям. Чтобы этим способом решать, необходимо вывести формулу.
|
|
|
Пусть 
и 
– дифференцируемые функции аргумента . Известна формула производной произведения
или
,
откуда дифференциал произведения
.
Интегрируя обе части последнего равенства, получим
или
.
Отсюда
Полученное равенство называется формулой интегрирования по частям.
Пример 26. Найти 
.
Решение
Положим 
, 
.
Тогда 
, 
.
(Произвольное постоянное интегрирование напишем в окончательном результате).
Применяя формулу интегрирования по частям, имеем:
.
Пример 27. Найти 
.
Решение
Положим 
, 
.
Тогда 
, 
.
Применяя формулу интегрирования по частям, получим
.
Заметим, что для выбора множителей и 
нельзя дать общих указаний. Если положить 
и 
, то 
– интегрирование усложняется. Важно правильно сделать выбор множителей и .
Пример 28. Найти 
.
Решение
Положим 
, 
.
Тогда 
, 
.
Применяя формулу интегрирования по частям, получим:
.
Интеграл правой части равенства находим способом подстановки:
.
Находим
.
Таким образом,
.
Пример 29. Найти 
.
Решение
Положим , 
.
Тогда
, 
.
Применяя формулу интегрирования по частям, получим
.
Запись решения следует производить так:
.
Решить самостоятельно
Найти
1) 
Ответ: 
;
2) 
Ответ: 
.
Интегрирование в отличие от дифференцирования требует от решающего известной изобретательности и смекалки, что вырабатывается в процессе решения.
Если хотите лучше усвоить интегрирование, решайте больше примеров на интегрирование.
План 2005/2006, поз.
Гресюк Татьяна Казимировна
