Сравнения и классы вычетов по идеалу

Пусть - коммутативное кольцо, J - идеал этого кольца, тогда алгебра - подкольцо данного кольца, а значит сама является кольцом. По определению кольца, - аддитивная абелева группа, - ее подгруппа, причем, т.к. абелева, то - нормальный делитель этой группы. Следовательно, он определяет разбиение группы на непересекающиеся смежные классы по подгруппе .

В кольце эти смежные классы называются классами вычетов по идеалу J. Множество классов вычетов кольца по идеалу J будем обозначать K/J.

Пример

5.1. Пусть - кольцо целых чисел, J =(3), J=3Z.

Построим классы вычетов кольца по идеалу J=3Z.

2+3Z	…-1, 2, 5, 8, …
1+3Z	…-2, 1, 4, 7, …
3Z	…-3, 0, 3, 6, …

Z/3Z={3Z, 1+3Z, 2+3Z} – множество классов вычетов кольца по идеалу J=(3)=3Z.

Определение. Элементы a и b кольца называются сравнимыми по идеалу J, если .

Этот факт обозначают .

Например, в кольце для идеала J =(3)

, т.к. 19-4=15

Критерий сравнимости по идеалу

Для того чтобы два элемента кольца 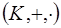были сравнимы по идеалу J данного кольца необходимо и достаточно, чтобы они принадлежали одному классу вычетов по идеалу J.

Фактор-кольцо

Рассмотрим множество классов вычетов кольца 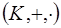по идеалу , т.е. множество смежных классов группы по подгруппе .

, где .

На этом множестве в I части была определена операция сложения классов и доказано , т.е. сложение есть алгебраическая операция на множестве .

Определим произведение классов вычетов по идеалу .

Определение. Произведением классов и назовем класс, в котором лежит произведение , т.е. .

Можно доказать, что наше определение не зависит от выбора элементов в классах , . Это означает, что операции умножения - алгебраическая на множестве .

Теорема. Алгебра является кольцом.

Это кольцо называется фактор-кольцом кольца 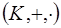по идеалу .

Примеры

5.2. Постройте фактор-кольцо кольца по идеалу . Составьте таблицы сложения и умножения классов.

Решение: Классы вычетов кольца по идеалу построены в примере 5.1. - множество классов вычетов кольца по идеалу ().

- фактор-кольцо кольца по идеалу .

Таблица сложения					Таблица умножения

Из таблицы видим: нулевой элемент - класс , противоположные элементы , , . Единичный элемент - класс .

5.3. Постройте фактор-кольцо кольца по идеалу . Составьте таблицы сложения и умножения классов.

Решение: . По определению главного идеала , , видим, что идеал состоит из целых чисел Гаусса с четными действительной частью и коэффициентом при мнимой части.

Разбиваем множество на попарно непересекающиеся классы по идеалу .

;

Класс вычетов состоит из целых чисел Гаусса с нечетной действительной частью и четным коэффициентом при мнимой части. Класс состоит из целых чисел Гаусса с четной действительной частью и нечетным коэффициентом при мнимой части. Наконец, класс состоит из целых чисел Гаусса с нечетными действительной частью и коэффициентом при мнимой части. Никаких других классов вычетов, которые были бы отличны от найденных, получить нельзя.