Для выяснения вопроса о существовании предела функции(числовой последовательности) использовать сформулированные выше определения, не всегда удобно. Бывает, что проще это сделать с помощью признаков существования пределов.
Теорема 5.4.1. (без доказательства). Если числовая последовательность 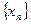 монотонная и ограниченная, то она имеет предел.
монотонная и ограниченная, то она имеет предел.
Эту теорему можно представить в виде:
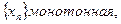
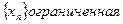 ,т.е. при
,т.е. при 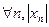 < М
< М 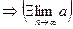
М>0
Возможны два случая:
1. последовательность монотонно возрастает, т.е. для 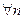 выполняются условия
выполняются условия 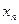 <
<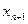 и ограниченна сверху, т.е.
и ограниченна сверху, т.е. 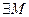 такая, что для любого п
такая, что для любого п 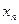 < M
< M
2. последовательность монотонно убывает и ограниченна снизу, т.е. 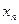 >
>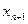 и для любого п
и для любого п > M.
> M.
Без доказательства продемонстрируем наличие предела на (рис.5.4.1)
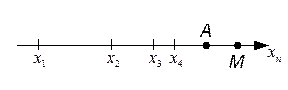
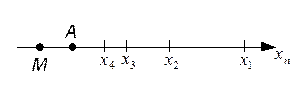
Рис.5.4.1
Можно показать (используя формулу бинома Ньютона), что и следующие члены последовательности для 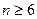 также возрастают, т.е. данная последовательность монотонно возрастает.
также возрастают, т.е. данная последовательность монотонно возрастает.
Из формулы бинома Ньютона следует также, что любой член последовательности меньше трех: 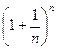 <3 т.е. последовательность
<3 т.е. последовательность 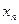 - ограниченна сверху. На основании теоремы 5.4.1 следует, что существует
- ограниченна сверху. На основании теоремы 5.4.1 следует, что существует 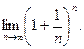 этот пределобозначается символом " е " и называется "числом е".
этот пределобозначается символом " е " и называется "числом е".
|
|
|
е (5.4.1)
(5.4.1)
Позже будет показано, что е =2,718281… является иррациональным числом.
"Число е "(число Эйлера, неперово число) играет весьма важную роль в математическом анализе. График функции у= е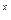 получил название экспоненты. Широко используются логарифмы по основанию е, называется натуральными. Натуральные логарифмы обозначаются символом:
получил название экспоненты. Широко используются логарифмы по основанию е, называется натуральными. Натуральные логарифмы обозначаются символом: 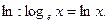 Между десятичными и натуральными логарифмами имеет место такая связь:
Между десятичными и натуральными логарифмами имеет место такая связь:  или
или 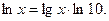
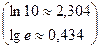
 2014-02-05
2014-02-05 1557
1557








