Рассчитаем коэффициенты регрессии и эластичности

Для рассматриваемого примера система нормальных уравнений будет выглядеть так:

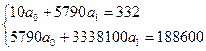(11)

Решая систему, получим следующее уравнение регрессии:

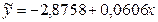(12)

Коэффициент регрессии в уравнении а₁=0,0606 показывает среднее увеличение суммы издержек обращения на 60,6 тыс. руб. на каждый миллион прироста товарооборота.

Коэффициент регрессии имеет большое практическое значение, например, в связи с прогнозированием поведения результативного показателя в зависимости от изменения фактора-признака.

Коэффициент регрессии также используется при определении показателя эластичности. Коэффициент эластичности Э характеризует процент изменения результативного показателя в случае изменения фактора-признака на один процент.

В рассмотренном примере можно говорить об эластичности издержек обращения по отношению к товарообороту. Часто говорят об эластичности спроса в зависимости от дохода и т.д.

Если имеется зависимость показателя у от х, то формула для определения эластичности показателя у такова:

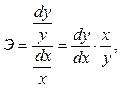(13)

В случае расчета показателя у по линейному уравнению регрессии формула (13) приобретает вид

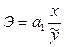(14)

т.е., чтобы получить коэффициент эластичности, например, спроса в зависимости от дохода, нужно коэффициент регрессии а₁ умножить на отношение

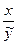(15)

где х – интересующее нас значение дохода, а 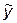- спрос, вычисленный по уравнению регрессии при данном доходе.

Коэффициент эластичности может быть вычислен для любого значения фактора-признака х=х₀. Можно найти также среднее значение коэффициента эластичности .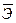

Найдем коэффициент эластичности издержек обращения у, воспользовавшись уравнением регрессии 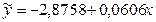(табл.4).

Таблица 4

Расчетная таблица

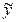
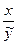
Товарооборот X	Расчетные издержки обращения		Коэффициент эластичности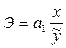
	26, 2122	18, 3120	1, 1097
	28, 0302	18, 1946	1, 1026
	29, 2422	18, 1244	1, 0983
	29, 8482	18, 0915	1, 0963
	31, 6662	18, 0002	1, 0908
	32, 8782	17, 9450	1, 0875
	34, 6962	17, 8693	1, 0829
	35, 9082	17, 8232	1, 0801
	36, 5142	17, 8012	1, 0788
	37, 1202	17, 7800	1, 0775
В среднем:	32, 2116	17, 9942	1, 0904

Средний коэффициент эластичности издержек обращения

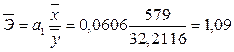
При увеличении товарооборота на 1% издержки обращения увеличиваются на 1,09%.

2.1.5. Проверка адекватности регрессионной модели

После построения регрессионной модели необходимо проверить ее на адекватность исследуемому процессу, т.е. необходимо выяснить, правильно ли она отображает зависимость исследуемого показателя y от показателя х.

Это нужно сделать для того, чтобы убедиться в пригодности и надежности модели для использования в прикладных целях, в частности для прогнозирования показателя у в будущем (экстраполяция) или в ретроспективном анализе (интерполяция или анализ прошлого). В проверке модели на адекватность большую роль играет не объясненная моделью дисперсия, или остаточная дисперсия 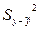(дисперсия остатков 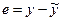), и объясненная дисперсия .

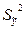Приведем формулу для проверки адекватности линейной модели 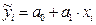. Линейная модель считается адекватной, если остаток 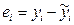является случайной величиной с нормальным законом распределения 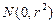остатков, (т.е. математическое ожидание остатков 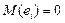) и дисперсия остатков .

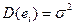В этом случае показатель F

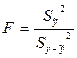, (16)

характеризующий отношение объясненной дисперсии к остаточной, подчиняется распределению Фишера с 1 и (n-2) степенями свободы.

Полученное значение F сравнивается с табличным значением F_т – распределения Фишера при заданной доверительной вероятности 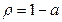(а – уровень значимости).

Уравнение регрессии считается значимым и может быть использовано в прикладных целях, если 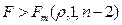. Если же 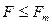, то уравнение не является достаточно надежным.

Если статистическая модель содержит к параметров, то показатель 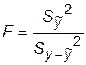сравнивается с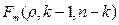

.

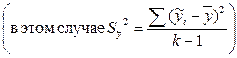где 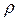- по-прежнему доверительная вероятность, а (к-1) и (n-к) – параметры F – распределения.

По виду расчетного показателя F можно судить о характере аппроксимации корреляционного поля линией регрессии. Чем меньше дисперсия остатков (необъясненная дисперсия) или же чем выше объясненная дисперсия, тем лучше линия регрессии по сравнению с другими опробованными линиями.

Для подбора подходящей модели можно пользоваться также корреляционным отношением, индексом корреляции или коэффициентом детерминации.

Чем ближе к единице эти показатели, тем лучше модель.

При компьютерной реализации выбор наиболее адекватной модели может осуществляться автоматически или же сопровождаться вычисленными значениями указанных показателей, необходимых для сравнения.

2.1.6. Прогнозирование с помощью уравнения регрессии

Уравнение регрессии после проверки его значимости можно использовать для предсказания значений результирующего показателя у при интересующих нас х, отличных от выборочных значений.

Если значение признака х=х₀ содержится в интервале (min x_i, max x_i), то речь идет об интерполяции, если же точка х₀ находится вне интервала – об экстраполяции или же собственно о прогнозировании с некоторым интервалом упреждения.

Прогноз значений исследуемого показателя может быть точечным, а может быть и интервальным.

Точечный прогноз осуществляется прямой подстановкой точки х₀ в уравнение регрессии, например линейное 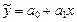. Значение 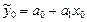- это и есть точечный прогноз показателя y. Так как вероятность попадания в любую точку равна нулю, то фактическое значение исследуемого показателя y при значении независимого показателя 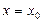никогда в точности не совпадет с точечным прогнозом 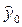, а будет находиться в некотором интервале, содержащем 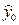. Поэтому практически важнее интервальный прогноз.

Границы этого интервала равноудалены от центра 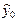и определяются на основе дисперсионного анализа.

Для определения доверительного интервала задаются некоторой доверительной вероятностью r прогноза, т.е. фактически задается надежность прогноза. Обычно доверительная вероятность задается равной 0,95 или же 0,90. Задача ставится так: требуется найти такой интервал, куда среднее значение прогнозируемого показателя, соответствующее точке 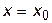попадет, например с вероятностью 0,95. Ответ на таким образом поставленный вопрос дает следующая формула:

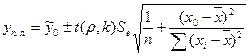(17)

где у_п, у_л – соответственно правая и левая границы интервала; n – объем выборки, на основе которой построено уравнение регрессии; к – число степеней свободы или количество неизвестных параметров в уравнении регрессии; 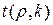- табличное значение параметра t статистики Стьюдента; S_e – стандартная ошибка уравнения регрессии .

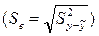Иногда вместо доверительной вероятности задают уровень значимости (а) или порог риска прогноза, т.е. вероятность того, что прогноз не попадет в интервал (17) (r =1-а).

Ясно, что большей надежности прогноза будет отвечать более широкий интервал; если требуется сделать прогноз с меньшей надежностью, то формула (17) дает интервал меньшей длины.

Из формула (17) видно, что при заданной доверительной вероятности самый узкий интервал получается при 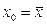, а чем дальше точка 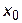будет отстоять от среднего значения 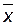, тем больше значение у для данного 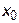. Другими словами, интерполяция вблизи точки 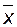даст хорошие результаты, а выход из области наблюдений, т.е. экстраполяция, приводит к худшим предсказаниям (рис. 7).

Рис 7. Доверительные интервалы при заданной вероятности r.

Иногда вместо задачи прогнозирования с требуемой надежностью прогноза рассматривается "обратная" задача: требуется указать надежность, с которой интересующее нас значение исследуемого показателя попадает в заданный интервал.

Выводы

Сформулируем в заключение методику построения модели парной корреляции кратко.

Этап 1. Подготовка данных.

Подбирается статистика для модели в виде точечных или интервальных рядов значений переменных Y и X. Строится корреляционное поле или эмпирическая линия регрессии.

Этап 2. Оценка тесноты связи между признаками.

2.1. По исходному ряду данных рассчитывается выборочный коэффициент корреляции r_xy, который измеряет тесноту линейной связи показателей.

Значение коэффициента парной корреляции лежит в интервале от –1 до +1. Положительное его значение свидетельствует о прямой связи, отрицательное – об обратной, т.е. когда растет одна переменная, другая уменьшается. Чем ближе его значение к единице, тем теснее связь. Считается, что связь достаточно сильная, если коэффициент корреляции по абсолютной величине превышает 0,7, и слабая, если он меньше 0,3.

Близкое к нулю значение коэффициента корреляции говорит об отсутствии линейной связи переменных, но не об отсутствии связи между ними вообще.

2.2. Существуют и универсальные показатели тесноты корреляционной связи: корреляционное отношение h_xy, индекс корреляции I_yx, коэффициент детерминации. Эти показатели подходят для измерения тесноты как линейной, так и любой нелинейной связи. В частности, для линейной модели r_xy=h_xy=I_yx. Однако для расчета любого из универсальных показателей необходима конкретная корреляционная модель, которую мы можем иметь лишь после этапов III (спецификация модели) и IV (параметризация модели). Поэтому расчет универсальных показателей проводят после этапов III и IV. В случае наличия сильной корреляционной связи правильно подобранная модель дает высокие значения универсальных показателей.