Типовые звенья АСР

Автоматические системы регулирования состоят из элементов раз­личной сложности. Многие из них могут быть разделены на более про­стые звенья. При этом звенья должны обладать детектирующими свой­ствами и их динамические свойства должны описываться простейшими алгебраическими и дифференциальными уравнениями. Звенья, обла­дающие такими свойствами, принято называть типовыми. Они имеют определенные названия в соответствии с их функциональными свойст­вами. Любой элемент системы может быть представлен в виде комби­нации типовых звеньев. Они легко технически реализуются, что позволяет создавать устройства с заданными свойствами.

Свойства усилительного (безынерционного статического) звена описываются алгебраическим уравнением

где k коэффициент усиления (пропорциональности, передачи) звена. Передаточная и переходная функции звена:

Пропорциональное звено изменяет входной сигнал по модулю в k раз.

Примеры усилительного звена: рычажные передачи, пружины, мембраны, сильфоны, усилители и т. д.

Свойства интегрирующего звена описываются уравнением

где k _и - коэффициент передачи, определяющий скорость интегрирования; k _и = tgoc(рис. 8.16).

Передаточная и переходная функции звена:

Выходная величина изменяется с постоянной скоростью пропорционально величине коэффициента k _и.

Примеры интегрирующего звена: сервоприводы гидравлические; сосуд, жидкость из которого откачивается насосом; интегральный регулятор и т. д.

Свойства апериодического (инерционного) звена первого порядка описываются обыкновенным дифференциальным уравнением

где T - постоянная времени, имеющая размерность времени.

Передаточная функция звена

Переходную функцию звена можно получить, воспользовавшись таблицей соответствия (табл. 8.1, пятая строка):

Подставив в выражение (8.56) значения параметров, можно рас­считать ординаты переходного процесса для дискретных значений вре­мени и построить график (рис. 8.17). Постоянная времени T определяет угол наклона касательной, проведенной из начала координат, а коэффи­циент пропорциональности k определяет установившееся значение вы­ходного параметра при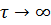

Уравнением апериодического зве­на первого порядка описываются эле­менты, имеющие одну ёмкость для на­копления массы или энергии. К ним от­носятся ранее рассмотренные сосуд со свободным сливом и теплообменник смешения.

Свойства идеального дифферен­цирующего звена описываются уравнением

где k _д - коэффициент пропорциональности, называемый временем

дифференцирования.

Передаточная и переходная функции звена

Из выражения (8.57) следует, что выходная величина идеального дифференцирующего звена пропорциональна скорости изменения входного сигнала. Если на вход такого звена подать единичный ступен­чатый сигнал 1(т), то за бесконечно малый промежуток времени вы­ходная величина h(x) = k_д ◦ 1(τ) должна достигнуть бесконечности и

вернуться к нулевому значению (8.59). Физически реализовать такое звено не представляется возможным, так как порядок правой части уравнения m = 1 больше порядка левой части n = 0. Поэтому для вы­полнения операций дифференцирования сигналов используют реаль­ные дифференцирующие звенья, свойства которых описываются урав­нением

Передаточная функция звена имеет вид

Для получения выражения переходной функции запишем решение в операторной форме и применим к нему операцию обратного преобра-зования Лапласа:

Выходной сигнал (рис. 8.18) в момент τ = 0 увеличивается в k раз и плавно уменьшается до нуля. Для приближения свойств реального дифференцирующего звена к свойствам идеального звена необходимо одновременно увеличивать коэффициент пе­редачи k и уменьшать постоянную времени T так, чтобы их произведение kT = k _д остава­лось постоянным.

Реальные дифференцирующие звенья, выполненные из элементов аналоговой и цифровой техники, используются для выпол­нения операции дифференцирования медлен­но меняющихся процессов и создания коррек­тирующих устройств в АСР.

Свойства апериодических и колебательных звеньев второго по­рядка описываются обыкновенным дифференциальным уравнением второго порядка

где T ₁ и T ₂ - постоянные времени.

Значения коэффициентов дифференциального уравнения (8.63) и корней его характеристического уравнения оп­ределяют свойства и характер переходного процесса.

1. Если выполняется условие , то корни характеристического уравнения будут простые: p ₁ = -0₁; p₂ = -а₂

Переходная функция имеет апериодический характер, поэто­му звено называется апериодическим второго порядка. Оно не относится к типовым звеньям, так как структурно, в соответствии с переда-точной функцией, его можно представить в виде последовательного со-единения двух апериодических звеньев:

2. Если выполняется условие , то корни характеристического уравнения будут комплексными сопряженными: p₁=-а + i 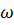и p₂ = -а - i .

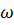В связи с тем, что в выражении (8.67) содержатся периодические функции си­нус и косинус, то переходный процесс становится колебательным (рис. 8.19). Скорость затухания колебаний зависит от модуля вещественной составляющей а корней характеристического уравнения (8.64), находящейся в показателе экспо­ненты.

Колебательность переходного процесса обычно оценивают по степени затухания:

Колебательность переходного процесса можно оценить и по кор­невому показателю колебательности m, равному модулю отношения вещественной части корней а к мнимой части :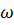

Его можно выразить через коэффициенты дифференциального уравнения (8.63), подставив соответствующие выражения а и :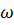

Учитывая, что получим выражение, свя­зывающее степень затухания с корневым показателем колебательности,

Приведем значения m и T ₁ / T ₂, соответствующие наиболее часто употребляемым значениям степени затухания:

С увеличением степени затухания процесса растет корневой пока­затель колебательности m и отношение постоянных времени T ₁ /T₂.

3. Если выполняется условие то характеристическое уравнение будет иметь кратные вещественные корни p₁ = p₂=-а.

Этому условию будет соответствовать переходная характеристика

Переходный процесс будет апериодический (см. рис. 8.13).

4. Если T ₁ = 0, то динамические свойства звена будут описываться уравнением

Характеристическое уравнение T ₂² p² + 1 = 0 будет иметь кратные

1 чисто мнимые корни . Этому условию будет соответство­вать переходная характеристика

Переходная характеристика звена со-держит незатухающие колебания (рис. 8.20). Такое звено называется консервативным.

В качестве примера консервативного звена можно назвать центробежный маят-ник, используемый в качестве регулятора частоты вращения вала паровой машины, без демпфера.

Свойства звена «чистого запаздывания» описываются уравнением

Передаточная функция –

Переходная функция –

Звено «чистого запаздывания» не деформирует входной сигнал, а только задерживает его появление на выходе на величину времени запаздывания τ₀.

Запаздывание в передаче сигнала возникает в связи с ограниченной скоростью прохождения сигнала через физические элементы.