Пусть в группе  взята произвольная подгруппа
взята произвольная подгруппа  .
.  ,
,  .
.
Определение. Подгруппа  группы
группы  называется нормальным делителем этой группы, если левостороннее разложение группы
называется нормальным делителем этой группы, если левостороннее разложение группы  по подгруппе
по подгруппе  совпадает с правосторонним..
совпадает с правосторонним..
| … | … | |||

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
|
Левостороннее разложение группы  по подгруппе
по подгруппе  состоит из классов
состоит из классов  ,
,  ,
,  , …
, …
Правостороннее – из классов  ,
,  ,
,  , …
, …
Отсюда видим, что определению нормального делителя можно придать такую форму:
Определение. Подгруппа  группы
группы  называется нормальным делителем этой группы, если для любого
называется нормальным делителем этой группы, если для любого 
 .
.
Примеры
Из определения следует, что все подгруппы абелевой группы являются в ней нормальными делителями. Во всякой группе  и единичная подгруппа, и сама группа будут нормальными делителями: оба разложения группы
и единичная подгруппа, и сама группа будут нормальными делителями: оба разложения группы  по единичной подгруппе совпадают с разложением группы на отдельные элементы, оба разложения группы
по единичной подгруппе совпадают с разложением группы на отдельные элементы, оба разложения группы  по самой этой группе состоят из одного класса
по самой этой группе состоят из одного класса  .
.
В примерах 3.1, 3.2, 3.3, 3.4 §3 группы являются абелевыми, значит, каждая подгруппа является нормальным делителем. В примере 3.5 а левостороннее и правостороннее разложения группы  по подгруппе
по подгруппе  не совпадают, следовательно, подгруппа
не совпадают, следовательно, подгруппа  нормальным делителем группы
нормальным делителем группы  не является.
не является.
В примере 3.5 б знакопеременная подгруппа  является нормальным делителем группы
является нормальным делителем группы  , так как левостороннее разложение группы
, так как левостороннее разложение группы  по подгруппе
по подгруппе  совпадает с правосторонним.
совпадает с правосторонним.
Фактор-группы
Пусть дана группа  и
и  - ее нормальный делитель. Он разбивает группу на непересекающиеся левые (правые) смежные классы, причем левые и правые смежные классы можно не различать.
- ее нормальный делитель. Он разбивает группу на непересекающиеся левые (правые) смежные классы, причем левые и правые смежные классы можно не различать.
| … | ||

| 
| |

| 
| |

| 
| , |
где  .
.
Множество всех смежных классов группы  по подгруппе
по подгруппе  обозначим
обозначим  .
.
Определим на этом множестве произведение классов.
Определение. Произведением классов  и
и  называется множество
называется множество  .
.
Теорема. Произведение любых двух смежных классов группы  по подгруппе
по подгруппе  есть смежный класс, причем
есть смежный класс, причем  .
.
Из теоремы следует, что умножение есть алгебраическая операция на множестве  , тогда можно доказать, что алгебра
, тогда можно доказать, что алгебра  является группой.
является группой.
Определение. Алгебра  называется фактор-группой группы
называется фактор-группой группы  по нормальному делителю
по нормальному делителю  .
.
Примеры
4.4. Пусть  аддитивная группа целых чисел,
аддитивная группа целых чисел,  – подгруппа чисел, кратных 3, являющаяся нормальным делителем данной группы. Разобьем группу
– подгруппа чисел, кратных 3, являющаяся нормальным делителем данной группы. Разобьем группу  с помощью подгруппы
с помощью подгруппы  на попарно непересекающиеся смежные классы.
на попарно непересекающиеся смежные классы.

| …-1,2,5,8,11,… |

| …-2,1,4,7,10,… |

| …-3,0,3,6,9,… |
 .
.
 – фактор-группа группы
– фактор-группа группы  по подгруппе
по подгруппе  .
.
Найдем, например, сумму классов  и
и  . По теореме о сумме классов в аддитивной фактор-группе
. По теореме о сумме классов в аддитивной фактор-группе

 .
.
Аналогично находится сумма любых других классов фактор-группы  .
.
Составим таблицу сложения классов.

| 
| 
| |

| 
| 
| 
|

| 
| 
| 
|

| 
| 
| 
|
Из таблицы видим, что операция сложения классов коммутативна. Нулевой элемент – класс  . Противоположный элемент для каждого класса равен
. Противоположный элемент для каждого класса равен  ,
,  ,
,  .
.
4.5 Пусть  – мультипликативная группа корней 6-ой степени из 1,
– мультипликативная группа корней 6-ой степени из 1,  – подгруппа корней квадратных из 1, нормальный делитель данной группы.
– подгруппа корней квадратных из 1, нормальный делитель данной группы.
В примере 3.5 построены попарно непересекающиеся смежные классы группы  по подгруппе
по подгруппе 

| 
|

| 
|

| 
|
 .
.
 фактор-группа группы
фактор-группа группы  по подгруппе
по подгруппе  .
.
Найдем произведение, например, классов  и
и  . По теореме о произведении классов в мультипликативной фактор-группе
. По теореме о произведении классов в мультипликативной фактор-группе
 , так как
, так как  , то
, то  (по свойству 1 смежных классов). Следовательно,
(по свойству 1 смежных классов). Следовательно,  .
.
Таблица Кэли для фактор-группы 

| 
| 
| |

| Н | 
| 
|

| 
| 
| 
|

| 
| 
| 
|
Из таблицы видим, что операция умножения классов коммутативна. Единичный элемент – класс  . Обратный элемент для каждого класса равен
. Обратный элемент для каждого класса равен
 ,
,  ,
,  .
.
4.6. Пусть дана симметрическая группа 3-ей степени  и
и 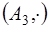 ее подгруппа четных подстановок, являющаяся нормальным делителем данной группы (Пример 3.5 б).
ее подгруппа четных подстановок, являющаяся нормальным делителем данной группы (Пример 3.5 б).
В этом примере построены попарно непересекающиеся смежные классы группы  по подгруппе
по подгруппе 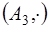 :
:

| 
|

| 
|

 – фактор-группа группы
– фактор-группа группы  по подгруппе
по подгруппе 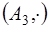 .
.
Найдем, например, произведение классов  и
и  . По теореме о произведении классов в мультипликативной фактор-группе
. По теореме о произведении классов в мультипликативной фактор-группе
 (Использовали таблицу Кэли примера 1.10).
(Использовали таблицу Кэли примера 1.10).
Таблица умножения классов фактор-группы 
| × | 
| 
|

| А3 | 
|

| 
| 
|
Из таблицы видим, что операция умножения классов коммутативна. Единичный элемент – класс  . Обратный элемент для каждого класса
. Обратный элемент для каждого класса
 ,
,  .
.
 2020-04-12
2020-04-12 2483
2483
