Основные свойства тройного интеграла
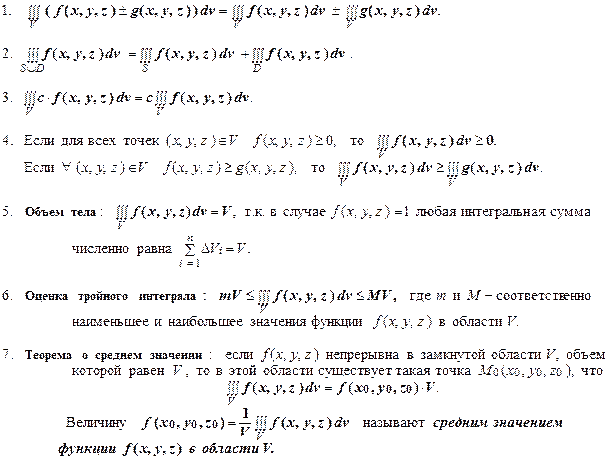
Тройной интеграл обладает теми же свойствами, что и двойной интеграл:
Вычисление тройного интеграла сводится к последовательному вычислению трех











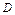
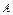
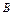
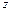
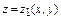
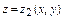 определенных интегралов.
определенных интегралов.
Пусть область интегрирования V – тело, ограниченное снизу
поверхностью z = z 1(x, y), сверху - поверхностью z = z 2(x, y),
причем z 1(x, y), z 2(x, y) (z 1(x, y) £ z 2(x, y)) – непрерывные
функции в замкнутой области D, являющейся проекцией тела на
плоскость Оху (рис. 1).
Считаем, что область V правильная в направлении оси Oz: любая
прямая, параллельная оси Oz, пересекает границу области не более
чем в двух точках (или по целому отрезку). Тогда для любой
непрерывной в области V функции f (x, y, z) имеет место формула Рис. 1.












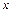
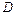
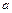
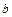
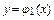
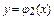
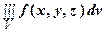 =
= 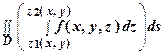 , (2)
, (2)
сводящая вычисление тройного интеграла к вычислению двойного
интеграла от однократного. При этом сначала вычисляется внутренний
интеграл по переменной z, при постоянных х и у в пределах измене-
ния z. Нижней границей интеграла является аппликата точки А – точки
входа прямой, параллельной оси Oz, в область V, т.е. z = z 1(x, y); верхней
|
|
|
границей – аппликата точки В – точки выхода прямой из области V,
т.е. z = z 2(x, y). Результатом вычисления этого интеграла является Рис.2.
функция двух переменных х и у.
Если область D ограничена линиями х = а, х = b (a < b), y = j 1(x) и y = j 2(x), где j 1(x) и j 2(x) – непрерывные на отрезке [ a, b ] функции, причем j 1(x) £ j 2(x) (рис. 2), то, переходя от двойного интеграла по области D к повторному, получаем формулу, по которой вычисляется тройной интеграл в декартовых координатах:
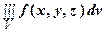 =
= 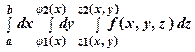 , (3)
, (3)
Пример 1. Пусть V – тело, ограниченное эллипсоидом 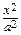 +
+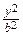 +
+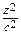 = 1.
= 1.
В этом случае D состоит из точек, удовлетворяющих неравенству 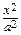 +
+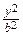 ≤ 1 =>
≤ 1 =>
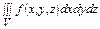 =
=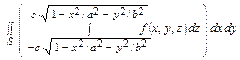 =
=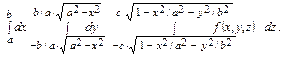
Замечания. 1. Если область V представляет собой прямоугольный параллелепипед
V ={ a £ x £ b, c £ y £ d, l £ z £ m }, проектирующийся на плоскость Oyz в прямоугольник
R ={ c £ y £ d, l £ z £ m }. Тогда
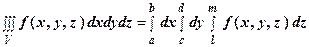 .
.
2. Если область V более сложная, чем рассмотренная, то ее следует разбить на конечное число таких областей (правильных), к которым можно применить формулу (3).
3. Порядок интегрирования в формулах (3)- (4), при определенных условиях,
может быть иным.
Пример 2. Найти объем тетраэдра, ограниченного плоскостями: х = 0, у = 0, z = 0 и x + 2 y + z – 6 = 0.


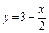







 Проекцией тетраэдра на плоскость Оху является треугольник, образованный прямыми
Проекцией тетраэдра на плоскость Оху является треугольник, образованный прямыми
х = 0, у = 0 и x + 2 y = 6, т.е. х изменяется от 0 до 6, а при фиксированном х (0 ≤ х ≤ 6)
у изменяется от 0 до 3 –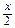 (рис. 3). Если же фиксировать и х и у, то точка может
(рис. 3). Если же фиксировать и х и у, то точка может
перемещаться по вертикали от плоскости z = 0 до плоскости x + 2 y + z – 6 = 0, т.е.
меняется в пределах от z = 0 до z = 6 – х – 2 у. Следовательно,
V =|| f (x, y) = 1 || = 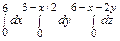 =
= 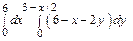 =
= 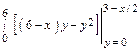 dx = Рис.3.
dx = Рис.3.
|
|
|
= 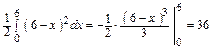 .
.
 2014-02-12
2014-02-12 869
869








